
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нельзя путать отношения объемов и отношения часть – целое!
Важно: объем единичных понятий либо целиком входит в объем другого понятия, либо целиком из него исключается. Пересечения объемов здесь быть не может!
Нельзя путать отношения объемов и отношения часть – целое!
1 шаг. Определяем какое отношение между понятиями А и В – совместимое или нет. Для этого задаем вопрос: может ли А быть В, а В быть А. Если в каком-то смысле А может быть В, и наоборот, то перед нами отношения совместимости. Если же нет, то несовместимость.
2 шаг. Если отношение между А и В совместимое, то устанавливаем вид совместимости.
 Если все А есть В, и все В есть А, то мы имеем ранообъемность(равнозначность).
Если все А есть В, и все В есть А, то мы имеем ранообъемность(равнозначность).
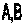
Если некоторые А есть В, а некоторые В есть А, то отношение пересечения.

 |

 |
Если все А есть В, а некоторые В есть А, то у нас отношение подчинения понятия А понятию В. Объем понятия А целиком входит в объем понятия В, но объем понятия В шире объема понятия А. .
 |
3 шаг. Если отношение между А и В – несовместимое, то устанавливаем вид несовместимости.


 Если понятия А и В есть виды одного рода, или просто совершенно разные вещи, то у нас будет внеположность(исключение).
Если понятия А и В есть виды одного рода, или просто совершенно разные вещи, то у нас будет внеположность(исключение).
 |
 Если это противоположные понятия, между которыми есть промежуточные звенья, то это отношение противоположности
Если это противоположные понятия, между которыми есть промежуточные звенья, то это отношение противоположности
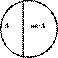 Если это положительное и отрицательное понятие одного и того же объекта, то отношение противоречия:
Если это положительное и отрицательное понятие одного и того же объекта, то отношение противоречия:
4 шаг. Изображаем отношение между А и В графически.
5 шаг. Аналогично действуем, если у нас три понятия: рассматриваем отношение А к В, отношение А к С и отношение В к С и изображаем графически соотношение их объемов. И также, если понятий у нас больше, чем три.
Образец.
Дано: Определить отношения между понятиями: небо, голубое, цветное и изобразить их с помощью кругов Эйлера.
1шаг. Определяем отношение между понятиями «небо» и «голубой». Небо может быть голубым, а может и не быть. Голубое может быть небом, а может и не быть. Значит, между «голубым» и «небом» у нас отношение совместимости.
2 шаг. Определяем, какой вид совместимости есть между этими понятиями: это пересечение.
3 шаг Изображаем это отношение графически:
 |
4 шаг. Определяем отношение между понятиями «голубое» и «цветное». Всякое голубое етсь цветное, но не всякое цветное есть голубое. Значит, у нас отношение совместимости.
5 шаг. Определяем вид совместимости. Очевидно, это отношение подчинения, «голубое» подчинено «цветному», «цветное» выступает как род, а «голубое» как вид.
6 шаг. Изображаем графически:
 |

 7 шаг. Определяем отношение понятий «небо» и «цветное». Небо может быть цветным, а может и не быть. И цветное может быть небом, а может быть чем-то другим. Значит, у нас опять отношение пересечения.
7 шаг. Определяем отношение понятий «небо» и «цветное». Небо может быть цветным, а может и не быть. И цветное может быть небом, а может быть чем-то другим. Значит, у нас опять отношение пересечения.
 | |||
 | |||
8 шаг. Теперь нам осталось соединить вместе три отношения и изобразить их графически:
 |
В дальнейшем, если предстоит изобразить отношения объемов трех и более понятий, попарные их соотношения можно определять в уме, мысленно, а записывать лишь общий итог.
2. ОПРЕДЕЛЕНИЕ ПРАВИЛЬНОСТИ ОБОБЩЕНИЯ ИЛИ ОГРАНИЧЕНИЯ ПОНЯТИЙ
Обобщение – это логическая операция, идущая от вида к роду, а ограничение – логическая операция, идущая от рода к виду. В данном случае мы имеем дело с отношением подчинения между объемами понятий.
ПРОВЕРКА ОБОБЩЕНИЯ
1 шаг. Задаем вопрос: является ли понятие А родом для понятия В, или нет? Или: является ли понятие В видом понятия А или нет?
2 шаг. Если является, то обобщение правильно. Если нет, то неправильно.
3 шаг. Запишем полученный результат. Если обобщение неправильно, пишем, что понятие В не может быть видом понятия А.
4. шаг. Исправляем обобщение – подбираем правильное родовое понятие.
ПРОВЕРКА ОГРАНИЧЕНИЯ
1 шаг. Задаем вопрос: является ли понятие В видом понятия А или нет? Или: является ли понятие А родом для понятия В, или нет?
2 шаг. Если является, то ограничение правильно. Если нет, то неправильно.
3 шаг. Запишем полученный результат. Если ограничение неправильно, пишем, что понятие В не может быть видом понятия А.
4. шаг. Исправляем обобщение – подбираем правильное видовое понятие.
ОБРАЗЕЦ ДЛЯ ОБОБЩЕНИЯ:
Дано: обобщение понятия «динозавр». Динозавр – пресмыкающееся – земноводное.
1 шаг. Задаем вопрос: является ли динозавр видом пресмыкающихся, а пресмыкающиеся родом для динозавра? Ответ положительный. Значит, в данном случае обобщение правильное.
2 шаг. Задаем вопрос: является ли пресмыкающееся видом земноводного, а земноводное родом для пресмыкающегося? Ответ: нет, не является.
3 шаг. Запишем результат: земноводное не является родом для пресмыкающегося, поэтому обобщение неправильное.
4 шаг. Исправляем обобщение: динозавр – пресмыкающееся – живое существо.
ОБРАЗЕЦ ДЛЯ ОГРАНИЧЕНИЯ:
Дано: ограничение понятия «левый политик». Левый политик» - социалист – либерал.
1 шаг. Задаем вопрос: является ли социалист видом левого политика, а левый политик родом для социалиста? Да, является. Здесь ограничение правильно.
2 шаг. Задаем вопрос: является ли либерал видом социалиста, а социалист родом для либерала? Нет, не является.
3 шаг. Запишем: ограничение неправильно, так как либерал не является видом социалиста
4 шаг. Исправляем ограничение: левый политик – социалист – российский социалист.
3. ФОРМУЛИРОВАНИЕ ОПРЕДЕЛЕНИЯ ПОНЯТИЯ ЧЕРЕЗ РОД И ВИДОВОЕ ОТЛИЧИЕ
Определение раскрывает существенные признаки предмета, раскрывает содержание понятия. распространенным видом определения является определение через род и видовое отличие. Формула определения: Х есть Р(род)+видовые отличия(отличия от других видов того же самого рода). Не следует путать операцию определения с обобщением и ограничением понятия. Это – разные вещи.
1 шаг. Определяем ближайший род для данного понятия. По отношению к этому роду наше понятие будет видом. Записываем: Х есть Р(род).
2 шаг. Определяем, какие еще виды есть у этого рода.
3 шаг. Определяем, чем отличается наш вид, наше понятие от других видов внутри ЭТОГО же рода. Так мы находим видовые отличия. Можно воспользоваться помощью словаря.
4 шаг. Соединяем род и видовое отличие в одно высказывание и записываем его.
5 шаг. Проверяем наше определение на наличие ошибок.
Образец. Задание: дать определение понятию «ножницы».
1 шаг. Находим ближайший род. Ножницы – это инструмент. Но это еще не ближайший род. Ближайший род – это «режущий инструмент». Записываем: ножницы есть режущий инструмент.
2 шаг. Смотрим, какие еще бывают режущие инструменты: нож, резец, сверло, фреза, напильник.
3 шаг. Устанавливаем, какие признаки присущи именно ножницам и не присущи другим видам режущего инструмента. Это наличие двух раздвигающихся лезвий.
4 шаг. Формулируем наше определение: ножницы есть режущий инструмент с двумя раздвигающимися лезвиями.
5 шаг. Проверяем определение на ошибки.
4 ПРОВЕРКА ПРАВИЛЬНОСТИ ОПРЕДЕЛЕНИЯ
1 шаг. Определяем, что является определяющим, а что определяемым.
2 шаг. Смотрим правила определения и проверяем, не нарушены ли эти правила.
А) В первую очередь проверяем, не нарушено ли правило соразмерности определяемого и определяющего. Для этого поменяем местами определяемое и определяющее и подставим к определению сначала слово «все» или «каждый», затем слов «только». Если смысл не изменится, то определение правильно. Если при подстановке слова «все» обнаруживается неправильность, то имеет место ошибка «слишком широкое определение», если неправильность обнаруживается при подстановке слова «только», то у нас ошибка «слишком узкое определение».
Б) Проверяем наше определение по всем правилам. Находим ошибки, записываем: нарушено такое-то правило определения, гласящее, что… Записываем название ошибки(если таковое имеется).
3. Исправляем ошибки. Записываем правильное определение.
Образец. Дано определение: арбуз – это ягода.
1 шаг. Выявляем определяемое: это – арбуз. Выявляем определяющее – это ягода.
2 шаг.
А) Проверяем определение на нарушение правила равнозначности определяемого и определяющего. Меняем определяющее и определяемое местами и подставляем слово «все». Получаем: Всякая ягода есть арбуз. Ясно, что это неверно. Записываем: нарушено, гласящее, что определяемое и определяющее должны быть равнообъемными понятиями. Ошибка: «слишком широкое определение».
Б) Поверяем нарушение других правил определения. Других нарушений нет.
3 шаг. Исправляем наше определение.
Арбуз есть ягода, с красной мякотью, плодом шаровидной формы, заключенным в зеленую корку.
5 ПРОВЕРКА ДЕЛЕНИЯ НА НАЛИЧИЕ ОШИБОК
1 шаг. Устанавливаем структуру деления. Определяем, что является делимым, что основанием(критерием) деления, что членами деления. Записываем, что мы установили.
2 шаг. Проверяем деление на наличие ошибок. Для этого смотрим, какие правила деления нарушены. Прежде всего, обращаем внимание на то, выдерживается ли одно основание деления.
3 шаг. Записываем, какие нарушения правил нами найдены и названия ошибок (если они есть).
4 шаг. Исправляем деление и записываем, что получилось.
Образец. Дано деление: Все кошки делятся на кошек черного окраса, кошек красного окраса и длинношерстных.
1 шаг. Выявляем структуру нашего деления. Делимое: кошки. Члены деления: черного окраса, красного окраса, длинношерстные. Основание деления: а) окрас, б) длина шерсти.
2 шаг. Определяем, какие правила деления нарушены.
3 шаг. Записываем эти нарушения. нарушено правило, гласящее, что деление должно производиться по одному основанию. Ошибка: «подмена основания». Нарушено правило соразмерности, поэтому есть лишний член деления: «длинношерстные».
4 шаг. Исправляем деление и записываем результат: Все кошки делятся на кошек черного окраса и кошек красного окраса.
СУЖДЕНИЕ
1. ВЫРАЖЕНИЕ ВЫСКАЗЫВАНИЯ В ВИДЕ ЯВНОГО СУЖДЕНИЯ С КВАНТОРОМ И ЛОГИЧЕСКОЙ СВЯЗКОЙ И ОПРЕДЛЕНИЕ ЕГО ВИДА
Для того чтобы производить логические операции с суждением, его нужно выразить в явной форме, с квантором и связкой.
1 шаг. Определяем, что у нас субъект (S), что предикат (Р). Выписываем их.
2 шаг. Определяем связку. Если суждение утвердительное, то ставим связку «есть», если отрицательное, то ставим связку «не есть».
3 шаг. Определяем квантор. Есть только три квантора: для частных суждений квантор - «некоторые», для общеутвердительных – «все», для общеотрицательных – «ни одно».
4 шаг. Выписываем суждение с квантором и связкой.
5 шаг. Определяем его вид.
Всего существует 4 вида суждений:
Общеутвердительное: Все S есть Р. – обозначается буквой А.
Общеотрицательное: Ни одно S не есть Р. – обозначается буквой Е.
Частноутвердительное: Некоторые S есть Р. – обозначается буквой I.
Частноотрицательное: Некоторые не S есть Р. – обозначается буквой О.
6 шаг. Если суждение единичное, то оно считается за общее. Утвердительное единичное = общеутвердительное суждение – обозначается буквой А. Отрицательное единичное = общеотрицательное суждение – обозначается буквой Е.
Образец:
Исходное предложение: «Дружба – великая сила»
1 шаг. Определяем субъект и предикат. В нашем случае субъект(S) – «дружба», предикат (Р) – «великая сила».
2 шаг. Определяем связку. В данном случае суждение утвердительное. Значит, подходит связка «есть». Получаем: «Дружба есть великая сила».
3 шаг. Определяем квантор. Очевидно, здесь имеется виду всякая дружба. Значит, используем квантор «все». Его можно немного видоизменить – в данном случае можно использовать слово «всякий».
4 шаг. Выписываем: «Всякая дружба есть великая сила».
5 шаг. Раз у нас квантор «все» и связка «есть», то суждение общеутвердительное. Обозначается буквой А. Так и запишем.
2 ПОДБОР К ДАННОМУ СУЖДЕНИЮ ДРУГОГО СУЖДЕНИЯ В ЗАВИСИМОСТИ ОТ
ТИПА ОТНОШЕНИЙ МЕЖДУ НИМИ
Всего существует 4 типа отношений между суждениями(из них два с двумя вариантами). Субъект и предикат – одни и те же.
ПОДЧИНЕНИЕ: а) между общеутвердительным и частноутвердительным – между А и I, б) между общеотрицательным и честно отрицательным – между Е и О.
ПРОТИВОРЕЧИЕ: а) между общеутвердительным и частноотрицательным – между А и О, б) между общеотрицательным и частноутвердительным – между Е и I.
ПРОТИВОПОЛОЖНОСТЬ (КОНТРАРНОСТЬ): между общеутвердительным и общеотрицательным – между А и Е.
СУБКОНТРАРНОСТЬ: между частноутвердительным и частноотрицательным – между I и О.
1 шаг. Выражаем суждение в явной форме – с квантором и связкой.
2 шаг. Определяем его вид
3 шаг. Смотрим, в каком отношении наше суждение должно находиться к другому(субъект и предикат те же!).
4 шаг. Определяем вид этого другого суждения.
5 шаг. выписываем его формулу.
6 шаг. Выписываем нужное нам суждение, исходя из его формулы, но с нашими субъектом и предикатом.
Образец:
Исходное суждение: «Смерть – причина перемен»
1 шаг. Выражаем суждение в явной форме – с квантором и связкой. Получаем: «Всякая смерть есть причина перемен».
2 шаг. Определяем его вид. В данном случае суждение общеутвердительное(А).
3 шаг. Нужно отношение дано в задании. Пусть это будет отношение подчинения. Смотрим подчинение. Оно должно быть между А и I – между общеутвердительным и частноутвердительным.
4 шаг. У нас есть общеутвердительное. Значит, другое суждение должно быть частноутвердительным.
5 шаг. Формула частноутвердительного суждения: Некоторые S есть Р.
6 шаг. Брем эту формулу и применяем к нашим субъекту (смерть) и предикату (причина перемен). Получаем: «Некоторая смерть есть причина перемен».
3 ВЫВОДЫ ПО ЛОГИЧЕСКОМУ КВАДРАТУ
Логический квадрат выражает в графической форме все возможные отношения между суждениями, у которых одни и те же субъект и предикат.
Всего возможны четыре суждения с одними теми же субъектом и предикатом:
Общеутвердительное: Все S есть Р. – обозначается буквой А.
Общеотрицательное: Ни одно S не есть Р. – обозначается буквой Е.
Частноутвердительное: Некоторые S есть Р. – обозначается буквой I.
Частноотрицательное: Некоторые не S есть Р. – обозначается буквой О.
Для того чтобы сделать выводы по логическому квадрату, необходимо фиксировать исходное суждение и его истинность или ложность.
1 шаг. Выразить суждение в явной форме – с квантором и связкой.
2 шаг. Определить, истинно оно или ложно.
3 шаг. Выписать все четыре возможных суждения с данным субъектом и предикатом. Поставить истинность или ложность (в скобочках) после исходного суждения.
4 шаг. Руководствуясь логическим квадратом, и правилами конкретных отношений между суждениями нужно определить истинность или ложность других суждений с теми же субъектом и предикатом.
5 шаг. Пишем ответ.
Образец.
Дано: «Жалость – это имитация любви»
1 шаг. Выражаем с квантором и связкой: «Всякая жалость есть имитация любви».
2 шаг. Дано: суждение истинно.
3 шаг. Выписываем четыре суждения:
А) Всякая жалость есть имитация любви.(истинно)
I) Некоторая жалость есть имитация любви.
Е) Ни одна жалость не есть имитация любви.
О) Некоторая жалость не есть имитация любви.
4 шаг. Берем правила отношений между понятиями. Между А и I – подчинение. По правилу подчинения, если А – истинно, то I – тоже истинно. Значит, «Некоторая жалость есть имитация любви» - истинно. Между А и Е – противоположность. По правилу противоположности, если А – истинно, то Е – ложно. Значит, «Ни одна жалость не есть имитация любви». – ложно. Между А и О – противоречие. По правилу противоречия, если А – истинно, то О обязательно ложно. Значит, «Некоторая жалость не есть имитация любви». - ложно.
5 шаг. Пишем ответ:
А) Всякая жалость есть имитация любви.(истинно)
I) Некоторая жалость есть имитация любви.(истинно)
Е) Ни одна жалость не есть имитация любви. (ложно)
О) Некоторая жалость не есть имитация любви.(ложно)
Важно заметить, что иногда не удается установить истинность или ложность суждения. Тогда ответ будет: «неопределенно». Так, например, если исходное А у нас будет ложным. Тогда по правилу противоположности мы не сможем установить будет ли Е истинным или ложным. Аналогично и с I. Такое бывает и в тех случаях, когда исходным суждением является частное суждение.
4 ВЫРАЖЕНИЕ СЛОЖНОГО СУЖДЕНИЯ В СИМВОЛИЧЕСКОЙ ФОРМЕ
Сложное суждение состоит из нескольких простых суждений, связанных логическими союзами.
1 шаг. Нужно определить, сколько в данном сложном суждении простых суждений и провести границы между ними. Границы между суждениями часто подсказывают запятые.
2 шаг. Определяем логические союзы на границах между простыми суждениями.
3 шаг. Вместо границ поставить логические союзы, подходящие по смыслу и записать полученное суждение.
4 шаг. Обозначить простые суждения буквами, а союзы соответствующими символами и записать полученный результат. В нужных случаях целесообразно поставить скобки.
Образец:
Исходное суждение: «Любовь юная, прелестная, поэтическая, уносящая в мир грез, – на земле только она одна может дать счастье».
1 шаг. Определяем количество простых суждений в данном сложном суждении. Судя по запятым их четыре.
2 шаг. Между первыми тремя суждениями нужно поставить союз «и», а между этими тремя суждениями и четвертым возможен союз «и», а также союз «если, то».
3 шаг. Записываем, что получилось: «Если любовь есть юная и любовь есть прелестная и любовь есть поэтическая, то на земле только она одна может дать счастье».
4 шаг. Обозначаем простые суждения буквами, а союзы символами, и записываем то, что получилось: (a Λ b Λ c) →d
Виды сложных суждений:
а) конъюнкция: простые суждения связаны союзом «и». Обозначается значком Λ. Логический союз «и» выражается в тексте с помощью следующих слов: а, но, да, несмотря на, а также, хотя и, однако. Используются также знаки – (, : ; - .).
б) дизъюнкция: простые суждения связаны союзом «или». Есть два вида дизъюнкции. Слабая, где союз или означает: «или то, или другое, или то и другое вместе». Обозначается значком V. Сильная или строгая дизъюнкция, в которой союз «или» означает «либо одно, либо другое». Обозначается тем же значком V, только с точкой сверху.
в) импликация: простые суждения связаны союзом «если, то». Обозначается значком →.
г) эквиваленция: простые суждения связаны союзом «если и только если», «тогда и только тогда, когда». Обозначается значком: ↔
д) отрицание: к простому суждению присоединяется его отрицание «неверно, что», или «неправда, что», или «не». Обозначается знаком или черточкой над суждением.
5 ОПРЕДЕЛЕНИЕ ИСТИННОСТИ СЛОЖНОГО СУЖДЕНИЯ
Определить истинность сложного суждения можно в том случае, если известна истинность или ложность составляющих его простых суждений.
1 шаг. Выражаем сложное суждение в символической форме.
2 шаг. Исходя из того, что дано, приписываем каждому простому суждению истинность или ложность (можно подставляя сверху буквы «и» или «л».
3 шаг. По таблицам истинности определяем по порядку истинность или ложность составных частей сложного суждения, начиная с двух рядом находящихся суждений, связанных каким-либо логическим союзом. Если есть скобки, то начинать надо с того, что внутри скобок.
4 шаг. Записываем общий Ответ: «суждение истинно» или «суждение ложно».
Образец:
Исходное суждение: «Если человек начинает интересоваться смыслом жизни или ее ценностью – это значит, что человек болен».
1 шаг. Выражаем суждение в символической форме: (aΛb) → c.
2 шаг. Пусть а и b у нас будут истинными, а с будет ложным. а(и), b(и), с(л)
3 шаг. В скобках у нас конъюнкция. По таблице истинности конъюнкции определяем, что aΛb – иΛи = и (истинно). Далее определяем истинность импликации по таблицам истинности импликации: и→л= л.
4 шаг. Пишем общий ответ: Суждение ложно.
ТАБЛИЦЫ ИСТИННОСТИ:
а) Конъюнкция б) Слабая дизъюнкция в) Сильная дизъюнкция:
| А | В | A v В |
| и | и | и |
| и | л | и |
| л | и | и |
| л | л | л |
| А | В | A V B |
| и | и | л |
| и | л | и |
| л | и | и |
| л | л | л |
| А | В | А & В |
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | л |
| А | В | А ↔ В |
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | и |
| А | ~ А |
| и | л |
| л | и |
г) Импликация д)Отрицание е) Эквиваленция:
| А | В | A → В |
| и | и | и |
| и | л | л |
| л | и | и |
| л | л | и |
6 ОПРЕДЕЛЕНИЕ РАСПРЕДЕЛЕННОСТИ ТЕРМИНОВ СУЖДЕНИЯ
1 шаг. Представляем суждение в явной форме с квантором и логической связкой.
2 шаг. Определяем субъект и предикат суждения.
3 шаг. Определяем вид суждения.
4 шаг. По таблице определяем, распределены субъект и предикат или нераспределены.
5 шаг. Записываем ответ.
Образец:
Дано: «Бумага все стерпит».
1 шаг. Переводим в форму явного суждения: «Всякая бумага есть все терпящая».
2 шаг. Определяем субъект и предикат. Субъект здесь – «бумага», предикат – «все терпящая».
3 шаг. Определяем вид суждения. В данном случае – это общеутвердительное суждение.
4 шаг. Смотрим таблицу распределенности терминов. Определяем, что в общеутвердительном суждении субъект распределен, предикат нераспределен.
5 шаг. Записываем ответ: Субъект(бумага) – распределен, предикат(все терпящая) – нераспределен.
| ВИД суждения | символ | Субъект | Предикат |
| о-у | А | распределено | нераспределено |
| о-о | Е | распределено | распределено |
| ч-у | I | нераспределено | нераспределено |
| ч-о | О | нераспределено | распределено |
УМОЗАКЛЮЧЕНИЕ
1. НЕПОСРЕДСТВЕННОЕ УМОЗАКЛЮЧЕНИЕ
В непосредственных умозаключениях заключение делается из одной посылки. Противоречия между посылкой и заключением не должно быть!
Как сделать непосредственное умозаключение?
1 шаг. Представить высказывание в виде явного суждения, определить его вид, выразить в в символической форме его строение.
2 шаг. Выписать отдельно субъект(S) и отдельно предикат(Р). Разбивать субъект или предикат на части нельзя!
3 шаг. Найти формулу для данного вида суждения.
4 шаг. По формуле вывести из посылки заключение.
Образец:
Посылка: Студенты – люди веселые.
1 шаг. Студенты – люди веселые → Все студенты есть люди веселые, общеутвердительное - Все S есть Р.
2 шаг. Выписываем: S – студенты, Р – веселые.
3 шаг. Ищем формулу:
Список формул:
ОБРАЩЕНИЕ: субъект и предикат меняются местами – S - Р → Р - S.
Общеутвердительное(А): Все S есть Р → некоторые Р есть S.
Общеотрицательное(Е): Ни одно S → ни одно Р не есть S.
Частноутвердительное(I): Некоторые S есть Р → Некоторые Р есть S.
Частноотрицательное(О) : не обращается.
ПРЕВРАЩЕНИЕ: субъект тот же, предикат меняется на противоречащий - S - Р → S – не-Р.
Общеутвердительное(А): Все S есть Р → ни одно S не есть не-Р.
Общеотрицательное(Е): Ни одно S не есть не-Р → Все S есть не-Р.
Частноутвердительное(I): Некоторые S есть Р →некоторые S не есть не-Р.
Частноотрицательное(О): Некоторые S не есть Р → некоторые S есть не-Р.
ПРОТИВОПОСТАВЛЕНИЕ ПРЕДИКАТУ: Субъектом становится понятие, противоречащее предикату исходного суждения, а предикатом – субъект исходного суждения. S - Р → не-Р – S.
Общеутвердительное(А): Все S есть Р → ни одно не-Р не есть S.
Общеотрицательное(Е): Ни одно S не есть не-Р → некоторые не-Р есть S.
Частноутвердительное(I): не преобразуется.
Частноотрицательное(О): Некоторые S не есть Р → некоторые не-Р есть S.
Поскольку в нашем случае суждение общеутвердительное, то находим соответствующие формулы.
4 шаг. Выводим заключение.
Обращение: Все студенты есть люди веселые → Некоторые веселые люди есть студенты.
Превращение: Все студенты есть люди веселые → Ни один студент не есть невеселый.
Противопоставление предикату: Все студенты есть люди веселые → Ни один невеселый человек не есть студент.
2. АНАЛИЗ ПРОСТОГО КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА (ПКС)
В простом категорическом силлогизме две посылки и заключение.
1 шаг. Нужно сделать из двух посылок заключение
2 шаг. Определяем меньший, больший, средний термины силлогизма.
Субъект заключения (S) – меньший термин.
Предикат заключения (Р) – больший термин.
Средний термин(М) повторяется в обеих посылках.
3 шаг. Рисуем схему силлогизма. Заключение всегда: S - Р
4 шаг. Определяем фигуру силлогизма. Всего существует 4 фигуры ПКС.
5 шаг. Определяем модус силлогизма.
Образец:
Все кошки есть себе на уме.
Мурка есть кошка.
?
1 шаг. Делаем заключение: Мурка есть себе на уме.
2 шаг. Определяем термины силлогизма.
Субъект заключения (S) – меньший термин - Мурка
Предикат заключения (Р) – больший термин. – себе на уме.
Средний термин (М) – кошка.
3 шаг. Рисуем схему ПКС.
М – Р
S - М
S – Р
4 шаг. Определяем фигуру силлогизма:
Всего существует 4 фигуры ПКС.
Первая фигура:
М – Р
S - М
S – Р
Вторая фигура:
Р – М
S - М
S – Р
Третья фигура
М – Р
М - S
S – Р
Четвертая фигура
Р – М
М - S
S – Р
Наш силлогизм соответствует первой фигуре ПКС. Так и запишем: первая фигура ПКС.
5 шаг. Определяем модус фигуры. Модус символизируется тремя буквами, которые обозначают виды суждения в посылках и заключении.
У нас первая посылка «Все кошки есть себе на уме» есть суждение общеутвердительное, значит, - а.
Вторая посылка «Мурка есть кошка» есть суждение единичное утвердительное, а оно считается за общее утвердительное, значит, опять – а.
И заключение «Мурка есть себе на уме» есть суждение единичное утвердительное, а оно считается за общее утвердительное, значит, – а.
В итоге получаем: модус силлогизма – ааа.
3. ПОИСК ОШИБОК В ПКС И ИХ ИСПРАВЛЕНИЕ
1 шаг. Определяем фигуру и модус силлогизма.
2 шаг. Смотрим, соответствует ли наш силлогизм правильным модусам фигуры.
3 шаг. Если не соответствует, то проверяем ПКС на ошибки. Сначала проверяем, нет ли нарушения общих правил ПКС, затем проверяем нарушение правил данной фигуры ПКС.
4 шаг. Если нарушения есть, то указываем письменно их по формуле: «нарушено правило ПКС, гласящее то-то» и «нарушено правило такой-то фигуры силлогизма, гласящее то-то».
5 шаг. Исправляем заключение по правильному модусу. Если сделать вывод невозможно (посылки менять нельзя), то пишем: «вывод невозможен».
Образец:
Все собаки кусаются.
Все кошки кусаются.
Некоторые собаки есть кошки.
1 шаг. Определяем фигуру – фигура вторая. Определяем модус – ааi.
2 шаг. Смотрим, соответствует ли наш модус правильным модусам второй фигуры.
Модусы первой фигуры: ааа, еае, аii, еiо.
Модусы второй фигуры: еае, аее, еiо, аоо.
Модусы третьей фигуры: ааi, iai, aii, eao, oao, eio.
Модусы четвертой фигуры: aai, aee, iai, eao, eio.
Модуса нашего силлогизма в списке правильных модусов второй фигуры нет. Значит, есть ошибка.
3 шаг. Ищем, какое правило ПКС и правило второй фигуры нарушено.
4 шаг. Пишем, какие правила нарушены. Видно, что нарушено правило ПКС, гласящее, что средний термин должен быть распределен хотя бы в одной из посылок. Нарушено также правило второй фигуры ПКС, гласящее, что одна из посылок и заключение должны быть отрицательными суждениями. Ошибка: «Две утвердительные посылки».
5 шаг. Исправить данный силлогизм невозможно, так как нужна отрицательная посылка. Поэтому пишем: «вывод невозможен».
4. ВОССТАНОВЛЕНИЕ ЭНТИМЕМЫ В ПОЛНЫЙ СИЛЛОГИЗМ
Энтимема – это сокращенный силлогизм, в котором пропущена одна из посылок или заключение.
Восстановление энтимемы в полный силлогизм:
1 шаг. Если пропущено заключение, то нужно его сделать. Если пропущена посылка, то нужно установить, что является заключением.
2 шаг. Определяем меньший, больший, средний термины силлогизма. В заключении всегда – меньший и больший термины.
3 шаг. Представляем силлогизм в виде схемы. Обозначаем заключение и имеющуюся посылку символами.
4 шаг. Определяем, какие термины должны быть в недостающей посылке. Можно подобрать подходящий модус данной фигуры и по нему восстановить недостающую посылку.
5 шаг. Записать: недостающая посылка: «то-то, то-то».
6. шаг. Сформулировать силлогизм в полном виде. Проверить правильность силлогизма. Определить его фигуру и модус.
Образец.
Ж. Алферов - академик, поэтому Ж. Алферов – умный.
1 шаг. Устанавливаем заключение. Это суждение «Ж. Алферов – умный».
2 шаг. Определяем термины силлогизма. Меньший – Ж. Алферов, больший – умный, средний – академик.
3 шаг. Обозначаем термины символами и рисуем схему силлогизма:
------
S - М
S – Р
4 шаг. В имеющейся посылке есть средний и меньший термины. В недостающей посылке должны присутствовать средний и больший термины, то есть: академик и умный.
5 шаг. Формулируем. Недостающая посылка: «Все академики – умные».
6 шаг. В итоге получаем:
Все академики – умные.
Ж. Алферов – академик.
Ж. Алферов – умный.
Первая фигура, модус ааа. Силлогизм правильный, ошибок нет.
Дата добавления: 2015-04-15; просмотров: 167; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Будь готов быстро меняться, снова и снова наслаждаясь этим | | | СОПУТСТВУЮЩИЕ СИМПТОМЫ |