Суммарный коэффициент рождаемости. Теперь вернемся снова к возрастным коэффициентам рождаемости

Теперь вернемся снова к возрастным коэффициентам рождаемости. Если иметь в виду упомянутые трудности с использованием коэффициен­тов брачной рождаемости, то обычные, не дифференцированные по брач­ному состоянию возрастные коэффициенты остаются наилучшими показа­телями уровня рождаемости, дающими хорошие возможности для анализа его состояния и динамики. Как уже отмечалось, их достоинством является независимость от влияния возрастной структуры внутри женского репродуктивного возрастного контингента. Но и у них есть недостаток, который состоит в том, что их много. При использовании однолетних коэффициен­тов их будет целых 35 (от 15 до 49 лет включительно).

В случае использования пятилетних коэффициентов их число уже значи­тельно меньше — 7, но все же их остается еще много для обозрения. Причем динамика коэффициентов может быть различной, иногда до противополож­ности. В самом деле, тенденция динамики коэффициентов в большинстве экономически развитых стран в нынешнем веке была такой, что в младших возрастных группах коэффициенты рождаемости росли,в то время как в старших — снижались. Иногда, глядя на картину динамики возрастных ко­эффициентов рождаемости, трудно решить, что же все-таки происходит — снижается рождаемость или растет. И некоторые научные спекулянты небес­корыстно пользуются этим обстоятельством, утверждая, будто рождаемость в нашей стране не снижается. Нужен один обобщающий показатель, который соединял бы в себе достоинства целой системы показателей. И такой показа­тель есть. Его зовут — суммарный коэффициент рождаемости.

Суммарный коэффициент рождаемости вычисляется путем суммирования возрастных коэффициентов рождаемости с умножением их на длину каждого возрастного интервала в целых годах (при однолетних коэффици­ентах множитель равен 1, при пятилетних — 5, и т. д.). Сумма в итоге де­литсяна 1000, т.е. показатель выражается в расчете на одну женщину в среднем. Формула расчета такова:

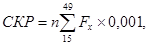(5.6.1)

где СКР — суммарный коэффициент рождаемости; F_x — возрастные коэффициенты; n — длина возрастного интервала (при одинаковой длине ин­тервала, его можно вынести за знак суммы, т.е. сначала сложить коэффициенты, а затем один раз умножить сумму коэффициентов на длину возрастного интервала. Если же интервалы разные по длине (редко, но бывает), то придется каждый коэффициент умножать отдельно на соответствующую ему длину возрастного интервала).

Суммарный коэффициент рождаемости является одним из сводных, итоговых показателей, которые строятся как по методу реального, так и условного поколения. Приведенная выше формула расчета суммарного коэффициента относится к условному поколению, т.е., мы рассматриваем все возрастные коэффициенты рождаемости, относящиеся к разным реальным поколениям женщин, условно как относящиеся к одному поколению, будто бы прожившему в данном одном календарном году, в году наблюде­ния, всю свою репродуктивную жизнь, с 15 до 50 лет.

Суммарный коэффициент рождаемости показывает, сколько де­тей рожает в среднем одна женщина за всю свою жизнь с 15 до 50 лет при условии, что на всем протяжении репродуктивного периода жиз­ни данного поколения возрастные коэффициенты рождаемости в каждой возрастной группе остаются неизменными на уровне расчетного периода[67].

Рассмотрим пример расчета суммарного коэффициента рождаемости (см. таблицу 5.1).

Таблица 5.1