
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
СССР и снова в России
Снижение рождаемости в нашей стране началось давно (вопреки спекуляциям на этой проблеме некоторых нынешних политиков и ученых, утверждающих, будто рождаемость в России упала лишь несколько лет назад в результате экономических реформ), более 100 лет назад. Долгое время на эту тенденцию никто не обращал внимания. Как уже говорилось ранее, параллельно со снижением рождаемости быстро снижалась детская смертность и число детей в семьях в среднем долгое время оставалось прежним или близким к тому. Одним из первых на эту тенденцию обратил внимание в 1914 г. классик нашей демографии, академик медицины Сергей Александрович Новосельский (1872—1953). В статье, посвященной этому вопросу[75] он отметил «прогрессирующее распространение среди населения неомальтузианской практики»[76] (так в то время именовали практику абортов и контрацепции), причем не только среди городского, но среди сельского населения. В той же статье С.А. Новосельский предсказывал также, что «если понижение рождаемости в своем темпе станет быстро обгонять понижение смертности, то и у нас политическим деятелям придется считаться со злободневным для Западной Европы вопросом о возможности противодействия прогрессирующему падению рождаемости»[77].
К сожалению, это предостережение не получило никакого резонанса в нашей науке, ни во время публикации статьи, ни впоследствии. Не имела эта мысль продолжения и в последующем творчестве самого С.А. Новосельского, хотя статья переиздавалась дважды в сборниках его избранных произведений в 1958 и 1978 гг. (правда, в урезанном издателями виде).
С конца 1960-х гг., казалось, наметилась переломная тенденция: общие коэффициенты рождаемости начали повышаться. За период с 1968—1969 гг.[78] и по 1979—1980 гг. они поднялись с 14,2 до 15,9 ‰, или на 12,0%. Причем, на всем протяжении почти 12-летнего периода подъем происходил почти без колебаний (см. таблицу 5.5). Многие ученые писали тогда о якобы наметившемся переломе в тенденциях рождаемости, о том, что рождаемость и далее будет расти, свидетельствуя об успехах руководства страны в создании благосостояния для народа (в то время уровень рождаемости служил одним из показателей благосостояния. Поэтому показатели рождаемости были не только демографическими, но и политическими индикаторами). Однако, если использовать суммарные коэффициенты рождаемости (которые в те времена еще не вошли в практику), то динамика уровня рождаемости оказывается иной. После небольшого и незначительного подъема суммарного коэффициента в 1968—1972 гг., он неуклонно снижался,с 2,053 в 1971—1972 гг. до 1,888 в 1979—1980 гг., или на 8,0%.
Рассмотрим динамику общего коэффициента рождаемости за последние 35 лет с помощью индексного метода, который позволит нам выявить роль каждого из факторов, обусловивших изменение уровня рождаемости. Для расчетов нам понадобится формула общего коэффициента рождаемости в таком виде, который отражает его соотношение с возрастными коэффициентами рождаемости и возрастной структурой населения. Это соотношение можно представить в виде следующей формулы:
 (5.1.2)
(5.1.2)
где, напомню, условные обозначения следующие: п — общий коэффициент рождаемости; N — число родившихся; 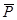 — среднегодовая численность населения;
— среднегодовая численность населения;  — численность женщин в возрасте от 15 до 50 лет; F — специальный коэффициент рождаемости; и — доля женщин в возрасте 15—49 лет в общей численности населения (в долях единицы). Добавим к этому выражение специального коэффициента рождаемости в виде средней из возрастных коэффициентов рождаемости, взвешенных по долям женщин каждой соответствующей возрастной группы женщин в составе женского возрастного репродуктивного контингента (15 — 49 лет). В виде формулы это будет выглядеть так:
— численность женщин в возрасте от 15 до 50 лет; F — специальный коэффициент рождаемости; и — доля женщин в возрасте 15—49 лет в общей численности населения (в долях единицы). Добавим к этому выражение специального коэффициента рождаемости в виде средней из возрастных коэффициентов рождаемости, взвешенных по долям женщин каждой соответствующей возрастной группы женщин в составе женского возрастного репродуктивного контингента (15 — 49 лет). В виде формулы это будет выглядеть так:
 (5.11.1)
(5.11.1)
где Fx — возрастные коэффициенты рождаемости; wx = доля женщин возрастной группы «х» в численности женщин 15—49 лет.
Теперь, чтобы измерить изменения коэффициента п за период времени, обозначим коэффициент в начале периода нижним индексом 0, в конце периода — 1. Изменение коэффициента за период времени от 0 до 1 будет следующим:
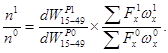 (5.11.2)
(5.11.2)
Введем в числитель и знаменатель правой крайней дроби одно и то же число — (отчего, естественно, величина всего выражения не изменится) и произведем простую перестановку элементов, отчего все выражение примет окончательный вид системы индексов:
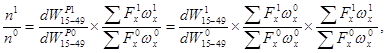 (5.11.3)
(5.11.3)
где левая часть равенства выражает относительное изменение величины общего коэффициента рождаемости, а правая — три фактора (индекса) этого изменения. Первая дробь (частное — индекс) в правой части уравнения (соотношение dW15-49) показывает изменение общего коэффициента за счет изменения доли женщин 15—49 лет в населении; второй индекс (индекс постоянного состава) характеризует изменение того же общего коэффициента рождаемости за счёт изменения возрастных коэффициентов рождаемости, т.е. собственно рождаемости (числитель и знаменатель этого индекса различаются коэффициентами рождаемости, в то время как возрастная структура женского репродуктивного контингента постоянна); наконец, третий индекс, напротив, выражает изменение общего коэффициента рождаемости за счет изменения только возрастной структуры женщин (индекс переменного состава). Приведенная выше формула расчетов может кого-то и отпугнуть своей внешней громоздкостью. Однако хочу обратить внимание читателя на то, что считать надо всего лишь один элемент (одну колонку) этой формулы —  Остальные элементы выписываются из демографического ежегодника. Ниже приводится пример расчета индексов изменения общего коэффициента рождаемости в России за период 1990—1995 гг. (таблица 5.5).
Остальные элементы выписываются из демографического ежегодника. Ниже приводится пример расчета индексов изменения общего коэффициента рождаемости в России за период 1990—1995 гг. (таблица 5.5).
Из демографического ежегодника выписываем необходимые для расчета данные: общие коэффициенты рождаемости за 1990 и 1995 гг. равны соответственно 13,4 и 9,3‰; специальные коэффициенты — 55,3 и 36,0‰; долю женщин 15—49 лет в общей численности населения получаем расчетом из соотношения общего и специального коэффициентов, которые нам известны. В результате получим соответственно 24,2 и 25,8%.
Теперь осталось только подставить все необходимые данные в формулу, и получим:

Таблица 5.5
Дата добавления: 2015-04-16; просмотров: 244; Мы поможем в написании вашей работы!; Нарушение авторских прав |