
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет цепи методом наложения
Изобразим основную (рис. 2.4, а) и дополнительные схемы (см.рис. 2.4, б, в), в последних оставляем по одной эдс , а вторую эдс закорачиваем. На рис. 2.4, б, в обозначим положительные направления токов в ветвях.

Рис. 2.4. Расчетные схемы: а)-основная; б) и в) -дополнительные - для определения частичных токов
Рассчитаем частичные токи. Для схемы рис. 2.4, б:



По первому закону Кирхгофа для узла в
I′3 = I′1 - I′4 = 15,488 - 13,536 - 1,952 A .
Токи I2 и I5 обратно пропорциональны сопротивлениям этих ветвей и определяются так:
I′2 =I′3 ∙  = 1,952
= 1,952 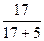 = 1,508 A;
= 1,508 A;
I′5 = I′3 ∙  = 1,952
= 1,952  = 0,444 A.
= 0,444 A.
Для схемы рис. 2.4, в


Переносим частичные токи схем рис. 2.4, б, в на основную расчетную схему рис. 2.4, а и по их направлению и значению определяем действительные токи основной схемы.
II = I′I + I″I = 15,488 + 1,257 = 16,745 A;
I2 = I′2 + I″2 = 1,508 + 8,432 = 9,940 A;
I3= I′3 + I″3 = 1,952 + 5,030 = 6,982 A;
I4 = I′4 - I″4 = 13,536 - 3,773 = 9,763 A;
I5 = I″5 - I′5 = 3,402 -0,444 = 2,958 A.
Токи I4 и I5 находим вычитанием соответствующего меньшего тока от большего и направляем в сторону большего частичного тока. Примечание: При расчете частичных токов для расчетных цепей 3, 5, 8, 9, 11, 16, 17, 18, 19, 20, 26, 28, 29 нужно применять преобразования схемы "треугольник" сопротивлений в эквивалентную "звезду" сопротивлений по формулам
 ;
;  ;
;  ;
;
где R1, R2 , R3 - сопротивления "треугольника";
R12 , R23, R13 - эквивалентные значения "звезды" сопротивлений.
Дата добавления: 2015-04-16; просмотров: 223; Мы поможем в написании вашей работы!; Нарушение авторских прав |