ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Рассматривая переходные процессы в конкретных цепях, нужно руководствоваться законами коммутации, согласно которым ток в цепи, обладающей индуктивностью, и напряжение на конденсаторе не могут изменяться скачком.

В учебнике даны обоснования этим законам.

Если реальную катушку, обладающую индуктивностью L и сопротивлением R, включить под постоянное напряжение U (рис. 25), замкнув выклю­чатель В₁, то при появлении тока в катушке будет наводиться ЭДС самоиндукции:

Она войдет в уравнение, составленное по второму закону Кирхгофа:

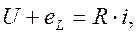или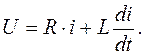

Рисунок 25

Решив полученное дифференциальное уравнение, можно выявить закон изменения тока. В учебниках оно решено разными методами, но результат одинаков:

где е = 2,72 – основание натуральных логарифмов;

t – текущее время;

τ= L/R, измеряется в секундах и называется постоянной времени.

Исследуя полученное выражение, можно установить, что появившийся ток будет постепенно увеличиваться и по истечении бесконечно длительного времени приобретет установившееся значение.

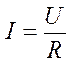
Умножив левую и правую части дифференциального уравнения на (i·dt), получим баланс энергии:

.

Левая часть выражает энергию, полученную от источника, первое слагаемое – энергию, рассеянную в виде тепла, второе слагаемое – энергию, запасенную в магнитном поле катушки. При изменении тока от нуля до какого-либо значения I запас энергии в магнитном поле составит:

Если катушку, соединенную с источником энергии, замкнуть выключателем В₂, то ток в катушке будет поддерживать ЭДС самоиндукции:

,

откуда ,

где I – ток в момент замыкания катушки.

Последнее выражение показывает, что ток снизится до нуля за беско­нечно длительное время. За это же время выделится в виде тепла вся ра­нее запасенная энергия W_M.

Аналогичные процессы происходят в цепи с последовательно соеди­ненными конденсатором и резистором (рис. 26).

Рисунок 26

После включения такой цепи под постоянное напряжение на электродах конденсатора начинают накапли­ваться одинаковой величины с противоположными знаками заряды:

где С – емкость конденсатора.

Мгновенное значение зарядного тока выражается производной:

В соответствии со вторым законом Кирхгофа:

Решив это дифференциальное уравнение, можно получить законы изменения напряжения на конденсаторе и зарядного тока:

.

Постоянная времени τ зависит от параметров R и С:

.

Из баланса энергии следует:

.

Количество энергии, запасаемой в электрическом поле конденсатора при увеличении напряжения от нуля до какого-либо значения U,составит:

.

Если конденсатор переключателем К отключить от источника энергии и замкнуть на резистор, то конденсатор начнет разряжаться. Запасенная энергия будет выде­ляться в резисторе в виде тепла. Мгновенное значение тока можно выразить по закону Ома, а также производной заряда по времени:

и

Следовательно:

.

После решения этого уравнения определяются законы изменения напряжения на конденсаторе и тока:

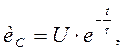
Здесь U – напряжение в начале разрядки.

Графики изменения напряжений и токов при переходных процессах представлены в учебнике. Все рассмотренные процессы теоретически протекают бесконечно долго. Практически любой из них можно считать законченным по истечении времени в 4 или 5 значений τ. Если взять t = 4,6 τ, то e^-4,6≈0,01.

Следовательно, напряжение или ток будут отличаться от установившегося значения всего на 1 %.

В учебнике можно найти примеры практического применения явлений, возникающих при переходных процессах, а также примеры возможных нежелательных последствий.