Туннельный эффект

Факультет физико-математических и компьютерных наук

Кафедра электроники телекоммуникаций и компьютерных технологий

КУРСОВАЯ РАБОТА

по дисциплине «Физические основы электроники и электротехники»

на тему:

«Эффект туннелирования в электронике»

Выполнил:

Студент группы ИС-2

Черных Ярослав Владиславович

(подпись)___________________

Проверил:

к.п.н., доцент

Мицук Сергей Васильевич

Липецк 2014

Содержание

1. Туннельный эффект. 3

2.1. КОНТАКТ МЕТАЛЛ-МЕТАЛЛ.. 6

2.2. СТРУКТУРА МЕТАЛЛ-ДИЭЛЕКТРИК-МЕТАЛЛ.. 10

2.3. ТОКОПЕРЕНОС В ТОНКИХ ПЛЁНКАХ.. 13

2.4. ТУННЕЛЬНЫЙ ПРОБОЙ В p-n-ПЕРЕХОДЕ.. 16

2.5. ЭФФЕКТЫ ДЖОЗЕФСОНА.. 18

2.6. ЭФФЕКТ ФРАНЦА-КЕЛДЫША.. 21

3. ТУННЕЛЬНЫЙ ДИОД.. 23

ЛИТЕРАТУРА.. 29

Туннельный эффект

Рассмотрим поведение частицы при прохождении через потенциальный барьер. Пусть частица, движущаяся слева направо, встречает на своём пути потенциальный барьер высоты U₀ и ширины l (рис. 1.1). По классическим представлениям движение частицы будет таким:

- если энергия частицы будет больше высоты барьера (E>U₀), то частица беспрепятственно проходит над барьером;

- если же энергия частицы будет меньше высоты барьера (E<U₀), то частица отражается и летит в обратную сторону; сквозь барьер частица проникнуть не может.

Совершенно иначе поведение частицы по законам квантовой механики. Во-первых, даже при E>U₀ имеется отличная от нуля вероятность того, что частица отразится от потенциального барьера и полетит обратно. Во-вторых, при E<U₀ имеется вероятность того, что частица проникнет «сквозь» барьер и окажется в области III. Такое поведение частицы описывается уравнением Шрёдингера:

. (1.1)

Здесь - волновая функция микрочастицы. Уравнение Шрёдингера для области I и III будет одинаковым. Поэтому ограничимся рассмотрением областей I и II. Итак, уравнение Шрёдингера для области I примет вид:

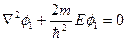, (1.2)

введя обозначение:

, (1.4)

окончательно получим:

(1.5).

Аналогично для области II:

, (1.6)

где . Таким образом, мы получили характеристические уравнения, общие решения которых имеют вид:

при x<0, (1.7)

при x>0 (1.8)

Слагаемое соответствует волне, распространяющейся в области I в направлении оси х, А₁- амплитуда этой волны. Слагаемое 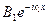соответствует волне, распространяющейся в области I в направлении, противоположном х. Это волна, отражённая от барьера, В₁- амплитуда этой волны. Так как вероятность нахождения микрочастицы в том или ином месте пространства пропорциональна квадрату амплитуды волны де Бройля, то отношение представляет собой коэффициент отражения микрочастицы от барьера.

Слагаемое соответствует волне, распространяющейся в области II в направлении х. Квадрат амплитуды этой волны отражает вероятность проникновения микрочастицы в область II. Отношение представляет собой коэффициент прозрачности барьера.

Слагаемое должно соответствовать отражённой волне, распространяющейся в области II. Так как такой волны нет, то В₂ следует положить равным нулю.

Для барьера, высота которого U>E, волновой вектор k₂ является мнимым. Положим его равным ik, где 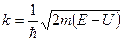является действительным числом. Тогда волновые функции и приобретут следующий вид:

(1.9)

(1.10)

Так как , то это значит, что имеется вероятность проникновения микрочастицы на некоторую глубину во вторую область. Эта вероятность пропорциональна квадрату модуля волновой функции :

. (1.11)

Наличие этой вероятности делает возможным прохождение микрочастиц сквозь потенциальный барьер конечной толщины l (рис. 1.1). Такое просачивание получило название туннельного эффекта. По формуле (1.11) коэффициент прозрачности такого барьера будет равен:

, (1.12)

где D₀ – коэффициент пропорциональности, зависящий от формы барьера. Особенностью туннельного эффекта является то, что при туннельном просачивании сквозь потенциальный барьер энергия микрочастиц не меняется: они покидают барьер с той же энергией, с какой в него входят.

Туннельный эффект играет большую роль в электронных приборах. Он обуславливает протекание таких явлений, как эмиссия электронов под действием сильного поля, прохождение тока через диэлектрические плёнки, пробой p-n перехода; на его основе созданы туннельные диоды, разрабатываются активные плёночные элементы.

2.

Дата добавления: 2015-04-16; просмотров: 10; Нарушение авторских прав