Замена треугольника сопротивлений эквивалентной звездой

Проведем преобразование «треугольника» bcd, соответствующего схеме электрической цепи, в эквивалентную «звезду» (рис. 2). Исходный треугольник образован сопротивлениями R₄, R₅, R₆. При преобразовании обязательно сохраняется условие эквивалентности схем, т.е. токи в проводах, проходящих к преобразуемой схеме, и напряжения между узлами не меняют своих величин.

При преобразовании «треугольника» в «звезду» используем расчетные формулы:

Ом; (1.8)

Ом; (1.9)

Ом. (1.10)

В результате преобразования исходная схема упрощается (рис. 3).

В преобразованной схеме только три ветви и соответственно три тока I₁, I₂, I₃. Для расчета этих токов достаточно иметь систему трех уравнений, составленных по законам Кирхгофа:

(1.11)

При составлении уравнений направление тока и обхода контуров выбирается так же, как и в трехконтурной схеме.

Составляем и решаем систему:

(1.12)

Решив матрицу, получим неизвестные значения токов I₁, I₂, I₃:

I₁ = 1,297 А;

I₂ = –1,376 А;

I₃ = 0,079 А.

Подстановкой полученных значений токов в уравнения, составленные для трехконтурной схемы, определим остальные токи I₄, I₅, I₆:

I₄ = 0,23 А;

I₅ = 0,151 А;

I₆ = –1,146 А.

1.3 Расчет методом «Контурных токов»

Произвольно задаемся направлением контурных токов в ячейках исходной схемы. Удобнее все токи указать в одном направлении – по часовой стрелке (рис. 4).

Составляем для каждого контура-ячейки уравнение по второму закону Кирхгофа, обходя контур по часовой стрелке.

Уравнение для первого контура:

E₃ – E₁ = I₁₁ · (R₁ + R₀₁ + R₃ + R₀₃ + R₅) – I₃₃ · (R₃ + R₀₃) – I₂₂ · R₅; (1.13)

уравнение для второго контура:

0=I₂₂· (R₄+R₅+R₆) –I₁₁·R₅ –I₃₃· R₄; (1.14)

уравнение для третьего контура:

E₂–E₃=I₃₃·(R₂+R₀₂+R₃+R₀₃+R₄)–I₁₁·(R₃+R₀₃)–I₂₂·R₄. (1.15)

Решаем составленные уравнения совместно как систему:

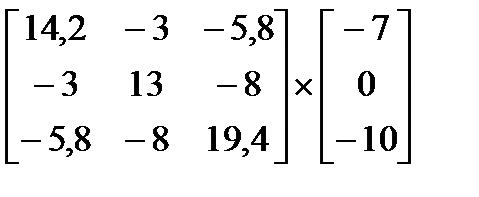=> (1.16)

Получаем значения контурных токов:

I₁₁ = –1,297 А;

I₂₂ = –1,146 А;

I₃₃ = –1,376 А.

Если контурный ток оказался отрицательным, значит, его направление противоположно выбранному на схеме.

Токи во внутренних ветвях схемы I₁, I₄, I₅ определяются как сумма или разность соответствующих контурных токов. Если контурные токи в ветви совпадают по направлению, берется их сумма; если не совпадают, берется их разность:

I₃ = I₁₁ – I₃₃= –1,297–(–1,376) =0,076 А; (1.17)

I₄ = I₂₂ – I₃₃ = –1,146 – (–1,376) = 0, 23 А; (1.18)

I₅ = I₂₂ – I₁₁ = –1,146 – (– 1,297) = 0,151 А. (1.19)

Токи во внешних ветвях схемы I₂, I₃, I₆ равны соответствующим контурным токам:

I₁ = –I₁₁ = 1,297 А;

I₂ = I₃₃ = –1,376 А;

I₆ = I₂₂ = –1,146 А.