Методические указания по выполнению курсовой работы

Анализ режимов работы трехфазной цепи

Для расчета трехфазных цепей, работающих в установившемся режиме необходимо знать основные соотношения между токами и напряжениями каждой фазы, линейными и фазными напряжениями и токами, способы эквивалентной замены соединения “звезда” соединением “треугольник” и наоборот. Все соотношения, равно как и способы эквивалентной замены соединения “звезда” соединением “треугольник” и наоборот приведены в учебниках и рассматриваются в лекционных курсах, однако студенты не всегда имеют достаточные навыки использования учебников и материала теоретических курсов, поэтому целью настоящих методических указаний является оказание помощи студентам в правильном выборе соответствующих разделов теоретического курса с последующим использованием основных теоретических соотношений в осуществлении практических расчетов цепей близких к реальным по своей структуре.

1. Расчет трехфазной сети без компенсатора реактивной мощности второго приемника.

В соответствии с заданием известными являются: суммарная активная мощность второго приемника Р₂, коэффициент мощности этого приемника cos j₂, активные мощности фаз первого приемника P_A, P_B, P_C и действующее значение линейного напряжения.

Для вычисления линейных и фазных токов приемников и источника, прежде всего, необходимо правильно записать законы изменения мгновенных значений линейных и фазных напряжений в функции времени. Необходимо помнить о том, что при равенстве между собой амплитуд линейных напряжений и равенстве между собой амплитуд фазных напряжений их начальные фазы отличаются на 120 градусов. Для дальнейшего выполнения вычислений необходимо записать комплексные действующие значения соответствующих величин.

Второй приемник представляет собой для источника симметричную нагрузку, поэтому действующие значения фазных токов могут быть найдены по известным полным мощностям каждой фазы, которые равны трети полной мощности второго приемника:

Для соединения “звезда”:

S_2A=S_2B=S_2C=1/3 S₂, S₂=Р₂/cos j₂, Q₂=S₂×sinj₂.

Для соединения “треугольник”:

S_2AB=S_2BC=S_2CA=1/3 S₂.

Действующие значения фазных токов вычисляются по известным мощностям фаз и фазным напряжениям:

Для соединения “звезда” ток фазы А, например:

I_A=S_A/U_A.

Для соединения “треугольник”:

I_2AB=S_AB/U_AB.

Линейные токи приемника, соединенного “звездой” равны фазным токам. Линейные токи приемника, соединенного “треугольником” вычисляются по известным уравнениям, записанным на основании первого закона Кирхгофа в комплексной форме:

I_2A=I_2AB–I_2CA

I_2B=I_2BC–I_2AB

I_2C=I_2CA–I_2BC .

В случае симметричной нагрузки при соединении нагрузки “треугольником” действующие значения линейных токов в Ö3 раз больше фазных токов, например:

После вычисления действующих значений фазных и линейных токов необходимо записать их комплексные действующие значения для использования при построении векторных диаграмм.

Для вычисления фазных токов первого приемника, коэффициент мощности которого равен единице, необходимо использовать мощность соответствующих фаз.

Ток фазы А первого приемника, например, I_1A=P_1A/U_A. Фазное напряжение фазы А первого приемника определено ранее с учетом того, что фазные сопротивления нагрузки соединены “звездой” с нулевым проводом.

Линейные токи первого приемника равны фазным.

После вычисления фазных токов необходимо записать их комплексные действующие значения по известным комплексным действующим значениям соответствующих фазных напряжений.

Ток нулевого провода первого приемника вычисляется из уравнения:

I₀= I_1A+ I_1B+ I_1С.

После вычисления линейных токов первого и второго приемников можно вычислить токи источника, комплексные действующие значения которых равны сумме соответствующих токов приемников. Ток фазы А источника, например,

I_A= I_1A+ I_2A.

Коэффициент мощности трехфазной сети, состоящей из двух приемников, определится из формулы:

,

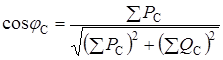где SP_C - сумма активных мощностей приемников, SPQ - сумма реактивных мощностей приемников.

Полная мощность сети:

,

или в комплексной форме:

S_C=SP_C+j SQ_C.

Производителей электрической энергии, как правило, в меньшей степени интересуют коэффициенты мощностей отдельных фаз.

2. Построение векторных диаграмм напряжений и токов источника и приемников.

Ранее рекомендовалось записывать напряжения и полученные в результате расчетов токи в комплексной форме. При наличии правильной записи токов и напряжений в комплексной форме построение векторной диаграммы не вызывает особых затруднений. Достаточно правильно выбрать масштабы длин векторов напряжений и токов. Каждый вектор проводится на векторной диаграмме под углом, равным начальной фазе, соответствующей синусоидальной величины. Не следует забывать о том, что начальная фаза равна аргументу соответствующего комплексного действующего значения.

Общий вид векторной диаграммы приведен на рисунке 2.

В том случае, когда заданием предусмотрено соединение нагрузки второго потребителя “треугольником”, рекомендуется сначала отдельно построить векторную диаграмму токов и напряжений

Рис. 2

второго приемника отдельно, а при построении векторной диаграммы всей сети учесть лишь линейные токи второго приемника.

При анализе векторной диаграммы сети следует обратить внимание на фазовые сдвиги между фазными напряжениями источника и соответствующими линейными токами. Кроме этого следует оценить величину тока нулевого провода I_o и его соотношение с фазными токами первого приемника и линейными токами источника.

3. Развернутая схема трехфазной сети с отключенным компенсатором.

Для представления развернутой схемы трехфазной сети необходимо, прежде всего, вычислить величины фазных сопротивлений приемников. Внутренние сопротивления источника заданы.

Сопротивления эквивалентных резисторов фаз первого приемника легко определяются мощностью фазной нагрузки и фазным напряжение. Сопротивление фазы В первого приемника, исходя из общей формулы для резистивной нагрузки P_A=U_A²/R_A, определится R_A=U_A²/R_A.P_A.

Полные сопротивления фаз второго приемника легко определить, если полная мощность второго приемника записана в комплексной форме: S₂= S₂e^jj2.

Тогда для сопротивления “звезда” Z_A=3U_A²/S₂^*.

В случае соединения “треугольник” Z_AB=3U_AB²/S₂^*.

Очевидно то, что фазные сопротивления второго приемника индуктивно-резистивного характера, поэтому из комплексной формы записи сопротивления определяются величины эквивалентных активного и реактивного сопротивлений. По значению последнего вычисляется индуктивность фазной нагрузки. Общий вид принципиальной схемы приведен на рис.3.

Рис.3

4. Расчет параметров компенсатора.

Для улучшения эффективности работы источника и устройств передачи электроэнергии к величине коэффициента мощности предъявляются жесткие требования. Ранее уже говорилось о том, что в реальных условиях работы предприятий cos j самого предприятия в целом, как правило, ниже допустимого значения. Для улучшения такого важного показателя как коэффициент мощности потребители используют устройства компенсации реактивной мощности. Эту роль могут выполнять электромашинные компенсаторы или устройства, базирующиеся на использовании батарей конденсаторов большой емкости. Сами компенсаторы могут иметь внутренние дополнительные потери мощности, но положительный результат от их использования подтверждается практикой.

В задании требуется подобрать параметры компенсатора таким образом, чтобы результирующий коэффициент мощности второго приемника при включенном компенсаторе не выходил бы за пределы допустимого значения, указанного в таблице вариантов. При этом необходимо учесть дополнительную мощность потерь компенсатора.

Активная мощность, рассеиваемая вторым потребителем:

P₂=S₂cos j₂.

Реактивная мощность второго потребителя:

Q₂=S₂sin j₂.

При подключенном компенсаторе суммарная активная мощность второго приемника составит:

P_2к=P_к+P₂.

Cуммарная реактивная же мощность

Q_2к=Q_к+Q₂.

Допустимое значение:

.

Из приведенной формулы достаточно легко можно получить значение Q_2к, при котором обеспечивается требуемое значение

cos j_2к. Таким образом:

Q_к=Q_2к– Q₂.

По заданной ранее мощности потерь компенсатора P_к и найденной реактивной мощности Q_к можно определить параметры эквивалентной схемы замещения компенсатора. Для упрощения дальнейших расчетов рекомендуется определить параметры последовательной схемы замещения фазных нагрузок, соединенных “звездой”.

Тогда S_к=P_к+jQк, и аналогично тому, как это уже выполнялось для определения параметров элементов схемы замещения второго приемника, соединенного “звездой”:

Z_KA=Z_KB=Z_KC=3U_A²/S_к^*.

Действительные части полных сопротивлений дадут величины сопротивлений резисторов, а мнимые - реактивные сопротивления конденсаторов.

По величине последних вычисляются емкости фазных конденсаторов, которые обеспечивают заданную величину коэффициента мощности второго потребителя, если в пределах его подключен компенсатор.

Таким образом, общий вид эквивалентной схемы компенсатора будет выглядеть так, как показано на рисунке 4.

Рис.4

5. Расчет трехфазной сети при улучшенном компенсатором коэффициенте мощности второго приемника.

Из практики известно, что компенсаторы включаются параллельно с той нагрузкой, характер которой и требует его подключения. В этой ситуации подключение компенсатора не окажет влияния на токи самого второго потребителя. Тем более такое подключение не скажется на режиме работы первого потребителя.

Таким образом, результаты предыдущих вычислений могут быть использованы в дальнейшем.

По известной схеме замещения компенсатора легко вычислить комплексы токов компенсатора. Ток фазы с компенсатора:

I_KC=S_к/3U_C.

Компенсатор для сети представляет собой симметричную нагрузку, поэтому токи других фаз могут быть записаны по найденной величине одного их токов.

Линейные токи второго потребителя с включенным компенсатором равны суммам соответствующих токов второго потребителя и компенсатора. Ток фазы В, например: I_2KB=I_2B+I_KB. Аналогично вычисляются и другие линейные токи. Для облегчения построения векторных диаграмм все вновь найденные токи должны быть записаны в комплексной форме.

6. Построение векторных диаграмм при подключенном компенсаторе.

Построение результирующей векторной диаграммы по известным комплексным действующим значениям токов и напряжений не представляет особого труда, но такая векторная диаграмма из-за обилия векторов может потерять наглядность.

Для наглядности предлагается построить три векторные диаграммы:

а) векторную диаграмму токов и напряжений второго потребителя и компенсатора;

б) векторную диаграмму напряжений и линейных токов источника, первого потребителя и суммарных линейных токов второго потребителя с подключенным компенсатором;

в) векторную диаграмму фазного напряжения и всех линейных токов одной из фаз в зависимости от номера варианта.

Такой набор векторных диаграмм позволит понять основное назначение компенсатора и его роль в трехфазной сети.

При анализе векторных диаграмм следует особое внимание обратить на угол фазового сдвига между фазными напряжениями и соответствующими линейными токами источника. Сравнить их с соответствующими углами на векторной диаграмме трехфазной сети, работающей без компенсатора во втором потребителе. Для полной наглядности следует начертить результирующую развернутую схему трехфазной сети с подключенным компенсатором.

7. Вычисление результирующего коэффициента мощности всей цепи с подключенным компенсатором.

Вычисление результирующего коэффициента мощности всей сети не связано с какими-то трудностями, так как для этого достаточно вычислить суммарную полную мощность цепи, включающую первый, второй потребители и компенсатор.

S= S₁₊S₂₊S_к,

где S- полная мощность источника, S₁=P_1A+P_1B+P_1C - мощность первого потребителя, S₂- полная мощность второго потребителя без компенсатора, S_к=P_к+jQ_к - полная мощность компенсатора.

Полная мощность первого потребителя и второго потребителя с компенсатором:

,

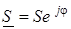и по известному аргументу комплекса полной мощности определяется коэффициент мощности.

8. Вычисление фазной ЭДС генератора.

В реальных условиях величина фазной ЭДС генератора больше соответствующего фазного напряжения сети. Это объясняется не только тем, что обмотки генератора имеют конечное омическое сопротивление или реактивное сопротивление, обусловленное потоком рассеивания, но и наличием явления называемого размагничивающим действием реакции якоря, смысл которого объясняется в теории синхронных генераторов.

В настоящей курсовой работе полное внутреннее сопротивление одной фазы генератора задано в форме активного сопротивления R_o и реактивного сопротивления Х_о. Таким образом, полное внутреннее сопротивление фазы генератора вычисляется в комплексной форме:

Z₀=R₀+jX₀.

Фазное сопротивление определено заданием и ранее записано в комплексной форме. В соответствии со вторым законом Кирхгофа для фазы А, например: E_A=Z₀I_A.

Используя ранее полученные комплексные действующие значения токов можно вычислить фазные ЭДС при подключенном компенсаторе второго потребителя или отсутствии компенсации второго приемника.

Полученные величины фазных ЭДС будут использоваться при рассмотрении переходных процессов в трехфазной цепи.

9. Расчет переходного процесса в трехфазной цепи.

Переходные процессы, то есть процессы перехода цепи из одного устойчивого состояния в другое устойчивое состояние, обусловлены переключениями различного рода или аварийными ситуациями. Динамика такого перехода может привести к дополнительным вторичным перенапряжениям в цепи или резким скачком тока, что неблагоприятно сказывается на режиме работы различной аппаратуры. Поэтому анализ переходных процессов в трехфазных цепях, как и в других цепях, имеет важное практическое значение.

В курсовой работе предлагается рассмотреть упрощенный вариант переходного процесса лишь в одной из фаз. Для упрощения цепи общие зажимы фазных сопротивлений второго потребителя и компенсатора условно соединяются нулевым проводом с соответствующим зажимом генератора.

В том случае, если фазные сопротивления нагрузки второго потребителя соединены “треугольником”, то для упрощения анализа необходимо заменить такое соединение эквивалентным соединением “звезда” на частоте 50 Гц.

В общем случае для такой эквивалентной замены можно воспользоваться известными уравнениями связывающие сопротивления «треугольника» и эквивалентной «звезды»:

.

В случае симметричной нагрузки Z_AB=Z_BC=Z_CA, поэтому:

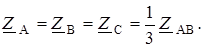
При эквивалентной замене для правильного начертания схемы цепи необходимо вычислить активное сопротивление и индуктивность катушки, которые при их последовательном соединении обеспечат на частоте 50 Гц соответствующее фазное сопротивление.

Для правильного определения закона изменения одной из величин в функции времени при переходном процессе необходимо начертить принципиальную схему цепи одной из фаз с учетом величины ранее вычисленной фазной ЭДС.

Возможно три варианта схем цепей, переходной процесс в которых подлежит рассмотрению: (Рис.5)

Рис.5

На рисунке 5,а изображен общий вид схемы цепи при подключении приемников к источнику питания. На рисунке 5,б представлена схема цепи для расчета переходного процесса в цепи, вызванного подключением компенсатора в сеть. На рисунке 5,в изображена схема цепи для расчета переходного процесса, вызванного частичным коротким замыканием фазной нагрузки, эквивалентным уменьшению фазного сопротивления в два раза. Частичные короткие замыкания возникают обычно при выходе из строя трехфазных двигателей.

Для анализа переходных процессов в цепях при мгновенных переключениях обычно используют или классический или операторный методы расчета. В дальнейшем даются лишь некоторые рекомендации для правильного нахождения закона изменения одной из величин в функции времени.

а) Пояснения и рекомендации к использованию классического метода расчета переходных процессов.

Классический метод расчета заключается в составлении системы дифференциальных уравнений на основании первого и второго законов Кирхгофа и последующим нахождением решения этой системы.

Для правильной записи системы дифференциальных уравнений необходимо, прежде всего, задаться положительным направлением токов ветвей и положительным направлением обхода выбранных независимых контуров. Контуры рекомендуется выбирать таким образом, чтобы в них входило минимальное количество реактивных элементов. После чего составляются уравнения по первому и второму законам Кирхгофа в дифференциальной форме.

Ниже приводится система дифференциальных уравнений для схемы изображенной на рисунке 5,б. Следует напомнить о том, что система уравнений составляется для состояния цепи после коммутации. Для рассматриваемого случая при замкнутом ключе “К”:

Предполагается во всех случаях, что переключения в цепи происходят в момент времени, равном нулю.

Решением данной системы является совокупность токов изменяющихся во времени по закону:

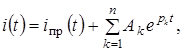
где: i_пр(t) - принужденная составляющая искомого тока, n - порядок характеристического уравнения, p_k–к-ый корень характеристического уравнения, A_k – к-ая постоянная, значение которой находится из граничных условий.

На первом этапе расчета следует вычислить и записать в функции времени принужденную составляющую искомой величины, для чего могут быть использованы результаты предыдущих расчетов.

На втором этапе записывается характеристическое уравнение системы, и находятся его корни p₁, p₂, p₃ и т.д.

В электротехнике используются два способа записи характеристического уравнения.

Первый способ заключается в записи матрицы коэффициентов при переменных в так называемой операторной форме. При этом операция дифференцирования заменяется умножением переменной на оператор р, а операция интегрирования делением переменной на оператор. Тогда искомая матрица записанной ранее системы будет выглядеть так:

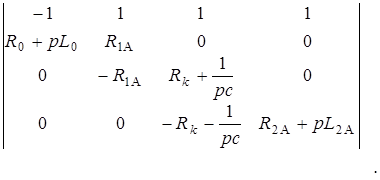
Записав определитель этой матрицы в общем виде и приравняв его нулю, получают характеристическое уравнение системы.

Второй способ заключается в следующем. Из схемы цепи, соответствующей ее состоянию после коммутации, исключается источник питания путем его замены внутренним сопротивлением. Обрывается любая ветвь цепи и записывается входное или эквивалентное сопротивление цепи относительно полученных зажимов в комплексной форме в функции (jw). В полученном выражении (jw) заменяется оператором р, и оно приравнивается нулю.

Для приведенного выше примера характеристическое уравнение будет выглядеть следующим образом:

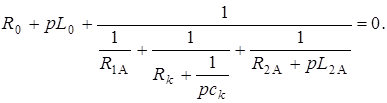
После несложных алгебраических преобразований получают характеристическое уравнение в форме, удобной для нахождения корней. Очевидно то, что в приведенном примере будет иметь место уравнение третьего порядка.

Наиболее сложным в расчете переходных процессов является нахождение постоянных А₁, А₂, А₃ и т.д. искомой величины. Для их вычисления используется система уравнений следующего вида (для нахождения тока i_1А, например): при n=3:

В приведенной системе известными являются ранее найденные корни характеристического уравнения p₁, p₂, p₃. Не составляет труда нахождение принужденного значения производных искомой величины при t=0. Ведь ранее был найден закон изменения принужденного значения искомой величины в функции времени.

Значения i_1А(0), di_1A(0)/dt и d²i_1A(0)/dt² находятся из системы дифференциальных уравнений, записанных для момента времени

t=0 с использованием законов коммутации. Для этого необходимо рассчитать токи индуктивностей и напряжений на конденсаторах для состояния ее перед коммутацией. Следует отметить, что для этого можно воспользоваться результатами предыдущих расчетов.

Получив значения i_L(0^–) и u_C(0^–) на основании законов коммутации из системы уравнений (при необходимости путем дополнительного дифференцирования уравнений) можно найти значения искомой величины и ее производных при t=0.

Общий вид системы уравнений при t=0 приведен ниже:

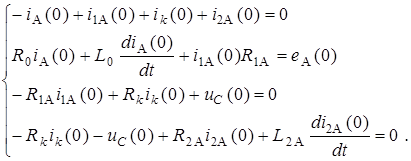
На основании законов коммутации в приведенной системе известными будут являться токи ветвей, содержащих индуктивности и напряжение на конденсаторе, то есть i_A(0); i_2A(0); и u_С(0) и, естественно, е_А(0). Решая совместно первое и третье уравнения, можно найти i_1A(0) и i_к(0); из второго уравнения находится значение di_A(0)/dt; из четвертого уравнения di_2A(0)/dt. После дополнительного дифференцирования уравнений при необходимости определяются и другие величины.

Подставляя полученные значения искомой величины и ее производных в систему уравнений для вычисления постоянных А₁, А₂, А₃, находят решение системы и записывают искомую величину в функции времени.

О способе нахождения постоянных А₁, А₂, А₃ более подробную информацию можно найти в учебниках или в теоретическом курсе.

Применение операторного метода расчета переходных процессов не всегда облегчает задачу нахождения искомой величины. Основными этапами расчета являются:

а) расчет цепи до коммутации для определения токов, индуктивностей и напряжений на зажимах конденсатора до замыкания ключа;

б) запись параметра источника питания в операторной форме;

в нашем случае не следует забывать о том, что фазная э.д.с. изменяется по синусоидальному закону во времени. Для записи ее изображения следует воспользоваться таблицей типовых изображений;

в) получение схемы цепи в операторной форме;

г) расчет цепи в общем виде с целью получения изображения искомой величины;

д) разложение полученного выражения на простые слагаемые дроби;

е) переход от изображения искомой величины к ее оригиналу с использованием таблиц оригиналов и изображений. Наиболее сложным при таком подходе является приведение изображения к виду, удобному для разложения на простые дроби и само разложение.

Примечание: решить систему дифференциальных уравнений, равно как и найти корни характеристического уравнения можно с помощью персональных компьютеров.

10. Построение временной диаграммы найденной величины.

По полученному закону изменения искомой величины во времени следует построить временную диаграмму. Для этого необходимо правильно выбрать масштабы изображения. Желательно масштаб времени выбрать таким образом, чтобы на графике получили изображение не менее трех периодов принужденного значения, или чтобы в представленном отрезке времени переходный процесс практически закончился.

11. Анализ результатов расчетов

В задании уже даны рекомендации о том, на что необходимо обратить внимание при анализе результатов расчетов. При анализе результатов расчета переходных процессов рекомендуется обратить внимание на соотношения максимальных значений величины, вызванных переходным процессом и принужденных значений, а также на длительность переходного процесса.