
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Анализ сложных цепей постоянного тока.
Вопросы:
- Расчёт методом непосредственного применения закона Кирхгофа.
- Расчёт методом контурных токов.
- Расчёт методом суперпозиции.
- Расчёт методом узловых напряжений.
- Расчёт методом эквивалентного генератора.
Ход лекции:
I. Расчёт методом применения закона Кирхгофа.
- Определяем кол-во узлов и ветвей.

- Произвольно зададим направление токов всех ветвей.
- Составляем уравнение по первому закону Кирхгофа для каждого независимого узла: k-1=3.
Для точки А: I1-I3-I2=0
Для точки В: I3+I5-I4=0
Для точки D: I4-I1+I67=0
- Недостающие уравнения: m-(k-1)=3 составляем по второму закону Кирхгофа для каждого независимого контура:
E1=I3R3+I4R4+I1R1
E2-E5= -I3R3+I2R2+I5*0
E5= I67(R6+R7)-I4R4
- Решая систему уравнений находим неизвестные токи в ветвях.
- По результатам полученных численно значений токов выполняем действия:
1). Уточняем направление тока в ветвях: если ток отрицательный, то пишем примечание – реальное направление тока противоположено показанному на схеме.
2). Определяем режим работы источника питания: если направление ЭДС и реального тока совпадают, то режим источника питания – режим генератора, если направление ЭДС и реального тока противоположно, то это режим потребителя.
7. Проверка решения – проверка уравнения баланса мощностей: алгебраическая сумма мощностей источников равна арифметической сумме мощностей нагрузок
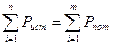
Если направление ЭДС и реального тока совпадают, то Рист=EI (>0), если направление ЭДС и реального тока не совпадают, то Рист= -EI (<0).
Можность нагрузки Рпотр=In2Rn
Итак, уравнение баланса мощностей для нашей схемы:
E1I1+E2I2-E5I5=I12R1+I22R2+I32R3+I24R4+I267(R6+R7)
Итак, если поле подстановки численных значений величин уравнения баланса обращается в тождество, то задача решена верно.
Достоинство метода: Его простота.
Недостатки метода:Большое количество совместно решаемых уравнений для сильно разветвленных цепей.
Поэтому метод применяется для расчета сложных цепей на компьютерах, в ручную не рекомендуется.
II. Расчёт методом контурных токов.

- Определение кол-ва узлов К=4, m=6
- Находим независимые контуры и для каждого задаётся произвольно положительное направление контурного тока. Контурный ток –ток, обтекающий ветви своего независимого контура.
- Составляем уравнения по второму закону Кирхгофа , учитывая все контурные токи, протекающие по ветвям выбранного контура.
I: E1=Ik1I(R1+R3+R4)-Ik2R3-Ik3R4
II: E2-E5=Ik2(R2+R3)-R3Ik1-Ik3R5
III. E5= Ik3(R4+R6+R7)-Ik1R4-Ik20
- Решая систему уравнений например, методом Крамера, найдём контурные токи:
Ik1=Δ1/Δ Ik2= Δ2/Δ Ik3=Δ3/Δ
 Δ – коэффициент при контурных токах
Δ – коэффициент при контурных токах

R1+R3+R4 -R3 -R4
Δ= -R3 R2+R3 0
-R4 0 R4+R6+R7
Δ1, Δ2, Δ3 получают заменой к-того столбца на левую часть уравнений.
- Произвольно обозначаем направление токов в ветвях.
- Выражаем токи в ветвях через алгебраическую сумму прилегающих контурных токов: контурный ток, совпадающий с током в ветви, записывают с плюсом.
I1=Ik1 I4=Ik1-Ik3
I2=Ik2 I5=Ik2-Ik3
I3=Ik1-Ik2 I67=Ik3
- по полученным значениям уточняем реальные направления токов в ветвях и определяем режимы работ.
- Проверка режимов баланса мощностей.
Достоинства метода: более короткий алгоритм
Недостатки метода:необходимо знание этого алгоритма.
Область применения: очень широкая для расчёта тока в разветвленных ветвях.
III. Расчёт методом суперпозиции.
В электротехнике принцип суперпозиции проявляет себя как принцип независимости действия ЭДС. Согласно этому принципу каждая ЭДС возбуждает в любой ветви свою долю тока – частичный ток. Результирующий ток в ветви определяется как алгебраическая сумма частичных токов.

- Задаём произвольное направление тока в ветвях.
- Создаём первую частичную схему замещения: из исходной схемы замещения выбрасываем все источники ЭДС, кроме первого, но оставляем их внутреннее сопротивление. Находим частичные токи в ветвях методом свёртки схемы.

R34=R3+R4


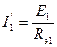
- Создаём вторую частичную схему замещения: выбрасываем все источники ЭДС, кроме второго и оставляем их внутренние сопротивления.
R34=R3+R4
Е2 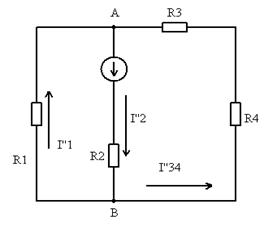

Rэ2=R2+R134

- Создаём третью частичную схему замещения аналогично прошлым.

R34=R3+R4
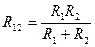
Rэ3 = R12+R34

- Наложив частичные схемы одну на другую, определяем результирующий ток в каждой ветви как алгебраическую сумму частичных токов.



Истинное направление токов на исходной схеме замещения определяем по результатам аналитического расчёта по правилу:
Если значение тока положительно, то направление тока угадано верно, если значение тока отрицательно, то реальное направление тока противоположно.
Алгоритм метода прост, требует знание только закона Ома, однако не производительный, поэтому для полного анализа сложной электрической цепи не применяется. Рекомендуется для частичного анализа цепи.
IV. Расчёт методом узловых напряжений.
В приложении для цепи с параллельными ветвями получил название «метод двух узлов».

- k=2, m=3
- Нахождение токов всех ветвей: Задаём произвольно условно положительное направление узлового напряжения между узлами и определяем его по формуле:
 , где
, где 
Узловое напряжение равно дроби, в числителе которого алгебраическая сумма произведений ЭДС на проводимости активных ветвей, а в знаменателе сумма проводимости всех ветвей.

- Определяем токи всех ветвей или заданной ветви, записывая уравнение второго закона Кирхгофа для каждой ветви и приложенного к ней узлового напряжения:

 E1=UAB+I1R1
E1=UAB+I1R1 
 -E2=UAB+I2R2
-E2=UAB+I2R2 
 0=UAB+I3R3
0=UAB+I3R3 

4. Проверка: Уравнение баланса мощностей: 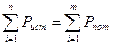

Достоинства:1. краткий алгоритм
2. метод как для полного, так и для частичного анализа
Недостаток: надо знать специфику алгоритма
Дата добавления: 2015-04-16; просмотров: 293; Мы поможем в написании вашей работы!; Нарушение авторских прав |