Метод узловых потенциалов (напряжений)

Методом узловых потенциалов составляются и решаются уравнения только первого закона Кирхгофа. Все источники ЭДС преобразуются в эквивалентные источники тока. Метод эффективно используется тогда, когда мало узлов, но много ветвей. Если число уравнений первого закона Кирхгофа меньше числа уравнений второго закона Кирхгофа, то этот метод более эффективен, но используется гораздо реже метода контурных токов.

Заземлим один зажим и найдем токи ветвей (рис. 2.7), считая известными потенциалы узлов и проводимости ветвей:

Составим уравнения первого закона Кирхгофа:

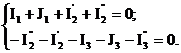
В полученные уравнения подставим заранее найденные токи:

(2.11)

Из уравнений (2.11) сформируем уравнения узловых потенциалов:

(2.12)

Рис. 2.7

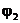Обозначим коэффициент при потенциале первого уравнения системы (2.12) , а коэффициент при второго уравнения - и назовем их узловыми проводимостями.

Из уравнений (2.12) видно, что узловые проводимости состоят из суммы проводимостей всех ветвей, принадлежащих узлу.

Остальные коэффициенты уравнений (2.12) называют межузловыми проводимостями и обозначают: и .

Узловые токи источников тока , равны соответственно правым частям уравнений (2.12).

С учетом введенных обозначений уравнения (2.12) примут вид:

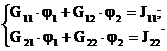(1.13)

Решение этих уравнений не вызывает затруднений.