
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Векторные диаграммы
Изображение гармонической величины в виде вектора
При расчете цепей переменного тока часто приходится суммировать (или вычитать) несколько однородных синусоидально изменяющихся величин одной и той же частоты ƒ, но имеющих разные амплитуды (Im , Em , Um) и начальные фазы (ψi , ψu , ψe ).
Такую задачу можно решать аналитическим путем тригонометрических преобразований или геометрически.
Геометрический метод более прост и нагляден, чем аналитический.
Синусоидальную величину (например, u = Um cos(ωt + ψu ) изображают в виде радиуса-вектора 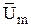 (см. рис.3.1), иногда просто Um или U, или вектором на комплексной плоскости Ủm – комплексная амплитуда или Ủ– комплексное действующее значение. Тогда между гармонической величиной и вектором на комплексной плоскости устанавливается взаимно однозначное соответствие, которое записывается в виде u→Umej(ωt+α) = ů-комплексное мгновенное значение.
(см. рис.3.1), иногда просто Um или U, или вектором на комплексной плоскости Ủm – комплексная амплитуда или Ủ– комплексное действующее значение. Тогда между гармонической величиной и вектором на комплексной плоскости устанавливается взаимно однозначное соответствие, которое записывается в виде u→Umej(ωt+α) = ů-комплексное мгновенное значение.
j

 ω
ω
Ủm
 ψ
ψ
 О + Рис. 3.1
О + Рис. 3.1
ψ – угол, образованный  Um с осью (+) в начальный момент времени, называемый начальной фазой. Вектор Um вращается в заданной плоскости вокруг точки О с постоянной угловой скоростью, равной угловой частоте ω, против часовой стрелки. Причем проекция этого вектора на ось «х» в любой момент времени и определеяет гармоническую величину Пр(Um)+ = Um cos(ωt + ψu). Направление вектора не указывает направление действия напряжение (или тока и э.д.с.). Это его отличие от векторов в механике, которыми обозначаются величина и направление силы, скорости, ускорения.
Um с осью (+) в начальный момент времени, называемый начальной фазой. Вектор Um вращается в заданной плоскости вокруг точки О с постоянной угловой скоростью, равной угловой частоте ω, против часовой стрелки. Причем проекция этого вектора на ось «х» в любой момент времени и определеяет гармоническую величину Пр(Um)+ = Um cos(ωt + ψu). Направление вектора не указывает направление действия напряжение (или тока и э.д.с.). Это его отличие от векторов в механике, которыми обозначаются величина и направление силы, скорости, ускорения.
Сумма двух синусоидальных величин изображается суммой векторов, изображающих отдельные слагаемые, а линейная комбинация нескольких синусоидальных величин – соответствующей линейной комбинацией векторов. Такое изображение синусоидальных величин называется векторной диаграммой. При построении векторных диаграмм один из векторов – исходный располагают произвольно, другие векторы – под соответствующими углами к исходному.
Пусть необходимо сложить две гармонические функции с одинаковым периодом, но разными начальными фазами (см.рис.3.2):
u1 = Um1 cos (ωt + α1) и u2 = Um2 cos (ωt + α2) .
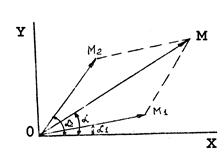
Рис.3.2
По известному правилу сложения векторов можно получить вектор  , изображающий сумму обеих функций u1(t) и u2(t), как геометрическую сумму векторов
, изображающий сумму обеих функций u1(t) и u2(t), как геометрическую сумму векторов 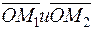 , изображающих эти функции. Все три векторы вращаются одновременно с угловой скоростью ω. Поэтому практически всегда изображают относительное расположение векторов и осей в момент t = 0.
, изображающих эти функции. Все три векторы вращаются одновременно с угловой скоростью ω. Поэтому практически всегда изображают относительное расположение векторов и осей в момент t = 0.
Геометрическое построение, описанное выше, определяет амплитуду ОМ = Um, фазу α
Часто нужно вычислять производную или интегралы гармонических функций времени типа u(t) = Umcos(ωt + α) . Имеем
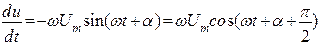
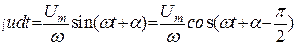 .
.
Дата добавления: 2015-04-16; просмотров: 247; Мы поможем в написании вашей работы!; Нарушение авторских прав |