Метод уравнений состояния

Как известно, переходный процесс в любой цепи определяется не только параметрами входящих в нее элементов, но и независимыми начальными (t=0₊) условиями — токами через индуктивности и напряжениями на емкостях в момент времени t=0₊, которые должны быть известны или рассчитаны. Через них выражают искомые величины во время переходного процесса. Они же определяют энергетическое состояние цепи. Поэтому в качестве переменных состояния выбирают токи и напряжения .

Действующие в цепи источники называются входными переменными , неизвестные функции — выходными . Для цепи с n независимыми токами и напряжениями должны быть заданы еще n независимых начальных условий.

Для линейных цепей система уравнений состояния является линейной и может быть записана в виде набора дифференциальных уравнений первого порядка, которые можно представить в виде матричного уравнения:

или в более компактной форме

,

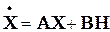где — квадратная матрица порядка n (основная); — матрица-столбец (размера ) переменных состояния (вектор переменных состояния); — матрица размера (матрица связи); — матрица-столбец (размера ) ЭДС и токов источников. Элементы этих матриц определяются топологией и параметрами цепи.

Расчет цепей методом переменных состояния можно разделить на два этапа:

1) составление системы дифференциальных уравнений цепи;

2) решение составленной системы дифференциальных уравнений.

Составить систему дифференциальных уравнений цепи можно различными способами, например, с применением метода наложения или непосредственно из системы уравнений, записанных по законам Кирхгофа, путем исключения токов и напряжений резистивных элементов. Однако совместное решение уравнений Кирхгофа при увеличении числа ветвей цепи становится все более громоздким.

Уравнения состояния можно формировать и сразу в матричной форме, как показано в [1].

Решение системы дифференциальных уравнений, составленных методом переменных состояния, можно выполнить как аналитически, так и численными методами.

При аналитическом решении уравнения состояния записываются в виде суммы матриц свободной — и принужденной — составляющих:

Здесь — соответствует переходному процессу (свободная составляющая) в цепи, обусловленному ненулевыми начальными условиями 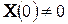при отсутствии внешних воздействий , —соответствует реакции цепи на внешние воздействия при нулевых начальных условиях ; — матрица (вектор) начальных значений переменных состояния, полученных при 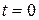; — матричная экспоненциальная функция.

Таким образом, если в цепи после коммутации нет источников энергии, т.е. , то решение матричного уравнения имеет вид

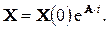
Если же после коммутации имеются источники независимых воздействий, то матрица и интегрирование матричного дифференциального уравнения 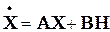приводит к решению в виде

.

Это решение состоит из суммы двух слагаемых — реакции цепи при ненулевых начальных условиях и реакции цепи при нулевых начальных условиях и наличии источников внешних воздействий .

Главная трудность расчета аналитическим методом заключается в вычислении матричной экспоненциальной функции. Матричную функцию вычисляют по формуле (теореме) Сильвестра [2]:

,

где , — собственные значения (характеристические числа) квадратной матрицы , , т.е. корни уравнения ,

где — единичная матрица порядка n.

Характеристические числа — это не что иное, как корни характеристического уравнения послекоммутационной схемы. Разложение матричной функции в представленный ряд предполагает, что характеристические числа различные (нет кратных корней).