Описание метода и экспериментальной установки. Определение показателя адиабаты для воздуха

Лабораторная работа 2.2.

Определение показателя адиабаты для воздуха

Методом Клемана-Дезорма.

Библиографический список

1. Трофимова Т. И. Курс физики. М.: Высшая школа, 1985.

2. Савельев И.В. Курс общей физики. – М.: Наука, 1988. Т. 1.

Цель работы: изучение газовых законов.

Приборы и принадлежности: прибор Клемана-Дезорма

Описание метода и экспериментальной установки

Величину показателя адиабаты ,
где:

С_p — теплоемкость газа при постоянном давлении,

В баллон при закрытом кране 2 накачивается воздух. При накачивании воздух, сжимаемый под поршнем насоса, нагревается, следовательно, необходимо выждать 2-3 минуты, пока благодаря теплообмену температура в баллоне не станет равной комнатной. Поле этого измеряют манометром избыточное давление воздуха p₁ (в миллиметрах столба жидкости, налитой в манометр). Давление в баллоне станет равным

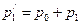
где p₀ – атмосферное давление; p₁ – избыток давления в баллоне над атмосферным давлением p₀, измеряемый манометром.

Открывают на короткое время кран 2, чтобы давление в баллоне сравнялось с атмосферным ( ), после чего закрывают кран.

Пусть масса воздуха после накачивания насосом в сосуде объемом V равна m. При открывании крана часть воздуха выходит. Обозначим массу вышедшего воздуха , тогда как масса оставшегося воздуха .

Масса воздуха , которая заключается в объеме V, занимала перед открытием крана меньший объем V₁. Так как процесс кратковременный и заметного теплообмена между газом и стенками нет, то его можно считать адиабатическим. Согласно уравнению Пуассона (для массы газа, равной ) получим:

(1)

Вследствие адиабатического расширения газа температура его понизилась, а затем в результате теплообмена температура газа через небольшой промежуток времени станет равной комнатной. При этом давление газа поднимается до величины

.

Начальное и конечное состояние газа наблюдается при одинаковой температуре. Поэтому на основании закона Бойля-Мариотта получим

(2)

Решая уравнения (1) и (2) относительно g, получаем

(3)

Разложим и в ряд Тейлора, ограничившись в этом случае двумя первыми членами:

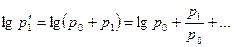
Подставляя эти значения в формулу (3), находим окончательно

(4)