
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные теоретические положения. Если цепь, содержащую параллельно соединённые приёмники Z1, Z2, Z3 (рис.3.1) подключить к источнику переменного синусоидального напряжения
Если цепь, содержащую параллельно соединённые приёмники Z1, Z2, Z3 (рис.3.1) подключить к источнику переменного синусоидального напряжения
u = Um sin ω t,
то токи всех приёмников также будут изменятся по синусоидальному закону, действующие значения которых можно определить по закону Ому:

Ток в неразветвлённой части цепи в комплексной форме определяется как алгебраическая сумма токов ветвей:

 |
Рис.3.1. Параллельное включение потребителей цепи синусоидального тока
Для схемы, изображенной на рис.3.1 векторная диаграмма строится следующим образом (рис.3.2).
Произвольно выбираем направление вектора напряжения U. Строим вектор I1, который совпадает с вектором напряжения U. К концу вектора I1 прибавляем вектор тока I2, который, в свою очередь, имеет активную Ia2 и реактивную Ip2 (индуктивную) составляющие. Активная составляющая вектора тока Ia2 совпадает с вектором напряжения U, реактивная Ip2 – отстаёт от вектора напряжения на угол 90˚. К концу вектора тока I2 прибавляем вектор тока I3 , который также имеет две составляющие: активная составляющая Ia3
Рис.3.2. Векторная диаграмма напряжений и токов
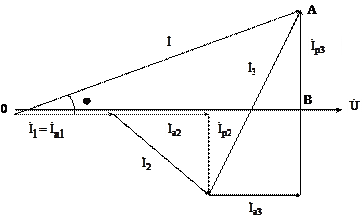 |
совпадает по фазе с вектором напряжения, реактивная (емкостная) Ip3 – опережает вектор напряжения на угол 90˚. Вектор тока в неразветвлённой части цепи I получим, соединив начало первого вектора I1 с концом третьего I3.
Ток I в неразветвлённой части цепи аналитически можно определить из треугольника OAB (рис.3.2) по теореме Пифагора:

где g1, g2, g3 – активные проводимости ветвей;
bL, bC – реактивные (индуктивная и емкостная) проводимости ветвей.
Для приёмников, имеющих активно – реактивный характер:

 |
Треугольники проводимостей и мощностей подобны треугольникам токов, но стороны этих треугольников – скалярные величины. Так для схемы рис.3.1 треугольники проводимостей и мощностей будут подобны треугольнику OAB (рис.3.2).
Рис.3.3. Треугольники проводимостей и мощностей
Если в параллельной цепи bL = bC , то полная проводимость:



Угол φ = 0, следовательно, ток и напряжение совпадают по фазе. Такой режим называют резонансом токов. Коэффициент мощности при резонансе cos φ = 1. В момент резонанса ток в неразветвлённой части цепи становится минимальным. На практике подключение конденсатора параллельно катушке индуктивности используют для повышения cos φ.
Дата добавления: 2015-04-16; просмотров: 207; Мы поможем в написании вашей работы!; Нарушение авторских прав |