Краткие теоретические сведения. В цепях переменного тока, кроме резисторов, часто включают катушки индуктивности и конденсаторы, которые при этом проявляют ряд свойств

В цепях переменного тока, кроме резисторов, часто включают катушки индуктивности и конденсаторы, которые при этом проявляют ряд свойств, отличающихся от свойств резисторов. Количественные оценки этих свойств выражают параметрами элементов цепей переменного тока, к которым относятся, кроме сопротивления резисторов R, индуктивность L, емкость С, а также индуктивное сопротивление X_L = ω ∙ L и емкостное сопротивление X_C = = 1 / (ω ∙ C), где ω – угловая частота (ω = 2 ∙ π ∙ f, f – частота переменного тока).

Характерным свойством резисторов является необратимое преобразование ими электрической энергии в тепловую, происходящее при протекании по ним тока.

В цепях переменного тока сопротивление резисторов называют активным. Данное сопротивление при этом для одного и того же резистора из-за влияния поверхностного эффекта имеет большее значение, чем электрическое сопротивление в цепях постоянного тока. Однако при сравнительно низких частотах этим различием обычно пренебрегают.

Напряжение, поданное на резистор, по фазе совпадает с током. Если ток через резистор изменяется по синусоидальному закону i = I_m ∙ sin(ω ∙ t), то напряжение будет изменяться аналогично u = U_m ∙ sin(ω ∙ t).

Индуктивность L, единицей измерения которой является генри (Гн), характеризует свойство катушки, при протекании по ней тока, накапливать энергию магнитного поля. В реальной цепи индуктивностью обладают и проводники, и реостаты, и конденсаторы. Однако их индуктивность часто мала, поэтому при расчетах в большинстве случаев учитывают только индуктивность катушек.

При протекании переменного тока через катушку индуктивности, которая содержит w витков, возникает переменный магнитный поток, наводящий в катушке, согласно закону электромагнитной индукции, ЭДС самоиндукции е_L = = w ∙ dФ / dt = ̶ L ∙ di / dt. Эта ЭДС влияет на величину тока, протекающего по катушке, что на практике учитывают путем введения понятия индуктивное сопротивление X_L = ω ∙ L, единицей измерения которого является Ом и значение которого пропорционально величине частоты. X_Lпри анализе цепей с помощью комплексного метода также называют модулем индуктивного сопротивления.

Максимальной скорости изменения тока катушки соответствует момент перехода синусоиды тока через нуль. При синусоидальной ЭДС это соответствует максимальному ее значению. С учетом отрицательного знака в формуле закона электромагнитной индукции данное обстоятельство говорит об отставании процесса изменения ЭДС от процесса изменения тока в идеальной катушке на 90⁰. Процесс изменения напряжения на индуктивности, наоборот, должен опережать процесс изменения тока в катушке, так как мгновенные значения ЭДС самоиндукции и напряжения имеют противоположные знаки.

При наличии в цепи переменного тока реальной катушки, имеющей, кроме индуктивного, еще и активное сопротивление, ток отстает по фазе от напряжения на угол ⱷ π/2.

Для упрощения анализа электрических цепей применяют комплексный метод.

При этом комплекс индуктивного сопротивления

X = ϳ ∙ ω ∙ L = ϳ ∙ X_L = X_L ∙ e ^{ϳ ∙ π / 2},

а комплекс полного сопротивления реальной катушки

Z = R + ϳ ∙ X_L= Z ∙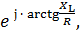

где Z – модуль полного сопротивления реальной катушки.

Емкость конденсатора, единицей измерения которой является фарад (Ф), характеризует его способность накапливать электрические заряды. На практике емкость существует между отдельными проводниками, между витками катушек, между проводниками и землей и т.д., но вследствие небольшой ее величины при анализе считают, что емкостью обладают только конденсаторы.

В диэлектрике, разделяющем пластины конденсатора, под воздействием приложенного к ним напряжения протекает ток электрического смещения i = dq / dt, где q – заряд на обкладках конденсатора, единицей измерения которого является кулон (К). Этот заряд пропорционален напряжению на конденсаторе q = C ∙ u_C. Поэтому

i = C ∙ du_c / dt.

Очевидно, что ток будет иметь максимальное значение при наибольшей скорости изменения напряжения, которая достигается в момент перехода кривой синусоидально изменяющегося напряжения через нуль. Из этого следует, что процесс изменения тока, протекающего через конденсатор, опережает процесс изменения напряжения на угол 90⁰. Причем напряжение, возникающее при накоплении зарядов на пластинах конденсатора, является фактором, уменьшающим ток через конденсатор, что чаще учитывают с помощью введения понятия емкостное сопротивление X_C = 1 / (ω ∙ C). При проведении комплексного анализа X_Cназывают также модулем емкостного сопротивления. Единицей измерения емкостного сопротивления также является Ом.

Комплекс емкостного сопротивления

X_C = 1 / (ϳ ∙ ω ∙ C) = ̶ ϳ / ( ω ∙ C) = ̶ ϳ ∙ X_C = X_C ∙ е ^{̶ ϳ ∙ π / 2}.

Полное комплексное сопротивление двухполюсника

Z = R + ϳ ∙ ( X_L ̶ X_C) = Z ∙ e^{ϳ ∙ arctg(X / R)},

где Z – модуль полного сопротивления цепи синусоидального тока;

Х = X_L ̶ X_C ̶ модуль реактивного сопротивления цепи.

Закон Ома для участка цепи в комплексной форме

I = U / Z ,

где U , I – комплексы напряжения и тока.

Мгновенная мощность двухполюсника

p = u ∙ i = U_m ∙ sin(ω ∙ t) ∙ I_m ∙ sin(ω ∙ t + ⱷ) =

(U_m ∙ I_m / 2)[cos ⱷ ̶ cos(2 ∙ ω ∙ t + ⱷ)].

Активная мощность двухполюсника

P = (1 / T) ∙ 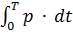= U ∙ I ∙ cos ⱷ.

Реактивная мощность двухполюсника

Q = U ∙ I ∙ sin ⱷ.

Полная мощность двухполюсника

S = U_m ∙ I_m / 2 = U ∙ I.

Комплексная мощность

S = U ∙ I^∙ = P ̶ ϳ ∙ Q = S ∙ e^{-ϳ ∙ arctg(Q / /P)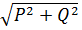} = ∙ e^{-ϳ ∙ arctg(Q / P)},

где I^∙ ̶ сопряженный комплекс тока.