
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач.
Пример 1
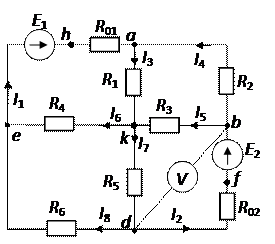 Дано: Е1 = 25 В;
Дано: Е1 = 25 В;
Е2 = 40 В;
R01 = R02 = 1 Ом;
R1 = R2 = R03 = 3 Ом;
R4 = R5 = R6 = 9 Ом.
Определить: показание вольтметра; КПД источников ЭДС; составить баланс мощности; построить потенциальную диаграмму для внешнего контура.
Преобразуем треугольники сопротивлений abk и dek в звезду:
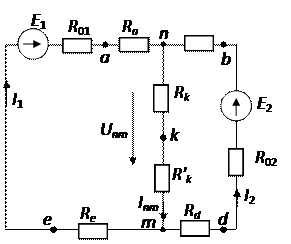 Пересчитаем сопротивление лучей звезды. Т.к. треугольники симметричные, то сопротивления лучей в з раза меньше сопротивлений сторон треугольников.
Пересчитаем сопротивление лучей звезды. Т.к. треугольники симметричные, то сопротивления лучей в з раза меньше сопротивлений сторон треугольников.
 Ом
Ом
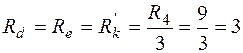 Ом.
Ом.
Для определения токов используем метод двух узлов:
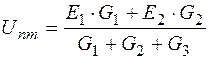 .
.
Проводимости ветвей
 см;
см;
 см;
см;
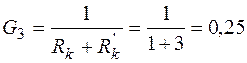 см.
см.
Токи в ветвях
 А;
А;
 А;
А;
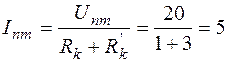 А.
А.
Для определения остальных токов в исходной схеме преобразуем треугольник сопротивлений dek в звезду. 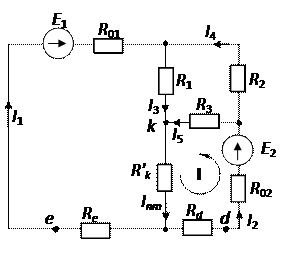
Запишем II закон Кирхгофа для контура I:
Е2 = I2(R02 + Rd) + I5R3 + InmRk’;
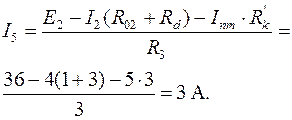
I4 = I2 – I5 = 4 – 3 = 1 А.
I3 = I1 + I4 = ! + ! = 2 А.
Запишем IIзакон Кирхгофа для контура I исходной схемы:
Е2 = I2R02 + I5R03 + I7R5;
I7 =  А;
А;
I8 = I7 – I2 = 3 – 4 = – 1 А;
I6 = I3 + I5 – I7 = 2 + 3 – 3 = 2 А;
Показание вольтметра:
U = E2 – I2R02 = 40 – 4 · 1 = 36 В;
КПД источников ЭДС:
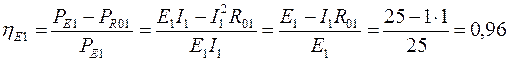 .
.
Баланс мощности:  ;
;
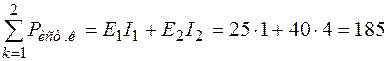 Вт;
Вт;

Для построения потенциальной диаграммы определяем суммарное сопротивление внешнего контура.
∑R = R2 + R02 + R6 + R01 = 3 + 1 + 9 + 1 = 14 Ом;
Принимаем потенциал т. «а» равным нулю (φа = 0)
φа – φa = –I4R2 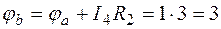 В;
В;
φb – φf = E2  В;
В;
φf – φd = – I2R02 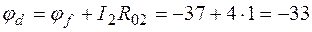 В;
В;
φd – φe = I8 · R6 φe = φd – I8 · R6 = – 33 + 1 · 9 = – 24 В;
φe – φh = – E1 φh = φe + E1= – 24 + 25 = 1 В;
 φh – φa = I1R01 φa = φh – I1R01 = 1 – 1 · 1 = 0.
φh – φa = I1R01 φa = φh – I1R01 = 1 – 1 · 1 = 0.
Ответ: U = 36 В; ηЕ1 = 0,96; ηЕ2 = 0,9.
Пример 2

Дано: законы изменения напряжения и тока на зажимах цепи
U = 282sin(314t + 60o) B;
i1 = 2,82sin(314t + 30o) A;
PR2 = 150 Вт; PR3 = 100 Вт;
QC2 = 200 ВАр; QL3 = 200 ВАр.
Определить: R1; R2; R3; L1; L3; C2; закон изменения тока i3; построить векторную диаграмму токов и напряжений.
Комплексная мощность приемника
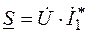 ;
;
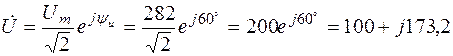 В;
В;
 А;
А;
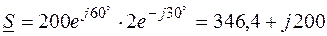 ВА;
ВА;
Р = 346,4 Вт; Q = 200 ВАр;
РR1 = P – PR2 – PR3 = 346,4 – 150 – 100 – = 96,4 Вт;
 Ом;
Ом;
Q = QL1 + QL3 – QC2 ;
QL1 = Q – QL3 + QC2 = 200 – 200 + 200 = 200 ВАр;
 Ом;
Ом;
 Гн = 159 Гн;
Гн = 159 Гн;
Напряжение 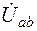 определяем по II закону Кирхгофа
определяем по II закону Кирхгофа
 ;
;
 ;
;
 Ом;
Ом;
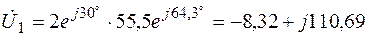 В;
В;
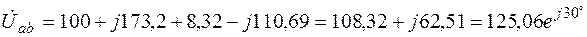 В;
В;
Токи в ветвях
 ;
;
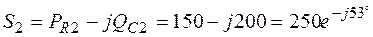 ВА;
ВА;
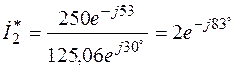 ;
;
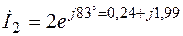 А;
А;
 ;
;
 ;
;
 ;
;
 ;
;
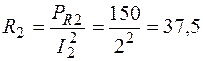 Ом;
Ом;
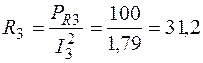 Ом;
Ом;
 Ом;
Ом;
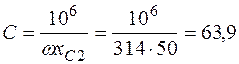 мкФ;
мкФ;
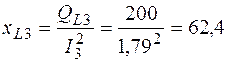 Ом;
Ом;
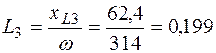 Гн = 199 мГн;
Гн = 199 мГн;
Закон изменения тока i3
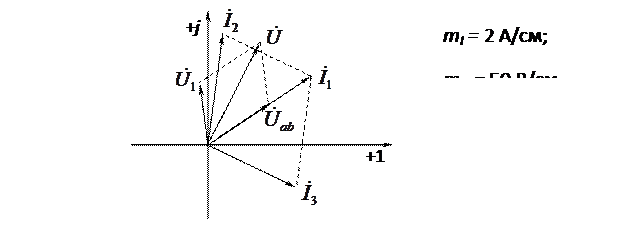
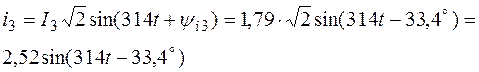
Ответ: R1 = 24,1 Ом; R2 = 37,5 Ом; R3 = 31,2 Ом; L1 = 159 мГн; L3 = 199 мГн; С2 = 63,9 мкФ; i3 = 2,52sin(314t – 33,4o) А.
Пример 3
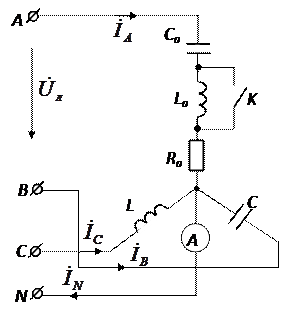
Дано: активная мощность приемника 290,4 Вт; R = 60 Ом;
L = 254,8 мГн;
С = 39,81 мкФ;
f = 50 Гц.
Определить: показание амперметра и коэффициент мощности приемника при замкнутом и разомкнутом ключе «К», изменение тока показать на векторной диаграмме.
Ключ «К» разомкнут.
Ток в фазе «А»
 А;
А;
 ,
, 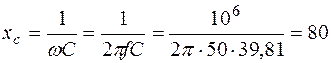 Ом;
Ом;
 Ом;
Ом;
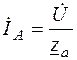 .
.
Фазное напряжение
Uф = IA · za;
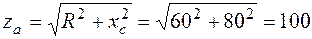 Ом;
Ом;
Uф = 2,2 · 100 220 В;
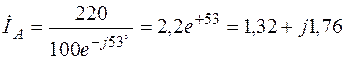 А;
А;
Ток в фазе «В»
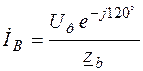 ;
;
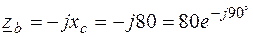 Ом;
Ом;
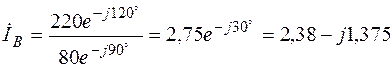 А;
А;
Ток в фазе «С»
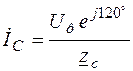 ;
;
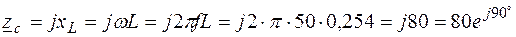 Ом;
Ом;
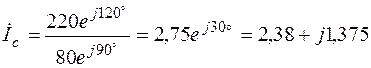 A;
A;
Ток в нейтральном проводе
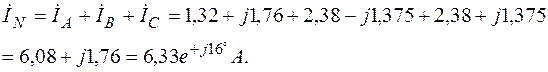
Показание амперметра – 63 А. Коэффициент мощности приемника 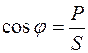 ;
;
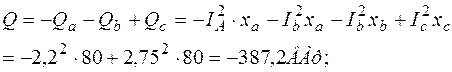
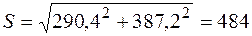 ВА;
ВА;

Ключ «К» разомкнут
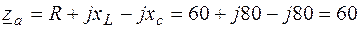 Ом;
Ом;
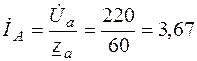 А.
А.
Токи в фазах «В» и «С» не изменятся.
Ток в нейтральном проводе:
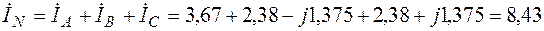 А;
А;
 Показание амперметра – 8,43 А. Коэффициент мощности приемника
Показание амперметра – 8,43 А. Коэффициент мощности приемника 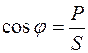 ;
;
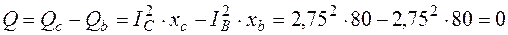 ;
;
S = P; cosφ = 1.
Ответ: IN = 6,33 А, cosφ = 0,6 при «К» замкнут;
IN = 8,43 А, cos φ = 1 при «К» разомкнут.
Пример 4

Дано: U = 20 В; R =2 Ом;
UНЭ1(I) = 1,21I2;
 UНЭ2 (I) = 0,7I2;
UНЭ2 (I) = 0,7I2;
UНЭ3(I) = 0,1I2.
Определить: показания приборов.
Нагрузочная характеристика строится по двум токам:
x.x: I = 0 → U = UНЭ123 = 20 В;
к.з: UНЭ123 = 0 → I к.з = 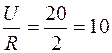 А.
А.
Ответ: I1 = 5,3 А; I2 = 2,3 А; I3 = 3 А; U = 2,7 В;
Р = U · I1 = 20 · 5,3 = 106 В.
Список
Дата добавления: 2015-04-16; просмотров: 304; Мы поможем в написании вашей работы!; Нарушение авторских прав |