
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольная работа № I
Задача 6.1. Воздух, имеющий начальное давление P1=0,1МПа и температуру t1=20°C, сжимается в одноступенчатом поршневом компрессоре до давления Р2. Сжатие может быть изотермическим, адиабатным и политропным с показателем политропы n. Определить для каждого процесса сжатия все начальные и конечные параметры воздуха, считая его идеальным газом; отведенную от воздуха теплоту Q, кВт и теоретическую мощность привода компрессора N, кВт, если производительность компрессора G, кг/с. Дать сводную таблицу и изображение процессов сжатия в pv- и Ts-диаграммах. Исходные данные выбрать из табл. 6.1.
Таблица 6.1.
Исходные данные к задаче 6.1.
| Последняя цифра шифра | n | Предпоследняя цифра шифра | P2, МПа | G, кг/с |
| 1,10 1,12 1,14 1,16 1,18 1,20 1,22 1,24 1,26 1,28 | 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 | 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 |
РЕШЕНИЕ (вариант 99). Для воздуха, как для идеального газа, принять: изохорную массовую теплоемкость Cv=0,72кДж/кг×К, газовую постоянную R=287Дж/кг×К, показатель адиабаты К=1,41. тогда начальный удельный объем воздуха по уравнению Клапейрона:
 .
.
Конечные температуры воздуха при изотермическом, адиабатном и политропном сжатиях соответственно:
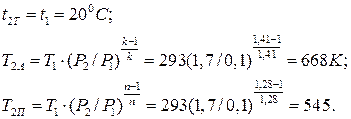
Конечные удельные объемы воздуха по уравнению Клапейрона:

Теплота, отведенная от воздуха, по уравнению теплового баланса:
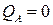 (процесс без теплообмена)
(процесс без теплообмена)
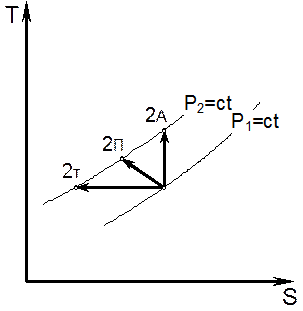 Рис. 6.2. TS-диаграмма процессов сжатия.
Рис. 6.2. TS-диаграмма процессов сжатия.
|
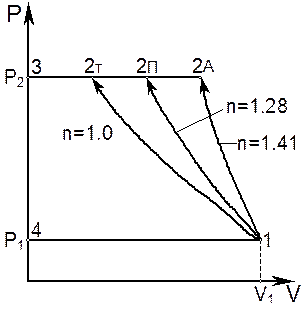 Рис. 6.1. Pv-диаграмма процессов сжатия.
Рис. 6.1. Pv-диаграмма процессов сжатия.
|
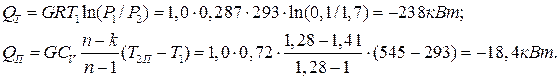
где знак (–) означает, что тепло отводится от сжимаемого воздуха.
Теоретические мощности привода компрессора:

что подтверждает вывод о том, что мощность привода изотермического компрессора минимальна, а адиабатного – максимальна.
Таблица 6.2
Сводная таблица рассчитанных величин
| Величина | Изотермическое сжатие | Адиабатное сжатие | Политропное сжатие |
| T2, К V2, м3/кг Q, кВт N, кВт | 0,0495 -238 | 0,1128 | 0,092 -18,4 |
Задача 6.2. Рассчитать теоретический цикл двигателя внутреннего сгорания (ДВС), считая, что рабочим тело является воздух с начальными параметрами P1 =0,1МПа, t1=20°С. Определить основные параметры рабочего тела P, V, T во всех точках цикла, изменение внутренней энергии DU, энтальпии Dh, энтропииDS для всех процессов и для цикла; теплоту и работу для процессов и для цикла, а также термический КПД цикла. Дать сводную таблицу и изобразить цикл в PV- и TS-диаграммах. Исходные данные брать из табл. 6.3.
Таблица 6.3
Исходные данные к задаче 6.2
| Последняя цифра шифра | Цикл | Степень сжатия, e | Предпо-следняя цифра шифра | Степень повыше-ния давления, l | Степень предвари-тельного расши-рения, r |
| Отто *) Дизеля **) Тринклера-Сабатэ | 2,4 2,3 2,2 2,1 2,0 1,9 1,8 1,7 1,6 1,5 | 2,1 2,0 1,9 1,8 1,7 1,6 1,5 1,4 1,3 1,2 |
Примечание: независимо от исходных данных принимать *) r=1 для циклов с изохорным подводом теплоты (цикл Отто) и **) l=1 для циклов с изобарным подводом теплоты (цикл Дизеля).
РЕШЕНИЕ (вариант 99). Для воздуха, как для идеального газа, принять: теплоемкости Cp=1,01кДж/(кгК) и Cv=0,72 кДж/(кгК); газовую постоянную R=287 Дж/(кгК), показатель адиабаты K=1,41. Для варианта 99 задан цикл ДВС со смешанным подводом теплоты (цикл Тринклера-Сабатэ).
Начальный удельный объем рабочего тела по уравнению Клапейрона:
 .
.
По степени сжатия e=v1/v2 находим удельный объем рабочего тела в точке 2
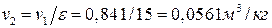 .
.
Процесс 1-2 – это адиабатное сжатие рабочего тела, а уравнение адиабатного процесса
 ,
,
Откуда находится давление в точке 2:
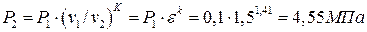 .
.
Температура в точке 2 находится по уравнению Клапейрона:
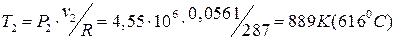 .
.
Для изохорного процесса подвода тепла к рабочему телу 2-3 характеристикой является степень повышения давления l=P3/P2, откуда находится давление в точке 3:
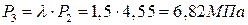 .
.
С учетом того, что для изохорного процесса v3= v2=0,0561м3/кг, температура рабочего тела в точке 3 по уравнению Клапейрона:
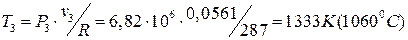 .
.
Для изобарного процесса подвода тепла к рабочему телу 3-4 характеристикой является степень предварительного расширения r= V4/V3, откуда находится удельный объем рабочего тела в точке 4:
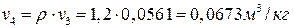 .
.
Для изобарного процесса P4=P3=6.82МПа, тогда температура рабочего тела в точке 4 по уравнению Клапейрона:
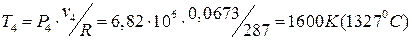
С учетом того, что процесс 5-I – это изохорный отвод тепла от рабочего тела,  . Тогда для адиабатного процесса расширения рабочего тела 4-5:
. Тогда для адиабатного процесса расширения рабочего тела 4-5: 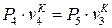 , откуда находится давление в точке 5:
, откуда находится давление в точке 5:
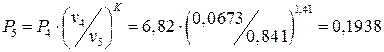 МПа.
МПа.
Температура рабочего тела в точке 5 по уравнению Клапейрона:
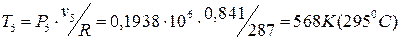 .
.
Параметры всех точек цикла сводим в табл. 6.4.
Таблица 6.4
Рассчитанные параметры точек цикла
| Параметры | Точки | ||||
| Давление Р, МПа | 0,1 | 4,55 | 6,82 | 6,82 | 0,1938 |
| Удельный объем n, м3/кг | 0,841 | 0,0561 | 0,0561 | 0,0673 | 0,841 |
| Температура Т, К | |||||
| Температура t, ºC |
Изменение внутренней энергии в процессах и для цикла в целом:
∆  ;
;
∆ 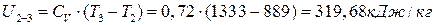 ;
;
∆ 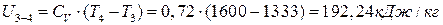 ;
;
∆ 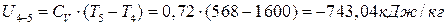 ;
;
∆  ;
;
∆ 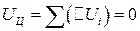 .
.
Суммарное изменение внутренней энергии в цикле ∆ 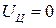 , что подтверждает правильность расчетов, так как
, что подтверждает правильность расчетов, так как
∆  .
.
Изменение энтальпии в процессах и для цикла в целом:
∆ 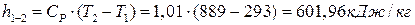 ;
;
∆ 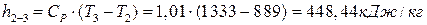 ;
;
∆ 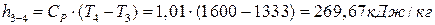 ;
;
∆ 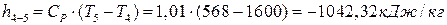 ;
;
∆ 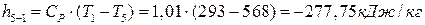 ;
;
∆  , действительно: ∆
, действительно: ∆ 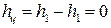 .
.
Изменение энтропии в процессах и для цикла в целом: 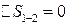 , так как это процесс адиабатный, то есть без теплообмена между рабочим телом и окружающей средой:
, так как это процесс адиабатный, то есть без теплообмена между рабочим телом и окружающей средой:
 ;
;
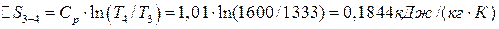 ;
;
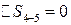 , так как это процесс адиабатный;
, так как это процесс адиабатный;
 ;
;
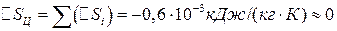 ,
,
что также подтверждает правильность расчетов, так как
 .
.
Работа процессов и цикла в целом
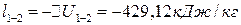 ,
,
так как это процесс адиабатный, то есть без отвода теплоты от рабочего тела, поэтому внутренняя энергия рабочего тела возрастает за счет теплоты сжатия, а знак “-” означает затрату работы на сжатие газа.
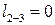 , так как в изохорном процессе нет измерения объема газа, следовательно, работа против внешних сил не совершается.
, так как в изохорном процессе нет измерения объема газа, следовательно, работа против внешних сил не совершается.
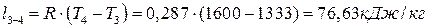 ;
;
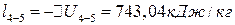 ;
;  .
.
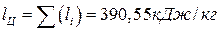 .
.
Теплота процессов и цикла в целом;  , так как это процесс адиабатный, то есть без теплообмена;
, так как это процесс адиабатный, то есть без теплообмена;
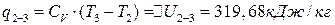 ;
;
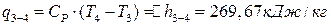 ;
;
 , так как это адиабатный процесс;
, так как это адиабатный процесс;

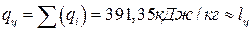 ,
,
что подтверждает правильность расчетов, так как для циклов 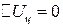 , следовательно, по I закону термодинамики
, следовательно, по I закону термодинамики 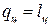 .
.
Термический КПД цикла представляет собой отношение работы цикла к подведенной к рабочему телу теплоте:
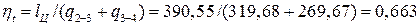 .
.
Проверка:
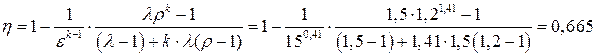
Погрешность расчета:
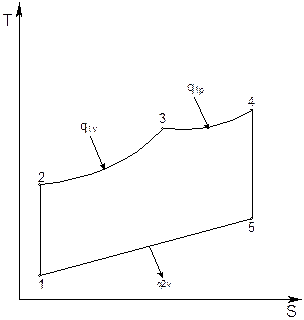 Рис. 6.4. TS-диаграмма цикла Тринклера-Сабатэ.
Рис. 6.4. TS-диаграмма цикла Тринклера-Сабатэ.
|
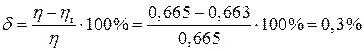 <1%, то есть точность расчета достаточная.
<1%, то есть точность расчета достаточная.
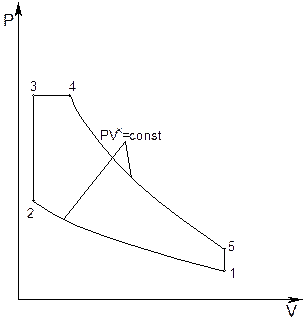 Рис. 6.3. Pv-диаграмма цикла Тринклера-Сабатэ.
Рис. 6.3. Pv-диаграмма цикла Тринклера-Сабатэ.
|
ЗАДАЧА 6.3. Определить эффективную мощность Ne газотурбинной установки (ГТУ) без регенерации теплоты и ее эффективный КПД по заданной степени повышения давления 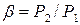 , известным адиабатным КПД турбины
, известным адиабатным КПД турбины  и компрессора
и компрессора 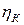 , температуре воздуха перед компрессором
, температуре воздуха перед компрессором 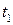 , температуре газа перед турбиной
, температуре газа перед турбиной 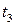 и по расходу воздуха через ГТУ
и по расходу воздуха через ГТУ 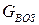 . Изобразить цикл ГТУ в PV- и TS- диаграммах. Показать, как зависит термический КПД ГТУ от степени повышения давления
. Изобразить цикл ГТУ в PV- и TS- диаграммах. Показать, как зависит термический КПД ГТУ от степени повышения давления 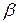 . Исходные данные выбрать из табл.6.5.
. Исходные данные выбрать из табл.6.5.
Таблица 6.5
Исходные данные к задаче 6.3
| Послед-няя цифра шифра | t1,ºC | t3, ºC | β | Предпос-ледняя цифра шифра | ηк | ηТ | 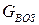 ,
кг/с ,
кг/с
|
| 7,2 9,0 8,8 8,5 8,2 8,0 7,5 7,0 6,5 6,2 | 0,82 0,81 0,79 0,82 0,81 0,80 0,79 0,78 0,77 0,76 | 0,89 0,88 0,85 0,87 0,86 0,84 0,82 0,86 0,83 0,85 |
РЕШЕНИЕ (вариант 99). В расчете принимать теплоемкость воздуха и газа Ср=1,01кДж/(кгК); показатель адиабаты К=1,41; механический КПД ГТУ ηм=0,98; давление воздуха перед компрессором Р1=0,1 МПа.
Удельный объем воздуха перед компрессором по уравнению Клапейрона:
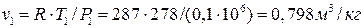 .
.
Температура воздуха после компрессора при адиабатном теоретическом сжатии по уравнению адиабатного процесса:
 ;
;
 ,
,
а при действительном адиабатном сжатии – из выражения внутреннего адиабатного КПД компрессора:
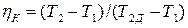 ;
;
 .
.
Давление сжатого воздуха в компрессоре
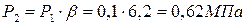 .
.
Удельные объемы воздуха в точках 2, 2Д, 3 по уравнению Клапейрона:
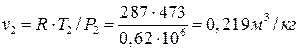 ;
;
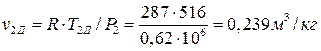 ;
;
 .
.
Температура газов после газовой турбины при адиабатном теоретическом расширении
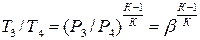 ;
;
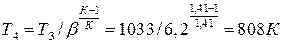 ,
,
а при действительном адиабатном расширении – из выражения внутреннего адиабатного КПД газовой турбины
 ;
;
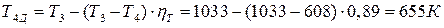 .
.
Удельные объемы газа в точках 4 и 4Д по уравнению Клапейрона:
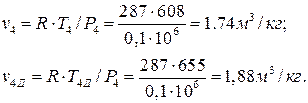
Для построения цикла ГТУ в TS – диаграмме необходимо определить изменения энтропии в процессах:

Эффективная работа ГТУ:

Эффективный КПД ГТУ:
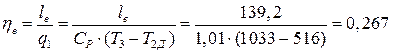 .
.
Эффективная мощность ГТУ:
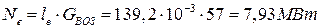 .
.
Зависимость термического КПД цикла ГТУ от степени повышения давления определялась по выражению
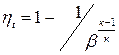 ,
,
результаты расчетов по которому представлены в табл.6.6.
Таблица 6.6
Зависимость термического КПД цикла
без регенерации теплоты от степени повышения
давления
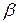
| 6,2 | ||||
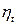
| 0,374 | 0,412 | 0,432 | 0,454 | 0,472 |
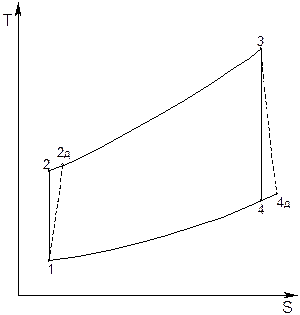 Рис. 6.6. TS-диаграмма ГТУ без регенерации теплоты.
Рис. 6.6. TS-диаграмма ГТУ без регенерации теплоты.
|
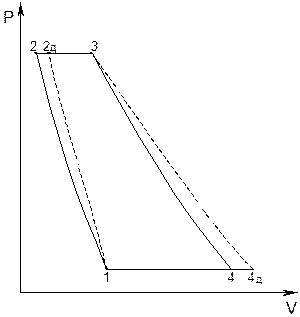 Рис. 6.5. Pv-диаграмма ГТУ без регенерации теплоты.
Рис. 6.5. Pv-диаграмма ГТУ без регенерации теплоты.
|
Из табл. 6.6 следует, что термический КПД возрастает с увеличением степени повышения давления в компрессоре.
ЗАДАЧА 6.4. Определить термический КПД цикла Ренкина и эффективную мощность паротурбинной установки (ПТУ) по заданным начальному давлению Р1 и температуре перегретого пара перед турбиной t1; конечному давлению в конденсаторе Р2 , расходу пара через турбину D, внутренним относительным КПД турбины ηТ и питательного насоса ηН. Изобразить цикл Ренкина в TS – диаграмме, а процессы сжатия воды в питательном насосе и расширения пара в турбине – в hS – диаграмме. Механический КПД ПТУ принять равным ηМ=0,98. Исходные данные выбрать из табл.6.7.
Таблица 6.7
Исходные данные к задаче 6.4
| Послед-няя циф-ра шифра | Р1, МПа | t1, ºC | ηТ | Предпос-ледняя цифра шифра | Р2, кПа | D, кг/с | ηН |
| 10,0 | 0,80 | 3,0 | 0,70 | ||||
| 10,5 | 0,81 | 3,5 | 0,71 | ||||
| 11,0 | 0,82 | 4,0 | 0,72 | ||||
| 11,5 | 0,83 | 4,5 | 0,73 | ||||
| 12,0 | 0,84 | 5,0 | 0,74 | ||||
| 12,5 | 0,85 | 3,0 | 0,75 | ||||
| 13,0 | 0,86 | 3,5 | 0,76 | ||||
| 13,5 | 0,87 | 4,0 | 0,77 | ||||
| 14,0 | 0,88 | 4,5 | 0,78 | ||||
| 14,5 | 0,89 | 5,0 | 0,79 |
РЕШЕНИЕ (вариант 99). Решение может быть выполнено с помощью hS – диаграммы водяного пара (приближенное) или с помощью таблиц термодинамических свойств воды и водяного пара (точное).
На рис. 6.7…6.9 изображены процессы в паротурбинной установке: 1-2 – теоретическое адиабатное расширение пара в турбине; 1-2Д – действительное расширение пара; 2- 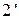 – изобарно-изотермическая конденсация пара в конденсаторе;
– изобарно-изотермическая конденсация пара в конденсаторе; 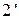 -3 – теоретическое адиабатное сжатие воды в питательном насосе;
-3 – теоретическое адиабатное сжатие воды в питательном насосе; 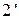 -3Д – действительное сжатие воды (в TS – диаграмме эти процессы не отражены, ввиду малого изменения параметров воды в этих процессах; они изображены в увеличенном масштабе в hS – диаграмме на рис. 6.8); 3Д-4 – изобарный нагрев воды до температуры насыщения в водяном экономайзере; 4-5 – изобарно-изотермическое парообразование в парогенераторе; 5-1 – изобарный перегрев пара в пароперегревателе.
-3Д – действительное сжатие воды (в TS – диаграмме эти процессы не отражены, ввиду малого изменения параметров воды в этих процессах; они изображены в увеличенном масштабе в hS – диаграмме на рис. 6.8); 3Д-4 – изобарный нагрев воды до температуры насыщения в водяном экономайзере; 4-5 – изобарно-изотермическое парообразование в парогенераторе; 5-1 – изобарный перегрев пара в пароперегревателе.
Точка I в hS –диаграмме находится на пересечении изобары Р1 = 145 бар и изотермы t1 = 590º C, для которой находится энтальпия перегретого пара перед турбиной h1 = 3586 кДж/кг. Теоретическое расширение пара в турбине 1-2 изображается вертикальной линией S2 = S1 до пересечения с изобарой Р2 = 0,05 бар, откуда в точке 2 находится энтальпия пара после турбины h2 = 2035 кДж/кг.
Ниже приведены таблицы 6.8 и 6.9 термодинамических свойств воды и водяного пара, с помощью которых задача решается более точно. Критические параметры воды: Ркр = 221,29 бар; tкр = 374,15 º C; vкр = 0,00326 м3/кг; hкр = 2100 кДж/кг; Sкр = 4,43 кДж/(кгК).
Из табл. 6.9 свойств перегретого пара для давления Р1 = 145 бар и температуры t1 = 590º C находим методом линейной интерполяции энтальпию h1 = 3554 кДж/кг и энтропию перегретого пара перед турбиной S1 = 6,67 кДж/(кгК).
Теоретическое адиабатное расширение пара происходит при постоянной энтропии S2 = S1 = 6,67 кДж/(кгК) до давления Р2 = 0,05 бар. Из hS – диаграммы процесса на рис. 6.9 видно, что состояние пара после турбины (в точке 2) соответствует влажному насыщенному пару, для которого энтропия находится по формуле:
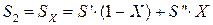 ,
,
где энтропия воды на линии насыщения при давлении Р2 = 0,05 бар по табл. 6.8  = 0,4761 кДж/(кгК) и энтропия сухого насыщенного пара
= 0,4761 кДж/(кгК) и энтропия сухого насыщенного пара 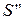 = 8,393 кДж/(кгК). Тогда степень сухости влажного пара после турбины (в точке 2):
= 8,393 кДж/(кгК). Тогда степень сухости влажного пара после турбины (в точке 2):
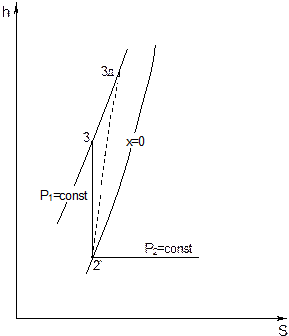 Рис. 6.8. Процессы теоретического 2´-3 и действительного 2´-3Д сжатия воды в питательном насосе.
Рис. 6.8. Процессы теоретического 2´-3 и действительного 2´-3Д сжатия воды в питательном насосе.
|
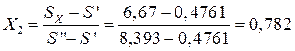 .
.
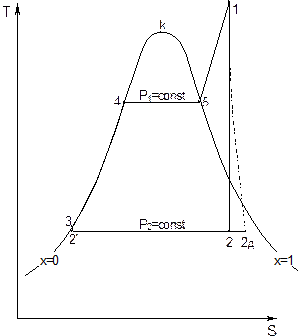 Рис. 6.7. Цикл Ренкина в TS-диаграмме.
Рис. 6.7. Цикл Ренкина в TS-диаграмме.
|

Рис. 6.9. Процессы расширения пара в турбине: 1-2- - теоретический; 1-2Д – действительный.
Таблица 6.8
Таблица термодинамических свойств сухого насыщенного пара
и воды на линии насыщения
| РН, бар | tH, º C | 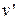 ,
м3/кг ,
м3/кг
| 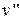 ,
м3/кг ,
м3/кг
| 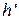 ,
кДж/кг ,
кДж/кг
|  ,
кДж/кг ,
кДж/кг
| r, кДж/кг |  ,
кДж/(кгК) ,
кДж/(кгК)
| 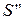 ,
кДж/(кгК) ,
кДж/(кгК)
|
| 0,010 | 6,92 | 0,001000 | 129,9 | 29,3 | 0,1054 | 8,975 | ||
| 0,025 | 21,09 | 0,001002 | 54,24 | 88,5 | 0,3124 | 8,642 | ||
| 0,050 | 32,88 | 0,001005 | 28,19 | 137,8 | 0,4761 | 8,393 | ||
| 0,075 | 40,32 | 0,001008 | 19,23 | 168,8 | 0,5764 | 8,250 | ||
| 0,100 | 45,84 | 0,001010 | 14,68 | 191,9 | 0,6492 | 8,149 | ||
| 1,00 | 99,64 | 0,001043 | 1,694 | 417,4 | 1,3026 | 7,360 | ||
| 10,0 | 179,88 | 0,001127 | 0,1946 | 762,7 | 2,138 | 6,587 | ||
| 263,91 | 0,001286 | 0,0394 | 2,921 | 5,973 | ||||
| 303,32 | 0,001417 | 0,0205 | 3,287 | 5,678 | ||||
| 310,96 | 0,001452 | 0,0180 | 3,360 | 5,615 | ||||
| 318,04 | 0,001489 | 0,0160 | 3,430 | 5,553 | ||||
| 324,63 | 0,001527 | 0,0143 | 3,496 | 5,492 | ||||
| 330,81 | 0,001567 | 0,0128 | 3,561 | 5,432 | ||||
| 336,63 | 0,001611 | 0,0115 | 3,623 | 5,372 | ||||
| 342,11 | 0,001658 | 0,0104 | 3,684 | 5,310 | ||||
| 347,32 | 0,001710 | 0,0093 | 3,746 | 5,247 |
Таблица 6.9
Таблица термодинамических свойств перегретого пара
| Р, бар | ||||||||||
| t, º C | n, м3/кг | h, кДж/кг | S, кДж/(кгК) | n, м3/кг | h, кДж/кг | S, кДж/(кгК) | n, м3/кг | h, кДж/кг | S, кДж/(кгК) | |
| 0,000999 0,001011 0,001042 0,001089 0,001156 | 2,1 210,9 420,1 632,8 852,4 | 0,0000 0,7020 1,3048 1,838 2,328 | 0,000999 0,001011 0,001042 0,001089 0,001155 | 3,1 211,8 420,9 633,4 852,6 | 0,0000 0,7018 1,3038 1,837 2,326 | 0,000998 0,001009 0,001041 0,001088 0,001153 0,001249 | 5,2 213,6 422,5 634,7 853,6 | 0,0004 0,700 1,302 1,835 2,322 2,789 | ||
| 0,1114 0,1255 0,1384 0,1511 0,1634 0,1755 0,1875 0,1995 0,2114 0,2232 | 6,539 6,757 6,949 7,122 7,282 7,429 7,569 7,701 7,827 7,947 | 0,0707 0,0812 0,0905 0,0993 0,1078 0,1161 0,1243 0,1325 0,1405 0,1484 | 6,283 6,530 6,735 6,916 7,080 7,231 7,373 7,506 7,633 7,755 | |||||||
| 0,0454 0,0519 0,0578 0,0633 0,0686 0,0737 0,0787 0,0836 0,0884 | 6,200 6,440 6,640 6,815 6,974 7,120 7,257 7,387 7,510 |
Окончание табл.6.9
| Р, бар | |||||||||
| t,º C | n, м3/кг | h, кДж/кг | S, кДж/(кгК) | n, м3/кг | h, кДж/кг | S, кДж/(кгК) | n, м3/кг | h, кДж/кг | S, кДж/(кгК) |
| 0,000996 | 8,2 | 0,0004 | 0,000995 | 10,2 | 0,0004 | 0,000993 | 15,2 | 0,0008 | |
| 0,001008 | 216,2 | 0,6992 | 0,001007 | 218,0 | 0,698 | 0,001005 | 222,3 | 0,695 | |
| 0,001040 | 424,9 | 1,3996 | 0,001038 | 426,5 | 1,298 | 0,001036 | 430,4 | 1,294 | |
| 0,001086 | 636,6 | 1,832 | 0,001084 | 638,0 | 1,830 | 0,001081 | 641,3 | 1,824 | |
| 0,001150 | 855,0 | 2,317 | 0,001148 | 856,0 | 2,314 | 0,001144 | 858,3 | 2,306 | |
| 0,001244 | 1085,7 | 2,781 | 0,001240 | 2,776 | 0,001233 | 2,765 | |||
| 0,02429 | 5,788 | 0,001397 | 3,244 | 0,001377 | 3,222 | ||||
| 0,03003 | 6,126 | 0,02247 | 5,940 | 0,01150 | 5,442 | ||||
| 0,03438 | 6,356 | 0,02646 | 6,207 | 0,01568 | 5,878 | ||||
| 0,03821 | 6,552 | 0,02979 | 6,416 | 6,139 | |||||
| 0,04177 | 6,722 | 0,03281 | 6,596 | 0,02080 | 6,346 | ||||
| 0,04516 | 6,876 | 0,03566 | 6,756 | 0,02291 | 6,521 | ||||
| 0,04844 | 7,019 | 0,03837 | 6,901 | 0,02490 | 6,677 | ||||
| 0,05161 | 7,152 | 0,04097 | 7,038 | 0,02677 | 6,822 | ||||
| 0,05475 | 7,280 | 0,04354 | 7,167 | 0,02857 | 6,956 |
Тогда энтальпия влажного пара после турбины
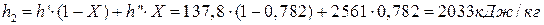 ,
,
где 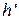 = 137,8 кДж/кг – энтальпия воды на линии насыщения и
= 137,8 кДж/кг – энтальпия воды на линии насыщения и  = 2561 кДж/кг – энтальпия сухого насыщенного пара, взятые также из табл. 6.8 при давлении Р2 = 0,05 бар.
= 2561 кДж/кг – энтальпия сухого насыщенного пара, взятые также из табл. 6.8 при давлении Р2 = 0,05 бар.
Необратимые потери при действительном расширении пара в турбине 1-2Д учитываются внутренним относительным КПД турбины
 ,
,
откуда, при заданном  = 0,89, находим энтальпию в конце действительного расширения пара:
= 0,89, находим энтальпию в конце действительного расширения пара:
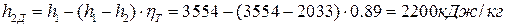 .
.
Степень сухости пара в точке 2Д:
 .
.
Энтропия пара в точке 2Д:
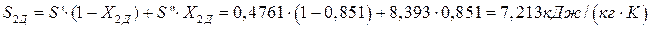 .
.
Повышение энтальпии питательной воды в насосе:
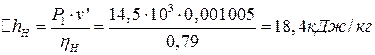 ,
,
где Р1 = 14,5·103 кПа – давление питательной воды после насоса; 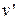 = 0,001005 м3/кг – удельный объем воды перед насосом (при Р2 = 0,05 бар);
= 0,001005 м3/кг – удельный объем воды перед насосом (при Р2 = 0,05 бар); 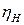 = 0,79 – внутренний относительный КПД насоса (задан).
= 0,79 – внутренний относительный КПД насоса (задан).
Энтальпия воды за питательным насосом:
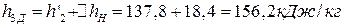 .
.
Внутренний относительный КПД насоса
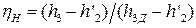 ,
,
откуда находим энтальпию питательной воды после теоретического сжатия:
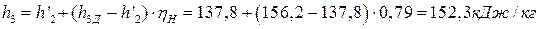 .
.
Процессы теоретического 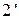 -3 и действительного
-3 и действительного 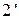 -3Д сжатия воды в питательном насосе изображены в hS – диаграмме на рис.6.8.
-3Д сжатия воды в питательном насосе изображены в hS – диаграмме на рис.6.8.
Термический КПД цикла Ренкина:
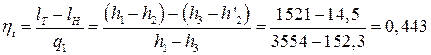 .
.
Так как работа пара в турбине
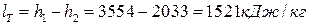
много больше работы сжатия воды в насосе.
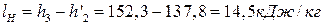 ,
,
то для приближенных расчетов работой сжатия воды в насосе пренебрегают ( 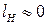 ), тогда приближенно:
), тогда приближенно:
 .
.
С учетом внутренних необратимых потерь в турбине и в насосе находим внутреннюю работу ПТУ:
 .
.
Теоретическая работа ПТУ:
 .
.
Следовательно, из-за необратимых потерь теряется работоспособность ПТУ на
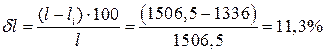 .
.
Эффективная мощность ПТУ:
 ,
,
где 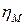 = 0,98 – механический КПД ПТУ и D = 100 кг/с – расход пара через турбину – заданы.
= 0,98 – механический КПД ПТУ и D = 100 кг/с – расход пара через турбину – заданы.
7.Контрольная работа №2
Задача 7.1. Внутри стальной горизонтальной трубы (λст = 20 Вт/м·К) со скоростью W1 течет вода с температурой t1. Снаружи труба охлаждается воздухом (свободная конвекция), температура воздуха – t2. Определить коэффициенты теплоотдачи α1 и α2 соответственно от воды к внутренней стенке трубы и от наружной стенки к воздуху; линейный коэффициент теплопередачи Кl и линейный тепловой поток ql, если внутренний диаметр трубы d1, внешний – d2. Исходные данные взять из табл.7.1.
Указание. Для определения α2 в первом приближении температуру наружной поверхности tw2 принять равной tw1 = 0,5(t1+t2).
Таблица 7.1
Исходные данные к задаче 7.1
| Последняя цифра шифра | t1, ºC | W1, м/с | Предпоследняя цифра шифра | t2, ºC | м | |
| d1 | d2 | |||||
| 0,01 | 0,10 | 0,11 | ||||
| 0,05 | 0,11 | 0,12 | ||||
| 0,10 | 0,12 | 0,13 | ||||
| 0,15 | 0,13 | 0,14 | ||||
| 0,20 | 0,14 | 0,15 | ||||
| 0,25 | 0,15 | 0,16 | ||||
| 0,30 | 0,16 | 0,17 | ||||
| 0,35 | 0,17 | 0,18 | ||||
| 0,40 | 0,18 | 0,19 | ||||
| 0,45 | 0,19 | 0,20 |
Указание. Для определения коэффициентов теплоотдачи физические свойства воды и воздуха взять из табл.7.2, 7.3.
Таблица 7.2
Физические свойства воздуха при нормальном давлении [8]
и теплоемкость золы [9]
| t, ºC | Срm, кДж/кг·К | λ, Вт/м·К | ν·106, м2/с | Рr | Сз, кДж/кг·К |
| 1,003 | 0,0244 | 13,28 | 0,707 | - | |
| 1,003 | 0,0259 | 15,06 | 0,703 | - | |
| 1,003 | 0,0276 | 16,96 | 0,699 | - | |
| 1,004 | 0,0290 | 18,97 | 0,696 | - | |
| 1,004 | 0,0305 | 21,09 | 0,692 | - | |
| 1,005 | 0,0321 | 23,13 | 0,688 | 0,810 | |
| 1,006 | 0,0334 | 25,45 | 0,686 | - | |
| 1,007 | 0,0349 | 27,80 | 0,684 | - | |
| 1,008 | 0,0364 | 30,09 | 0,682 | - | |
| 1,009 | 0,0378 | 32,49 | 0,681 | - | |
| 1,010 | 0,0393 | 34,85 | 0,680 | 0,845 | |
| 1,014 | 0,0427 | 40,61 | 0,677 | - | |
| 1,018 | 0,0460 | 48,33 | 0,674 | 0,880 | |
| 1,022 | 0,0491 | 55,46 | 0,676 | - | |
| 1,027 | 0,0521 | 63,09 | 0,678 | 0,900 | |
| 1,038 | 0,0574 | 79,38 | 0,687 | 0,916 | |
| 1,049 | 0,0622 | 96,89 | 0,699 | 0,935 | |
| 1,060 | 0,0671 | 115,4 | 0,706 | 0,947 | |
| 1,069 | 0,0718 | 134,8 | 0,713 | 0,960 | |
| 1,080 | 0,0763 | 155,1 | 0,717 | 0,971 | |
| 1,090 | 0,0807 | 177,1 | 0,719 | 0,984 | |
| 1,099 | 0,0850 | 199,3 | 0,722 | 0,996 | |
| 1,107 | 0,0915 | 233,7 | 0,724 | 1,005 |
Таблица 7.3
Физические свойства воды на линии насыщения [8]
| t, ºC | ρ, кг/ м3 | Ср, кДж/кг·К | λ, Вт/м·К | ν·106, м2/с | β·104, 1/К | Рr |
| 999,9 | 4,212 | 0,551 | 1,789 | -0,63 | 13,67 | |
| 998,2 | 4,183 | 0,599 | 1,006 | +1,82 | 7,02 | |
| 992,2 | 4,174 | 0,635 | 0,659 | 3,87 | 4,31 | |
| 983,2 | 4,179 | 0,659 | 0,478 | 5,11 | 2,98 | |
| 971,8 | 4,195 | 0,674 | 0,365 | 6,32 | 2,21 | |
| 958,4 | 4,220 | 0,683 | 0,295 | 7,52 | 1,75 | |
| 943,1 | 4,250 | 0,686 | 0,252 | 8,64 | 1,47 | |
| 926,1 | 4,287 | 0,685 | 0,217 | 9,72 | 1,26 | |
| 907,4 | 4,346 | 0,683 | 0,191 | 10,7 | 1,10 | |
| 886,9 | 4,417 | 0,674 | 0,173 | 11,9 | 1,00 | |
| 863,0 | 4,505 | 0,663 | 0,158 | 13,3 | 0,93 | |
| 840,3 | 4,614 | 0,645 | 0,149 | 14,8 | 0,89 | |
| 813,6 | 4,756 | 0,628 | 0,141 | 16,8 | 0,87 | |
| 784,0 | 4,949 | 0,605 | 0,135 | 19,7 | 0,87 | |
| 750,7 | 5,230 | 0,574 | 0,131 | 23,7 | 0,90 | |
| 712,5 | 5,736 | 0,540 | 0,128 | 29,2 | 0,97 | |
| 667,1 | 6,574 | 0,506 | 0,128 | 38,2 | 1,11 | |
| 610,1 | 8,165 | 0,457 | 0,127 | 53,4 | 1,39 | |
| 528,0 | 13,98 | 0,395 | 0,126 | 2,35 |
РЕШЕНИЕ (вариант 99).
Для вынужденной конвекции воды в трубе определяется режим движения по числу Рейнольдса:
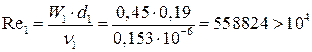 ,
,
то-есть режим движения турбулентный.
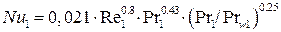 (7.1)
(7.1)
При ламинарном режиме (Re1<2300) уравнение подобия конвективной теплоотдачи имеет вид:
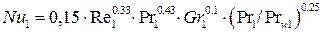 (7.2)
(7.2)
и при переходном режиме (Re1 = 2300…104):
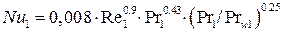 (7.3)
(7.3)
Здесь 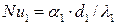 - число Нуссельта:
- число Нуссельта:
 - число Грасгофа;
- число Грасгофа;
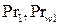 - числа Прандтля воды соответственно при температуре воды t1 и температуре внутренней стенки трубы tw1 , которая в первом приближении принимается равной tw1 = tw2 = 0.5(t1+t2) = 110ºC (Prw1 = 1.6);
- числа Прандтля воды соответственно при температуре воды t1 и температуре внутренней стенки трубы tw1 , которая в первом приближении принимается равной tw1 = tw2 = 0.5(t1+t2) = 110ºC (Prw1 = 1.6);
ν1 = 0,153 ·10-6 м2/с – коэффициент кинематической вязкости воды находится по табл.7.3 при t1 = 210ºC;
λ1 = 0,655 Вт/м·К – коэффициент теплопроводности воды;
g = 9,81м/ с2 – ускорение свободного падения;
β1 = 14,1·10-4 1/К – коэффициент объемного расширения воды,
итак, по уравнению (7.1) для турбулентного режима:
 .
.
Коэффициент конвективной теплоотдачи от воды:
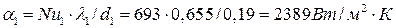 .
.
Число Грасгофа для воздуха:
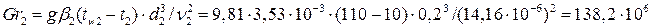 ,
,
где для воздуха  .
.
Коэффициент свободно-конвективной теплоотдачи к воздуху определяется из уравнения подобия:
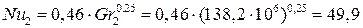 ,
,
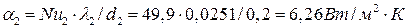 ,
,
где  - коэффициент теплопроводности воздуха при t2 = 10ºC по табл.7.2;
- коэффициент теплопроводности воздуха при t2 = 10ºC по табл.7.2;
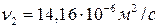 - коэффициент кинематической вязкости воздуха.
- коэффициент кинематической вязкости воздуха.
Линейный коэффициент теплопередачи:
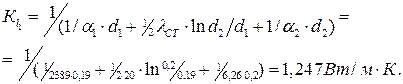
Линейный тепловой поток:
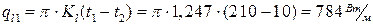 .
.
Температура внутренней поверхности трубы:
 .
.
Температура наружной поверхности трубы:
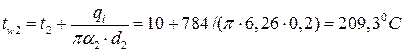 .
.
Второе приближение:
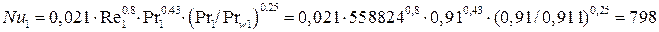 ;
;
 ;
;
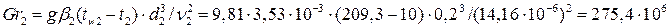 ;
;
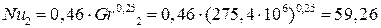 ;
;
 ;
;
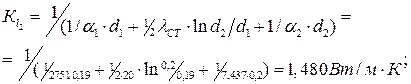
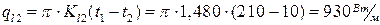 ;
;
 .
.
Расхождения между вторым и первым приближениями велико, следовательно, необходимо третье приближение.
Третье приближение.
 ;
;
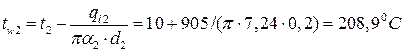 .
.
Так как по сравнению со вторым приближением tw1 изменилась всего на 0,1К, то можно принять Nu1 = 59.3 и α1 = 2751 Вт/м2·К по второму приближению;
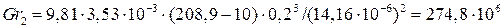 ;
;
 ;
;
 ;
;
 ;
;
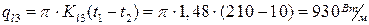 ;
;
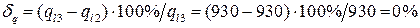 .
.
Это означает, что расчет в третьем приближении точный. Задача решена.
Задача 7.2. Определить поверхность нагрева рекуперативного газовоздушного теплообменника при прямоточной и противоточной схемах движения теплоносителей, если массовый расход нагреваемого воздуха m2, средний коэффициент теплопередачи от газов к воздуху К, начальные и конечные температуры газов и воздуха соответственно: 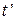 1 и
1 и  1,
1, 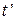 2 и
2 и  2. Исходные данные взять из табл.7.4.
2. Исходные данные взять из табл.7.4.
Изобразить графики изменения температур теплоносителей для обоих случаев.
Таблица 7.4
Исходные данные к задаче 7.2
| Последняя цифра шифра | m2, кг/с | К, Вт/м2·К | Предпоследняя цифра шифра | 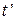 1,
ºC 1,
ºC
|  1,
ºC 1,
ºC
| 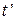 2,
ºC 2,
ºC
|  2,
ºC 2,
ºC
|
РЕШЕНИЕ (вариант 99).
 Рис. 7.2. Противоток.
Рис. 7.2. Противоток.
|
Графики изменения температур теплоносителей приведены на рис.7.1 и 7.2.
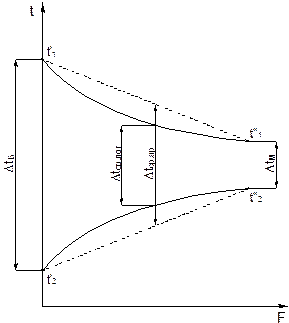 Рис. 7.1. Прямоток.
Рис. 7.1. Прямоток.
|
Тепловой поток, воспринятый нагреваемым воздухом:
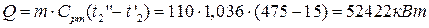 ,
,
где средняя, массовая, изобарная теплоемкость воздуха
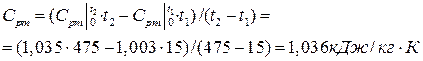 .
.
Здесь средние теплоемкости  взяты из табл.7.2 для воздуха.
взяты из табл.7.2 для воздуха.
Большая и меньшая разности температур между теплоносителями для прямотока:
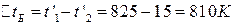 ;
;
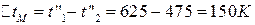 ;
;
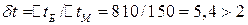 , поэтому средняя разность температур между теплоносителями определяется как средне-логарифмическая:
, поэтому средняя разность температур между теплоносителями определяется как средне-логарифмическая:
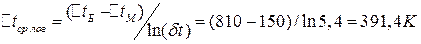 .
.
Необходимая поверхность нагрева прямоточного теплообменника:
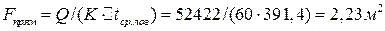 .
.
То же самое для противотока:
 ;
;
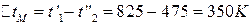 ;
;
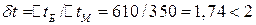 ;
;
то-есть среднюю разность температур между теплоносителями с достаточной точностью можно посчитать, как средне-арифметическую:
 .
.
Необходимая поверхность нагрева противоточного теплообменника:
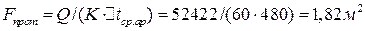 .
.
Среднюю разность температур называют “движущей силой” теплопередачи, при противотоке она больше ( 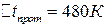 ,
, 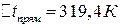 ), поэтому при одинаковых условиях противоточный теплообменник компактнее (Fпрот = 1,82 м2 )<(Fпрям = 2,23 м2 ), требует для своего изготовления меньших затрат материалов (конструктивный расчет).
), поэтому при одинаковых условиях противоточный теплообменник компактнее (Fпрот = 1,82 м2 )<(Fпрям = 2,23 м2 ), требует для своего изготовления меньших затрат материалов (конструктивный расчет).
Если же имеется готовый теплообменник, то при одинаковых условиях получится Qпрот>Qпрям (поверочный расчет) – из-за более высокой “движущей силы” при противотоке. Кроме того, как видно из рис.7.2, при противотоке можно нагреть холодный теплоноситель до температуры  2>
2>  , что невозможно в принципе при прямотоке (см. рис. 7.1).
, что невозможно в принципе при прямотоке (см. рис. 7.1).
ЗАДАЧА 7.3. Задано топливо и паропроизводительность котлоагрегата D. Определить состав топлива по рабочей массе и его низшую теплоту сгорания, способ сжигания топлива, тип топки, значение коэффициента избытка воздуха в топке αТ и в уходящих из топки газах αух по величине присоса воздуха по газовому тракту ∆α; найти теоретически необхо
Дата добавления: 2015-04-16; просмотров: 308; Мы поможем в написании вашей работы!; Нарушение авторских прав |