Законы Кирхгофа. Задача анализа электрической цепи формируется следующем образом.

Задача анализа электрической цепи формируется следующем образом.

Заданы схемы электрической цепи со значениями всех элементов ,а также напряжения и токи источников, действующих в цепи. Требуется найти токи в ветвях и напряжения на элементах цепи .Для определения искомых токов и напряжений необходимо составить уравнения цепи ,которые определяются только геометрической конфигурацией и способами соединения элементов цепи .Эти уравнения составляются на основе двух законов Кирхгофа ,которые связывают токи ветвей ,сходящих в узлах ,и напряжения элементов, входящих в контуры.

Первый закон Кирхгофа: алгебраическая сумма токов в узле равна 0.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на сопротивлении в замкнутом контуре равна алгебраической сумме ЭДС.

Проверка: 1. По узлам, 2. метод баланса мощности (фактически закон сохранения энергии).

1. I=0.

2. Pисточ= Рпотр.

Метод контурных токов.

Методом контурных токов дает возможность упростить расчёт электрических цепей по сравнению методом Кирхгофа за счёт уменьшения числа уравнений ,которые приходится решать совместно. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурные токи ,замыкающиеся на контурах .

рис.1.22

На рис .1.22 в виде примера показаны двухконтурная цепь ,В которой I₁₁ и I₂₂ – контурные токи. Токи в сопротивлениях r₁ и r₂ равны соответствующим контурным токам; ток в сопротивлении r₃ является общим для обоих контуров, равен разности контурных токов I₁₁ и I₂₂ так как эти токи направлены в ветви r₃ встречно.

Число уравнений ,записываемых для контурных токов по второму закону Кирхгофа ,равно числу независимых контуров ,то есть для электрической схемы с числом узлов q и числом ветвей p задача нахождения контурных токов ведется к решению системы p-q+1 уравнений .Так ,в схеме рис.1.22 q=2 p=3 ; cледовательно , число уравнений равно 3-2+1=2(число уравнений независимых контуров).Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падения напряжения от заданного контурного тока в сопротивлениях ,входящих в контур ,берется со знаком плюс .Падение напряжения от тока смежного контура в общем сопротивлении берется с знаком минус ,если контурные токи в этом сопротивлении направлены встречно, как это ,например, имеет место в схеме рис.1.22 где направление обоих контурных токов выбрано по ходу часовой стрелки.

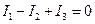
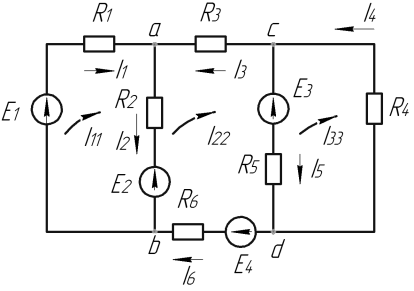
I11, I22, I33 – контурные токи.

I11=I1;

I22=-I2;

I33=-I4.

Rnn – сумма всех сопротивлений в сумма всех сопротивлений в n-ом контуре.

R12 – сопротивление между 1-м и 2-м контуром со знаком «-».

Enn – сумма всех ЭДС в n-м контуре.