
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Трехфазный источник и трехфазная линейная цепь
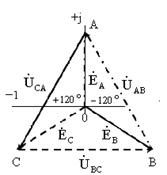
Под симметричной трехфазной системой ЭДС понимается совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе между собой на угол 120°. Графики мгновенных значений ЭДС представлены на рис. 8.1, а, векторная диаграмма – на рис. 8.1, б.
 а
а
|  б
б
|
| Рис. 8.1. Временная и векторная диаграмма трехфазной системы |
Одну из ЭДС обозначают  , отстающую от этой ЭДС по фазе на угол –120° –
, отстающую от этой ЭДС по фазе на угол –120° –  а опережающую на угол +120° –
а опережающую на угол +120° –  Как видно из векторной диаграммы,
Как видно из векторной диаграммы, 
 и
и  где
где  напряжения между началом и концом фазы генератора называют фазным напряжением. Напряжения между фазами:
напряжения между началом и концом фазы генератора называют фазным напряжением. Напряжения между фазами:


 (8.1)
(8.1)
где  – напряжение между двумя любыми фазами генератора называют линейнымнапряжением.
– напряжение между двумя любыми фазами генератора называют линейнымнапряжением.
Из векторной диаграммы можно установить, что 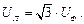
Основным свойством симметричной трехфазной системы ЭДС является:
 ,
,

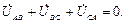 (8.2)
(8.2)
Чередованием фаз называется последовательность прохождения ЭДС через одинаковое значение, например нулевое или другое. Если фазные ЭДС проходят через нулевое значение в последовательности 
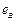 и
и 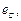 то последовательность чередования фраз называют прямой.
то последовательность чередования фраз называют прямой.
Трехфазной цепью называется цепь, содержащая трехфазную систему ЭДС, трехфазную нагрузку и соединительные проводники (рис. 8.2).

|
| Рис. 8.2. Схема подключения трехфазной системы ЭДС |
Проводники, соединяющие начала фаз генератора и нагрузки, называются линейными. Напряжение между нулевыми точками генератора и нагрузки называют напряжением смещения нейтрали 
Фазойтрехфазной цепи также называют однофазную цепь, входящую в состав трехфазной цепи, в которой протекает одинаковый ток.
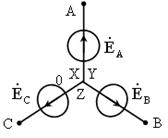
Трехфазная система ЭДС и трехфазная нагрузка могут иметь соединение звездой или треугольником (рис. 8.3, а, б и 8.4, а, б). При соединении обмоток фаз генератора звездой концы фаз X, Y и Z соединяют в одну точку, называемую нулевой или нейтральной. При соединении обмоток фаз генератора треугольником конец одной фазы соединяют с началом другой (рис. 8.3).
Если ЭДС или сопротивления в звезде или треугольнике имеют одинаковое значение, то они называются симметричными, в противном случае – несимметричными. Если сопротивления в нагрузке имеют одинаковый характер (все три сопротивления активные, только индуктивные или емкостные), то такая нагрузка называется однородной, в противном случае – неоднородной.
Токи в фазах называются фазными токами, токи в линиях – линейными.
 а
а
|  б
б
|
| Рис. 8.3. Соединение трехфазной системы ЭДС | |
 а
а
|  б
б
|
| Рис. 8.4. Соединение трехфазной нагрузки |
8.1.2. Соединение источника и нагрузки звезда – звезда
На рис. 8.5 показана трехфазная цепь при соединении источника и нагрузки звезда – звезда. Определим суммарные сопротивления в линиях:


 (8.3)
(8.3)
При наличии нулевого провода напряжение смещения нейтрали рассчитаем методом двух узлов:
 (8.4)
(8.4)
Токи в линиях и нейтрали определим по закону Ома:
 ,
,  ,
, 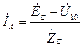 и
и  . (8.5)
. (8.5)
При разомкнутом ключе нулевой провод отсутствует  и
и 

|
| Рис. 8.5. Соединение звезда – звезда без нулевого провода |
При замкнутом ключе и сопротивлении нулевого провода  , смещение
, смещение  и ток в нейтрали:
и ток в нейтрали:
 (8.6)
(8.6)
токи в линиях:

 и
и  (8.7)
(8.7)
При разомкнутом или замкнутом ключе и симметричной нагрузке 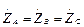 смещение
смещение  ток в нейтрали и
ток в нейтрали и  а токи в линиях можно определить по (8.7).
а токи в линиях можно определить по (8.7).
На рис. 8.6 изображены векторные диаграммы напряжений и токов, соответствующие схеме рис. 8.5 для замкнутого положения ключа.
 а
а
|  б
б
|
| Рис. 8.7. Векторные диаграммы подключения звезда-звезда |
8.1.3. Соединение источника и нагрузки звезда – треугольник
На рис. 8.7 показана трехфазная цепь при соединении источника и нагрузки звезда – треугольник. Определим суммарные сопротивления в линиях.
Токи в линейных проводах можно определить, преобразовав треугольник сопротивлений в звезду и используя соотношения (8.3)–(8.5).
 ,
,
 ,
,
 ,
,
 (8.8)
(8.8)

| |
Рис. 8.7. Подключение звезда – треугольник
Токи в нагрузке найдем через напряжения  , ,  и и 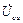 на сопротивлениях нагрузки: на сопротивлениях нагрузки:

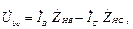
 (8.9) (8.9)
 ; ;  ; ;  (8.10)
В большинстве случаев сопротивлениями линий (8.10)
В большинстве случаев сопротивлениями линий   и и  можно пренебречь, тогда напряжения на нагрузке будут равны линейным напряжениям источника: можно пренебречь, тогда напряжения на нагрузке будут равны линейным напряжениям источника:
 ; ;  ; ;  Токи в нагрузке определим по (8.10), а токи в линиях – по первому закону Кирхгофа:
Токи в нагрузке определим по (8.10), а токи в линиях – по первому закону Кирхгофа:
 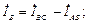  (8.11)
Совмещенные векторные диаграммы напряжений и токов приведены на рис. 8.8. (8.11)
Совмещенные векторные диаграммы напряжений и токов приведены на рис. 8.8.
| |

| |
| Рис. 8.8. Векторные диаграммы подключения звезда – треугольник |
Дата добавления: 2015-04-16; просмотров: 271; Мы поможем в написании вашей работы!; Нарушение авторских прав |