
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Необходимые приборы и оборудование
Стенд с:
1. Источником напряжения.
2. Катушкой индуктивности.
3. Батареей конденсаторов.
4. Резистором.
5. Амперметром.
6. Вольтметром.
ОБЩИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
При изучении данной работы необходимо ознакомиться с теоретическими сведениями, изложенными в работе №3.
При расчете разветвленных цепей переменного тока наиболее часто используют метод проводимостей, при котором сопротивление каждой ветви заменяют на ее проводимость. При таком подходе выражение для определения полной проводимости цепи с параллельным соединением проводников имеет такой же простой вид, как и выражение для определения полного сопротивления цепи при последовательном соединении элементов.
Рассмотрим некоторые примеры разветвленных цепей переменного тока:
Параллельное соединение идеализированных R-, L-, C- элементов.
Схема параллельного соединения указана на рис. 28:

Рис. 28. Параллельное сопротивление R-, L-, C- элементов
Проводимости каждой ветви:
g=1/R – активная проводимость ветви,
bL=1/XL – реактивная индуктивная проводимость ветви,
bC=1/XC – реактивная емкостная проводимость ветви, где
XL=wL, XC=1/(wC) – сопротивления идеальной индуктивности и емкости соответственно. Тогда полная проводимость цепи:
 .
.
Согласно закону Ома, токи протекающие по цепи:
IR=gU, IL=bLU, IC=bCU,
 ,
,
где I0 – ток в общем проводе.
Построим векторную диаграмму для цепи, изображенной на рис. 28.
Построение следует начинать с вектора напряжения U, т.к. оно общее для всех элементов цепи. Вектор тока IR совпадает по фазе с вектором напряжения U. Ток, протекающий в идеальной катушке индуктивности, отстает от приложенного к ней напряжения на 90о. Ток, протекающий через идеальный конденсатор, опережает на 90о приложенный к нему вектор напряжения.
На основании первого закона Кирхгофа векторная сумма токов всех ветвей есть ток, протекающий в общем проводе. Тогда векторная диаграмма (в предположении, что bL<bC) примет вид (рис. 29):
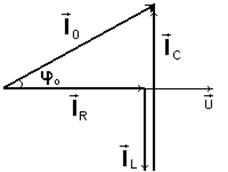
Рис.29. Векторная диаграмма идеализированных R-, L-, C- элементов
Явление, при котором векторы тока IL и IC по модулю равны друг другу, т.е. их векторная сумма равна нулю, называют резонансом токов. При этом общий ток в цепи Iо минимален и совпадает по фазе с вектором напряжения (jо=0).
Согласно условию резонанса можно подобрать такие элементы L и С, что ток в общем проводе Iо будет много меньше чем на каждом из элементов L и C (Io<<IL, Io<<IC).
Параллельное соединение реальных L-, C- элементов.
Реальные конденсаторы и катушки индуктивности помимо реактивного сопротивления обладают еще и активным сопротивлением. Их можно представить как последовательное соединение идеальных L и C элементов и внутреннего активного сопротивления (рис.30):

Рис. 30. Параллельное соединение реальных L- и C- элементов с внутренним сопротивлением r1 и r2.
Тогда токи в ветвях:
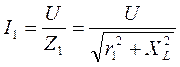 ,
, 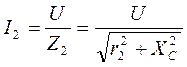 ,
,
где Z1, Z2 – полные сопротивления ветвей. Причем сдвиги фаз между напряжением U и токами I1, I2:
 ,
, 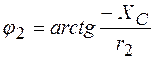 .
.
Построим векторную диаграмму электрической цепи, изображенной на рис. 30:
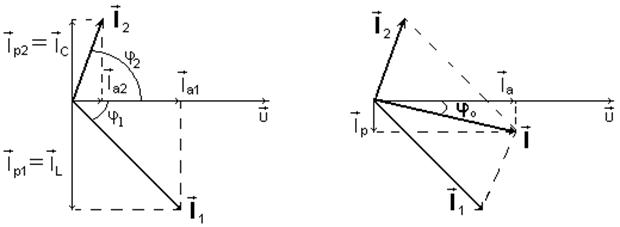
Рис. 31. Векторная диаграмма электрической схемы, изображенной на рис.30.
Токи I1, I2 можно разложить на составляющие: активную, совпадающую по фазе с напряжением и реактивную, отстоящую от напряжения на угол 90о.
Общий ток I найдем путем сложения векторов I1, I2 по правилу параллелограмма. Его активная и реактивная составляющие:
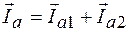 ,
, 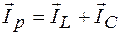
Таким образом, длина вектора 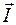 :
:
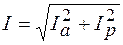 ,
,
а сдвиг фаз между током и напряжением определяется через tg:
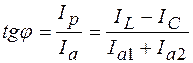
Так в неразветвленной части цепи (ток в общем проводе) может отставать от напряжения (при IL>IC), опережать его (при IL<IC) и, наконец, совпадать по фазе с напряжением (при IL=IC). В последнем случае возникает резонанс токов, при котором
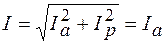 ,
, 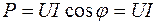 .
.
Коэффициент мощности.
Связь полной и реактивной мощности выражается формулой:
 ,
,
откуда
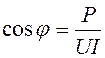 - коэффициент мощности.
- коэффициент мощности.
Таким образом, коэффициент мощности генератора (электростанции) зависит от потребителя. Директивными указаниями его значение установлено 0,9 – 0,92, к которому должно стремиться каждое промышленное предприятие. Большинство приемников промышленных предприятий составляют электродвигатели и другие электромагнитные механизмы. При холостом ходе двигателя его  , а при номинальной нагрузке
, а при номинальной нагрузке  . Для повышения коэффициента мощности можно:
. Для повышения коэффициента мощности можно:
1. Увеличить нагрузку двигателей и поддерживать ее близкой к номинальной;
2. Заменить слабо загруженные двигатели двигателями меньшей мощности, с тем чтобы они работали с номинальной нагрузкой;
3. Установить синхронный электродвигатель, вызывающий в цепи опережающий реактивный ток;
4. Включить параллельно двигателю батарею конденсаторов.
Если параллельно приемнику (электродвигателю), потребляющему ток I1 и работающему с коэффициентом мощности 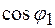 подключить батарею конденсаторов, то в цепи возникает емкостной ток IC, опережающий напряжение на 90о (при идеальном конденсаторе). Ток I в проводах линии, равный сумме токов I1, IC будет меньше тока I1 и будет сдвинут от напряжения на угол
подключить батарею конденсаторов, то в цепи возникает емкостной ток IC, опережающий напряжение на 90о (при идеальном конденсаторе). Ток I в проводах линии, равный сумме токов I1, IC будет меньше тока I1 и будет сдвинут от напряжения на угол  (см. рис. 32).
(см. рис. 32).

Рис.32. Векторная диаграмма с параллельным подключением конденсатора к электродвигателю с индуктивной нагрузкой
Таким образом, коэффициент мощности всей установки увеличивается вследствие частичной (или полной) компенсации реактивной составляющей тока двигателя током конденсатора.
Рассчитаем емкость конденсаторов, необходимую для повышения коэффициента мощности до требуемого значения:
Тангенс угла сдвига для двигателя
 ,
,
откуда
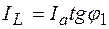 .
.
Результирующий реактивный ток установки
 .
.
Тогда тангенс угла сдвига установки:
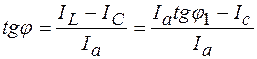 ,
,
откуда
 .
.
Учитывая, что  и
и 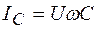 , получим:
, получим:
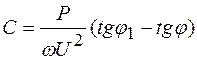 .
.
В большинстве случаев компенсация реактивного тока выполняется не полностью, а удовлетворяется повышением  до значения 0,95. Дальнейшее повышение
до значения 0,95. Дальнейшее повышение  экономически не оправдывается из-за стоимости дополнительной батареи конденсаторов значительной емкости.
экономически не оправдывается из-за стоимости дополнительной батареи конденсаторов значительной емкости.
Повышение  означает значительную экономию электрической энергии и является важной технико-экономической проблемой.
означает значительную экономию электрической энергии и является важной технико-экономической проблемой.
Дата добавления: 2015-04-16; просмотров: 302; Мы поможем в написании вашей работы!; Нарушение авторских прав |