Применение законов Кирхгофа для расчета сложных цепей

Для каждой сложной цепи, пользуясь законами Кирхгофа, можно составить строго определенное число независимых друг от друга уравнений. Как будет показано ниже, это число всегда равно числу неизвестных токов в цепи.
Число уравнений находится в зависимости от числа ветвей (n) и числа узлов (k). Любая ветвь цепи характеризуется величиной э. д. с. (Е) действующей в ней, сопротивлением (R) и величиной тока (I).
Если в данной ветви действуют несколько э. д. с. и имеется несколько сопротивлений, то она характеризуется алгебраической суммой всех э. д. с. и суммой всех сопротивлений, т.е. опять-таки определенной (одной) э. д. с. и определенным (одним) сопротивлением.
Следовательно, сложная цепь, имеющая n ветвей, будет характеризоватьсяn-э. д. с., n-сопротивлениямии n-токами.

Используя первый закон Кирхгофа, можно составить (k-1) уравнений, связывающих между собой величины токов в ветвях. Таким образом, число уравнений на одно меньше, чем число всех узлов цепи. Это объясняется тем, что все токи, входящие в уравнение для узла k, уже вошли в предыдущие уравнения. На схеме в узле А сходятся токиI₁, I₂, I₃; в узле В —I₂, I₃, I₄, I₅; в узле С — I₄, I₅, I₁.

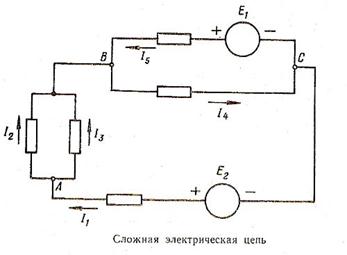
Уравнения первого закона Кирхгофа для узлов А и В являются независимыми. В то же время уравнение для узла С. Дает нам зависимость, которая может быть получена на основании уравнений, составленных для первых двух узлов.
В самом деле, на основании первого закона Кирхгофа получим:

— для узла А
I₁-I₂-I₃=0; (1)
— для узла В
I₂+I₃+I₅-I₄=0; (2)
— для узла С
I₄-I₁-I₅=0. (3)

Но последнее уравнение не является независимым, так как может быть получено на основании двух первых.
Действительно, складывая (1) и (2), получим

I₁-I₄+I₅=0,

а умножив обе части равенства на -1, будем иметь

I₄-I₁-I₅=0

Определим теперь число уравнений, которое можно составить, используя второй закон Кирхгофа. Для того чтобы эти уравнения были независимы друг от друга, достаточно чтобы контуры, для которых они пишутся, отличались хотя бы одной ветвью, входящей в их состав.
Математически доказано, что число независимых уравнений m, которое можно составить для любой сложной цепи по второму закону Кирхгофа будет равно

m = n-k + 1,

где m —число независимых уравнений, составленных по второму закону Кирхгофа;
n— число ветвей;
к — число узлов.
При выборе контуров стараются по возможности подобрать такие, которые содержат меньшее число ветвей и э. д. с.
Общее число уравнений, составляемых по первому и второму законам Кирхгофа для сложной цепи, состоящей из ветвей и узлов, будет равно числу ветвей.
Складывая число уравнений, составленных на основании первого закона Кирхгофа (k—1), с числом уравнений, составленных на основании второго закона Кирхгофа (m), получим

k — 1 + m = k— 1 + n — k + 1 = n.

Итак, если задана цепь из n ветвей и известны все э. д. с. и сопротивления, всегда можно составитьn уравнений по числу неизвестных токов в ветвях.
Для решения задачи на расчет сложной цепи необходимо:

1. По схеме цепи установить числа n и k, для чего пронумеровать все ветви и узлы данной сложной цепи
2. Показать на схеме направления (предположительные) токов в каждой из ветвей.

3. Определить, для каких (k—1) узлов нужно составить уравнение первого закона Кирхгофа и для каких контуров нужно составить уравнение второго закона Кирхгофа.

4. Для выбранных узловых точек схемы составить (k — 1) уравнений по первому закону Кирхгофа:

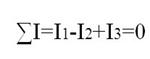
Суммирование токов производится обязательно с учетом знака.
5. Для выбранных замкнутых контуров составить m уравнений по второму закону Кирхгофа:

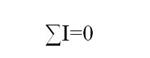
При составлении этих уравнений э. д. с. суммируются с учетом знака, а падения напряжения берутся со знаком плюс, если направление тока совпадает с направлением обхода контура, и наоборот.
6. Решить систему полученных уравнений, в результате чего определяются величины токов во всех ветвях цепи. Если при решении та или иная величина тока получается со знаком минус, то это значит, что фактическое направление тока в данной ветви обратно тому, которое было принято предварительно.
Для закрепления рассматриваемого порядка расчета сложной цепи с использованием законов Кирхгофа решим пример.

I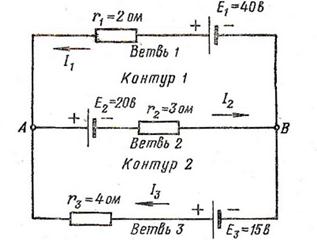

Пример. Дана сложная цепь, изображенная на рисунке. Зная Е₁, Е₂, Е₃, r₁r₂и r₃, необходимо определить токи в ветвях I₁, I₂и I₃.

Решение.
1. Анализируя данную схему, устанавливаем, что в ней число ветвей n равно трем, а число узлов k равно двум.
2. Обозначим направление токов в ветвях. Это не значит, что они будут именно такими, как мы предположили. Истинное направление токов определится в ходе решения задачи.
3. Уравнения первого закона Кирхгофа необходимо составить для
(k-1) узлов, или2-1= 1.
Количество уравнений второго закона Кирхгофа, которое надо составить для решения задачи будет равно

m = n-(k- 1) = 3 - (2 - 1) = 3 - 1=2.

4. Составим одно уравнение по первому закону Кирхгофа для узла А:

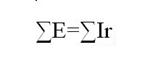
5. Приняв направление обхода контуров против часовой стрелки, составим m-2 уравнений для замкнутых контуров по второму закону Кирхгофа:
— для контура № 1:

Е₁– Е₂= I₁r₁+ I₂r₂ (5)

— для контура № 2:

Е₂-E₃= - I₂r₂- I_Зг₃. (6)

6. Решаем систему из трех уравнений.
Из уравнения, составленного по первому закону Кирхгофа (4),
имеем
I₁=I₂-I₃

Подставим полученное значение тока в уравнение (5)

E₁-E₂=(I₂-I₃) r₁+I₂r₂

Подставим числовые значения и уравнения (5) и (6).

40 -20 = (I₂-I₃)*2 +I₂*3; (7)
20-15=-I₂*3-I₃*4. (8)

Упростим эти уравнения и решим их методом подстановки:

20=5*I₂-2I₃;
5=-3*I₂-4I₃

Умножим уравнение (7) на 2 и вычтем из полученного результата уравнение (8)

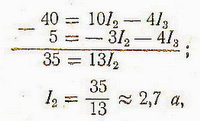
далее, подставляя значение I₂ в уравнение (8), получим

5= -3*2,7-4I₃; 4I₃= -13,1;
I₃= -13,1/4=-3,3A.

Теперь из уравнения (6) находим ток I₁:

I₁=I₂-I₃=2,7-(-3,3)=6A.

В результате решения токи I₂ и I₁ имеют положительное, а ток I₃ —
отрицательное значение, следовательно, фактическое направление токовI₂
иI₁ совпадает с принятым, а тока I₃— обратно принятому в начале решения задачи.