Тангенциальная составляющая ускорения 13 страница. § 68. Давление под искривленной поверхностью жидкости

§ 68. Давление под искривленной поверхностью жидкости

Если поверхность жидкости не плоская, а искривленная, то она оказывает на жидкость избыточное (добавочное) давление. Это давление, обусловленное силами поверхност­ного натяжения, для выпуклой поверхности положительно, а для вогнутой поверх­ности — отрицательно.

Для расчета избыточного давления предположим, что свободная поверхность жидкости имеет форму сферы радиуса R, от которой мысленно отсечен шаровой сегмент, опирающийся на окружность радиуса r=Rsina (рис. 100). На каждый бес­конечно малый элемент длины Dl этого контура действует сила поверхностного натяжения DF = s Dl, касательная к поверхности сферы. Разложив DF на два компонента (DF₁ и DF₂), видим, что геометрическая сумма сил DF₂ равна нулю, так как эти силы на противоположных сторонах контура направлены в обратные стороны и взаимно уравновешиваются. Поэтому равнодействующая сил поверхностного натяжения, дей­ствующих на вырезанный сегмент, направлена перпендикулярно плоскости сечения внутрь жидкости и равна алгебраической сумме составляющих DF₁:

Разделив эту силу на площадь основания сегмента pr², вычислим избыточное давление на жидкость, создаваемое силами поверхностного натяжения и обусловленное кривиз­ной поверхности:

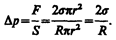(68.1)

Если поверхность жидкости вогнутая, то можно доказать, что результирующая сила поверхностного натяжения направлена из жидкости и равна

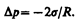(68.2)

Следовательно, давление внутри жидкости под вогнутой поверхностью меньше, чем в газе, на величину Dp.

Формулы (68.1) и (68.2) являются частным случаем формулы Лапласа,* опре­деляющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:

(68.3)

где R₁ и R₂ — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости в дайной точке. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости.

*П. Лаплас (1749—1827) — французский ученый.

Для сферической искривленной поверхности (R₁=R₂=R) выражение (68.3) перехо­дит в (68.1), для цилиндрической (R₁=R и R₂=¥) — избыточное давление

В случае плоской поверхности (R₁=R₂=¥) силы поверхностного натяжения избыточного давления не создают.

§ 69. Капиллярные явления

Если поместить узкую трубку(капилляр) одним концом в жидкость, налитую в широ­кий сосуд, то вследствие смачивания или несмачивания жидкостью стенок капилляра кривизна поверхности жидкости в капилляре становится значительной. Если жидкость смачивает материал трубки, то внутри ее поверхность жидкости —мениск — имеет вогнутую форму, если не смачивает — выпуклую (рис. 101).

Под вогнутой поверхностью жидкости появится отрицательное избыточное давле­ние, определяемое по формуле (68.2). Наличие этого давления приводит к тому, что жидкость в капилляре поднимается, таккак под плоской поверхностью жидкости в широком сосуде избыточного давления нет. Если же жидкость не смачивает стенки капилляра, то положительное избыточное давление приведет к опусканию жидкости в капилляре. Явление изменения высоты уровня жидкости в капиллярах называется капиллярностью. Жидкость в капилляре поднимается или опускается на такую высоту h, при которой давление столба жидкости (гидростатическое давление) rgh уравновеши­вается избыточным давлением Dp, т. е.

где r — плотность жидкости, g — ускорение свободного падения.

Если r — радиус капилляра, q — краевой угол, то из рис. 101 следует, что (2s cosq)/r = rgh, откуда

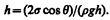(69.1)

В соответствии с тем, что смачивающая жидкость по капилляру поднимается, а несмачивающая—опускается, из формулы (69.1) при q<p/2 (cosq>0) получим положительные значения h, а при q>p/2 (cosq<0) — отрицательные. Из выражения (69.1) видно также, что высота поднятия (опускания) жидкости в капилляре обратно пропорциональна его радиусу. В тонких капиллярах жидкость поднимается достаточно высоко. Так, при полном смачивании (q=0) вода (r =1000 кг/м³, s = 0,073 Н/м) в ка­пилляре диаметром 10мкм поднимается на высоту h »3 м.

Капиллярные явления играют большую роль в природа и технике. Например, влагообмен в почве и в растениях осуществляется за счет поднятия воды по тончайшим капиллярам. На капиллярности основано действие фитилей, впитывание влаги бетоном и т. д.

§ 70. Твердые тела. Моно- и поликристаллы

Твердые тела (кристаллы) характеризуются наличием значительных сил межмолекулярного взаимодействия и сохраняют постоянными не только свой объем, но и форму. Кристаллы имеют правильную геометрическую форму, которая, как показали рент­генографические исследования немецкого физика-теоретика М. Лауэ (1879—1960), яв­ляется результатом упорядоченного расположения частиц (атомов, молекул, ионов), составляющих кристалл. Структура, для которой характерно регулярное расположение частиц с периодической повторяемостью в трех измерениях, называется кристалличес­кой решеткой. Точки, в которых расположены частицы, а точнее — средние равновес­ные положения, около которых частицы совершают колебания, называются узлами кристаллической решетки.

Кристаллические тела можно разделить на две группы: монокристаллы и поли­кристаллы. Монокристаллы — твердые тела, частицы которых образуют единую кри­сталлическую решетку. Кристаллическая структура монокристаллов обнаруживается по их внешней форме. Хотя внешняя форма монокристаллов одного типа может быть различной, но углы между соответствующими гранями у них остаются постоянными. Это закон постоянства углов, сформулированный М. В. Ломоносовым. Он сделал важный вывод, что правильная форма кристаллов связана с закономерным размещени­ем частиц, образующих кристалл. Монокристаллами являются большинство минера­лов. Однако крупные природные монокристаллы встречаются довольно редко (напри­мер, лед, поваренная соль, исландский шпат). В настоящее время многие монокристал­лы выращиваются искусственно. Условия роста крупных монокристаллов (чистый раствор, медленное охлаждение и т. д.) часто не выдерживаются, поэтому большинст­во твердых тел имеет мелкокристаллическую структуру, т. е. состоит из множества беспорядочно ориентированных мелких кристаллических зерен. Такие твердые тела называются поликристаллами (многие горные породы, металлы и сплавы).

Характерной особенностью монокристаллов является их анизотропность, т. е. зави­симость физических свойств — упругих, механических, тепловых, электрических, маг­нитных, оптических — от направления. Анизотропия монокристаллов объясняется тем, что в кристаллической решетке различно число частиц, приходящихся на оди­наковые по длине, но разные по направлению отрезки (рис. 102), т. е. плотность расположения частиц кристаллической решетки по разным направлениям неодинакова, что и приводит к различию свойств кристалла вдоль этих направлений. В поликристаллах анизотропия наблюдается только для отдельных мелких кристалликов, но их различная ориентация приводит к тому, что свойства поликристалла по всем направле­ниям в среднем одинаковы.

.

§ 71. Типы кристаллических твердых тел

Существует два признака для классификации кристаллов: 1) кристаллографический; 2) физический (природа частиц, расположенных в узлах кристаллической решетки, и характер сил взаимодействия между ними).

1. Кристаллографический признак кристаллов. В данном случае важна только про­странственная периодичность в расположении частиц, поэтому можно отвлечься от их внутренней структуры, рассматривая частицы как геометрические точки.

Кристаллическая решетка может обладать различными видами симметрии. Сим­метрия кристаллической решетки — ее свойство совмещаться с собой при некоторых пространственных перемещениях, например параллельных переносах, поворотах, от­ражениях или их комбинациях и т. д. Кристаллической решетке, как доказал русский кристаллограф Е. С. Федоров (1853—1919), присущи 230 комбинаций элементов сим­метрии, или 230 различных пространственных групп.

С переносной симметрией в трехмерном пространстве связывают понятие трехмер­ной периодической структуры — пространственной решетки, или решетки Бравэ, пред­ставление о которой введено французским кристаллографом О. Бравэ (1811—1863). Всякая пространственная решетка может быть составлена повторением в трех различ­ных направлениях одного и того же структурного элемента — элементарной ячейки. Всего существует 14 типов решеток Бравэ, различающихся по виду переносной симмет­рии. Они распределяются по семи кристаллографическим системам, или сингониям, представленным в порядке возрастающей симметрии в табл. 3. Для описания элементарных ячеек пользуются кристаллографическими осями координат, которые проводят параллельно ребрам элементарной ячейки, а начало координат выбирают в левом углу передней грани элементарной ячейки. Элементарная кристаллическая ячейка представ­ляет собой параллелепипед, построенный на ребрах а, b, с с углами a, b и g между ребрами (табл. 3). Величины а, b и с и a, b и g называются параметрами элементарной ячейки и однозначно ее определяют.

2. Физический признак кристаллов. В зависимости от рода частиц, расположенных в узлах кристаллической решетки, и характера сил взаимодействия между ними кри­сталлы разделяются на четыре типа: ионные, атомные, металлические, молекулярные.

Ионные кристаллы. В узлах кристаллической решетки располагаются поочередно ионы противоположного знака. Типичными ионными кристаллами являются большин­ство галоидных соединений щелочных металлов (NaCl, CsCl, КВr и т. д.), а также оксидов различных элементов (MgO, СаО и т. д.). Структуры решеток двух наиболее характерных ионных кристаллов — NaCl (решетка представляет собой две одинаковые гранецентрированные кубические решетки, вложенные друг в друга; в узлах одной из этих решеток находятся ионы Na⁺, в узлах другой — ионы Cl^–) и CsCl (кубическая объемно центрированная решетка — в центре каждой элементарной решетки находит­ся ион) — показаны на рис. 103. Силы взаимодействия между ионами являются в основном электростатическими (кулоновскими).Связь, обусловленная кулоновскими силами притяжения между разноименно заряженными ионами, на­зываетсяионной (илигетерополярной).В ионной решетке нельзя выделить от­дельные молекулы: кристалл представ­ляет собойкак бы одну гигантскую мо­лекулу.

Таблица 3

Атомные кристаллы. В узлах кри­сталлической решетки располагаются нейтральные атомы, удерживающиеся в узлах решеткигомеополярными, или ковалентными, связями квантово-механического происхождения (у соседних атомов обобществлены валентные элек­троны, наименее связанные с атомом). Атомными кристаллами являются ал­маз и графит (два различных состояния углерода), некоторые неорганические со­единения (ZnS, ВеО и т. д.), а также типичные полупроводники — германий Ge и кремний Si. Структура решетки алмаза приведена на рис. 104, где каж­дый атом углерода окружен четырьмя такими же атомами, которые располага­ются на одинаковых расстояниях от него в вершинах тетраэдров.

Валентные связи осуществляются па­рами электронов, движущихся по орби­там, охватывающим оба атома, и носят направленный характер: ковалентные силы направлены от центрального ато­ма к вершинам тетраэдра. В отличие от графита решетка алмаза не содержит плоских слоев, что не позволяет сдви­гать отдельные участки кристалла, по­этому алмаз является прочным соедине­нием.

Металлические кристаллы. В узлах кристаллической решетки располагают­ся положительные ионы металла. При образовании кристаллической решетки валент­ные электроны, сравнительно слабо связанные с атомами, отделяются от атомов и коллективизируются: они уже принадлежат не одному атому, как в случае ионной связи, и не паре соседних атомов, как в случае гомеополярной связи, а всему кристаллу в целом. Таким образом, в металлах между положительными ионами хаотически, подобно молекулам газа, движутся «свободные» электроны, наличие которых обес­печивает хорошую электропроводность металлов. Так как металлическая связь не имеет направленного действия и положительные ионы решетки одинаковы по свойст­вам, то металлы должны иметь симметрию высокого порядка. Действительно, большинство металлов имеют кубическую объемно центрированную (Li, Na, К, Rb, Cs) и кубическую гранецентрированную (Сu, Ag, Pt, Au) решетки. Чаще всего металлы встречаются в виде поликристаллов.

Молекулярные кристаллы. В узлах кристаллической решетки располагаются ней­тральные молекулы вещества, силы взаимодействия между которыми обусловлены незначительным взаимным смещением электронов в электронных оболочках атомов. Эта силы называются ван-дер-ваальсовыми, так как они имеют ту же природу, что и силы притяжения между молекулами, приводящими к отклонению газов от идеаль­ности. Молекулярными кристаллами являются, например, большинство органических соединений (парафин, спирт, резина и т. д.), инертные газы (Ne, Аr, Кr, Хе) и газы СО₂, О₂, N₂ в твердом состоянии, лед, а также кристаллы брома Вr₂, иода I₂. Ван-дер-ваальсовы силы довольно слабые, поэтому молекулярные кристаллы легко деформируются.

В некоторых твердых телах одновременно может осуществляться несколько видов связи. Примером может служить графит (гексагональная решетка). Решетка графита (рис. 105) состоит из ряда параллельных плоскостей, в которых атомы углерода расположены в вершинах правильных шестиугольников. Расстояние между плоскостя­ми более чем в два раза превышает расстояние между атомами шестиугольника. Плоские слои связаны друг с другом ван-дер-ваальсовыми силами. В пределах слоя три валентных электрона каждого атома углерода образуют ковалентную связь с сосед­ними атомами углерода, а четвертый электрон, оставаясь «свободным», коллективизи­руется, но не во всей решетке, как в случае металлов, а в пределах одного слоя. Таким образом, в данном случае осуществляются три вида связи: гомеополярная и метал­лическая — в пределах одного слоя; ван-дер-ваальсова — между слоями. Этим объяс­няется мягкость графита, так как его слон могут скользить друг относительно друга.

Различие в строении кристаллических решеток двух разновидностей углеро­да — графита и алмаза — объясняет различие в их физических свойствах: мягкость графита и твердость алмаза; графит — проводник электричества, алмаз — диэлектрик (нет свободных электронов) и т. д.

Расположение атомов в кристаллах характеризуется такжекоординационным чис­лом — числом ближайших однотипных с данным атомом соседних атомов в кристал­лической решетке или молекул в молекулярных кристаллах. Для модельного изображения кристаллических структур из атомов и ионов пользуются системой плотной упаковки шаров. Рассматривая простейший случай плотной упаковки шаров оди­накового радиуса на плоскости, приходим к двум способам их расположения (рис. 106, а, б). Правая упаковка является более плотной, так как при равном числе шаров площадь ромба со стороной, равной стороне квадрата, меньше площади квадрата. Как видно из рисунка, различие в упаковках сводится к различию ко­ординационных чисел: в левой упаковке координационное число равно 4, в правой — 6, т. е. чем плотнее упаковка, тем больше координационное число.

Рассмотрим, при каких условиях плотная упаковка шаров в пространстве может соответствовать той или иной кристаллической структуре, приводимой ранее. Начнем строить решетку со слоя шаров, представленных на рис. 106, б. Для упрощения дальнейших рассуждений спроецируем центры шаров на плоскость, на которой они лежат, обозначив их белыми кружками (рис. 107). На эту же плоскость спроецируем центры просветов между шарами, которые обозначены на рис. 107 соответственно черными кружками и крестиками. Любой плотноупакованный слой будем называть слоем А, если центры его шаров расположены над серыми кружками, слоем В — если над красными кружками, слоем С — если над крестиками. Над слоем А уложим второй плотноупакованный слой так, чтобы каждый шар этого слоя лежал на трех шарах первого слоя. Это можно сделать двояко: взять в качестве второго слоя либо В, либо С. Третий слой можно опять уложить двояко и т. д. Итак, плотную упаковку можно описать как последовательность АВСВАС..., в которой не могут стоять рядом слои, обозначенные одинаковыми буквами.

Из множества возможных комбинаций в кристаллографии реальное значение име­ют два типа упаковки: 1) двухслойная упаковка АВАВАВ... — гексагональная плотноупакованная структура (рис. 108); 2) трехслойная упаковка АВСАВС... — кубическая гранецентрированная структура (рис. 109). В обеих решетках координационное число равно 12 и плотность упаковки одинакова — атомы занимают 74% общего объема кристалла. Координационное число, соответствующее кубической объемно центрированной решетке, равно 8, решетке алмаза (см. рис. 104) равно 4.

Кроме двух- и трехслойных упаковок можно построить многослойные с большим периодом повторяемости одинаковых слоев, например АВСВАСАВСВАС... — шестислойная упаковка. Существует модификация карбида SiC с периодом повторяемости 6, 15 и 243 слоя.

Если кристалл построен из атомов различных элементов, то его можно представить в виде плотной упаковки шаров разных размеров. На рис. 110 приведено модельное изображение кристалла поваренной соли. Крупные ионы хлора (r=181 пм) образуют плотную трехслойную упаковку, у которой большие пустоты заполнены меньшими по размеру ионами натрия (r=98 пм). Каждый ион Na окружен шестью ионами Сl и, наоборот, каждый ион Cl — шестью ионами Na.

§ 72. Дефекты в кристаллах

Рассмотренные в § 71 идеальные кристаллические структуры существуют лишь в очень малых объемах реальных кристаллов, в которых всегда имеются отклонения от упорядоченного расположения частиц в узлах решетки, называемые дефектами кристаллической решетки. Дефекты делятся на макроскопические, возникающие в процессе образования и роста кристаллов (например, трещины, поры, инородные макроскопи­ческие включения), и микроскопические, обусловленные микроскопическими отклонени­ями от периодичности.

Микродефекты делятся на точечные и линейные. Точечные дефекты бывают трех типов: 1) вакансии — отсутствие атома в узле кристаллической решетки (рис. 111, a); 2) междоузельный атом — атом, внедрившийся в междоузельное пространство (рис. 111, б); 3) примесный атом — атом примеси, либо замещающий атом основного веще­ства в кристаллической решетке (примесь замещения, рис. 111, в), либо внедрившийся в междоузельное пространство (примесь внедрения, рис. 111, б; только в междоузлии вместо атома основного вещества располагается атом примеси). Точечные дефекты нарушают лишь ближний порядок в кристаллах, не затрагивая дальнего порядка, — в этом состоит их характерная особенность.

Линейные дефекты нарушают дальний порядок. Как следует из опытов, механичес­кие свойства кристаллов в значительной степени определяются дефектами особого вида — дислокациями. Дислокации — линейные дефекты, нарушающие правильное че­редование атомных плоскостей.

Дислокации бывают краевые и винтовые. Если одна из атомных плоскостей об­рывается внутри кристалла, то край этой плоскости образует краевую дислокацию (рис. 112, а). В случае винтовой дислокации (рис. 112, б) ни одна из атомных плоскостей внутри кристалла не обрывается, а сами плоскости лишь приблизительно параллельны и смыкаются друг с другом так, что фактически кристалл состоит из одной атомной плоскости, изогнутой по винтовой поверхности.

Плотность дислокаций (число дислокаций, приходящихся на единицу площади поверхности кристалла) для совершенных монокристаллов составляет 10² — 10³ см^–2, для деформированных кристаллов — 10¹⁰ — 10¹² см^–2. Дислокации никогда не об­рываются, они либо выходят на поверхность, либо разветвляются, поэтому в реальном кристалле образуются плоские или пространственные сетки дислокаций. Дислокации и их движение можно наблюдать с помощью электронного микроскопа, а также методом избирательного травления — в местах выхода дислокации на поверхность возникают ямки травления (интенсивное разрушение кристалла под действием реаген­та), «проявляющие» дислокации.

Наличие дефектов в кристаллической структуре влияет на свойства кристаллов, анализ которых проведем ниже.

§ 73. Теплоемкость твердых тел

В качестве модели твердого тела рассмотрим правильно построенную кристалличес­кую решетку, в узлах которой частицы (атомы, ионы, молекулы), принимаемые за материальные точки, колеблются около своих положений равновесия — узлов решет­ки — в трех взаимно перпендикулярных направлениях. Таким образом, каждой состав­ляющей кристаллическую решетку частице приписывается три колебательных степени свободы, каждая из которых, согласно закону равнораспределения энергии по степеням свободы (см. § 50), обладает энергией kT.

Внутренняя энергия моля твердого тела

где N_A — постоянная Авогадро; N_Ak=R (R — молярная газовая постоянная). Молярная теплоемкость твердого тела

(73.1)

т. е. молярная (атомная) теплоемкость химически простых тел в кристаллическом

состоянии одинакова (равна 3R) и не зависит от температуры. Этот закон был эмпирически получен французскими учеными П. Дюлонгом (1785—1838) и Л. Пти (1791—1820) и носит названиезакона Дюлонга и Пти.

Если твердое тело является химическим соединением (например, NaCl), то число частиц в моле не равно постоянной Авогадро, а равно nN_A, где n — число атомов в молекуле (для NaCl число частиц в моле равно 2N_A, так, в одном моле NaCl содержится N_A атомов Na и N_A атомов Cl). Таким образом, молярная теплоемкость твердых химических соединений

т. е. равна сумме атомных теплоемкостей элементов, составляющих это соединение.

Как показывают опытные данные (табл. 4), для многих веществ закон Дю­лонга и Пти выполняется с довольно хорошим приближением, хотя некото­рые вещества (С, Be, В) имеют значи­тельные отклонения от вычисленных теплоемкостей. Кроме того, так же как и в случае газов (см. § 53), опыты по измерению теплоемкости твердых тел при низких температурах показали, что она зависит от температуры (рис. 113). Вблизи нуля кельвин теплоемкость тел пропорциональна Т³, и только при до­статочно высоких температурах, харак­терных для каждого вещества, выполня­ется условие (73.1). Алмаз, например, имеет теплоемкость, равную 3R при1800 К! Однако для большинства твердых тел комнатная температура является уже достаточно высокой.

Таблица 4

Расхождение опытных и теоретических значений теплоемкостей, вычисленных на основе классической теории, объяснили, исходя из квантовой теории теплоемкостей, А. Эйнштейн и П. Дебай.

§ 74. Испарение, сублимация, плавление и кристаллизация. Аморфные тела

Как в жидкостях, так и в твердых телах всегда имеется некоторое число молекул, энергия которых достаточна для преодоления притяжения к другим молекулам и кото­рые способны оторваться от поверхности жидкости или твердого тела и перейти в окружающее их пространство. Этот процесс для жидкости называетсяиспарением(илипарообразованием), для твердых тел —сублимацией (иливозгонкой).

Испарение жидкостей идет при любой температуре, но его интенсивность с повы­шением температуры возрастает. Наряду с процессом испарения происходит компен­сирующий его процесс конденсации пара в жидкость. Если число молекул, покидающих жидкость за единицу времени через единицу поверхности, равно числу молекул, перехо­дящих из пара в жидкость, то наступает динамическое равновесие между процессами испарения и конденсации. Пар, находящийся в равновесии со своей жидкостью, называ­ется насыщенным (см. также § 62).

Для большинства твердых тел процесс сублимации при обычных температурах незначителен и давление пара над поверхностью твердого тела мало; оно повышается с повышением температуры. Интенсивно сублимируют такие вещества, как нафталин, камфора, что обнаруживается по резкому, свойственному им запаху. Особенно интен­сивно сублимация происходит в вакууме — этим пользуются для изготовления зеркал. Известный пример сублимации — превращение льда в пар — мокрое белье высыхает на морозе.

Если твердое тело нагревать, то его внутренняя энергия (складывается из энергии колебаний частиц в узлах решетки и энергии взаимодействия этих частиц) возрастает. При повышении температуры амплитуда колебаний частиц увеличивается до тех пор, пока кристаллическая решетка не разрушится, — твердое тело плавится. На рис. 114, а изображена примерная зависимость Т (Q), где Q — количество теплоты, получа­емое телом при плавлении. По мере сообщения твердому телу теплоты его тем­пература повышается, а при температуре плавления T_пл, начинается переход тела из твердого состояния в жидкое. Температура T_пл остается постоянной до тех пор, пока весь кристалл не расплавится, и только тогда температура жидкости вновь начнет повышаться.

Нагревание твердого тела до T_пл еще не переводит его в жидкое состояние, поскольку энергия частиц вещества должна быть достаточной для разрушения кристал­лической решетки. В процессе плавления теплота, сообщаемая веществу, идет на совершение работы по разрушению кристаллической решетки, а поэтому T_пл = const до расплавления всего кристалла. Затем подводимая теплота пойдет опять-таки на увели­чение энергии частиц жидкости и ее температура начнет повышаться. Количество теплоты, необходимое для расплавления 1 кг вещества, называется удельной теплотой плавления.

Если жидкость охлаждать, то процесс протекает в обратном направлении (рис. 114, б; Q' — количество теплоты, отдаваемое телом при кристаллизации): сначала тем­пература жидкости понижается, затем при постоянной температуре, равной T_пл, начи­наетсякристаллизация, после ее завершения температура кристалла начнет понижаться. Для кристаллизации вещества необходимо наличие так называемыхцентров кристал­лизации — кристаллических зародышей, которыми могут быть не только кристаллики образующегося вещества, но и примеси, а также пыль, сажа и т. д. Отсутствие центров кристаллизации в чистой жидкости затрудняет образование микроскопических кри­сталликов, и вещество, оставаясь в жидком состоянии, охлаждается до температуры, меньшей температуры кристаллизации, при этом образуется переохлажденная жидкость (на рис. 114, б ей соответствует штриховая кривая). При сильном переохлаждении начинается спонтанное образование центров кристаллизации и вещество кристаллизу­ется довольно быстро.