
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Т е о р и я м е т о д а. Рассмотрим движение тела по наклонной плоскости длиною (рис.1)
Рассмотрим движение тела по наклонной плоскости длиною 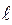 (рис.1). Тело, скатываясь с наклонной плоскости, участвуют в поступательном и вращательном движениях.
(рис.1). Тело, скатываясь с наклонной плоскости, участвуют в поступательном и вращательном движениях.
 рис.1.
рис.1.
| В точке А тело обладает запасом потенциальной энергии  По закону сохранения энергии, по-тенциальная энергия уменьшается и переходит в кинетическую энергию. В точке В тело приобрело кинетическую энергию поступа-тельного движения
По закону сохранения энергии, по-тенциальная энергия уменьшается и переходит в кинетическую энергию. В точке В тело приобрело кинетическую энергию поступа-тельного движения  и вращательного движения и вращательного движения 
|
По закону сохранения энергии  (1)
(1)
где υ - линейная скорость, ω - угловая скорость тела, J – момент инерции тел, h - высота наклонной плоскости. Теоретическая скорость
υТ определяется из соотношения (1). Для этого угловая скорость заменяется линейной с учетом формулы  , а момент инерции шара и цилиндра выражается формулами
, а момент инерции шара и цилиндра выражается формулами 

После постановки w и Jш, Jц в уравнение (1), получаем расчётные формулы скорости шара и цилиндра
 ,
, 
 (2)
(2)
Измерив высоту наклонной плоскости, вычисляем теоретические значения скоростей в точке В.
Экспериментальное определение скорости проводят так. В точке В тело имеет скорость υ, которая может быть представлена в виде двух компонент υх и υу – скорости в горизонтальном и вертикальном направлениях 

Из законов поступательного движения находим
х = 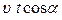 у =
у =  (3)
(3)
Время движения в обоих направлениях одинаково и равно  (4)
(4)
Подставив время (4) в уравнение (3), получим выражение для экспериментальной скорости в точке В
 (5)
(5)
а по найденному выражению скорости, окончательно находим время
 (6)
(6)
Дата добавления: 2014-10-31; просмотров: 364; Мы поможем в написании вашей работы!; Нарушение авторских прав |