
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 12. Электростатика
Еще в VII веке до нашей эры древнегреческий ученый Фалес обнаружил, что янтарь, потертый о шерсть, притягивает легкие предметы (расческа, электроскоп - примеры). Мы говорим, что тела наэлектризовываются или, тела при этом приобретают электрические заряды. Существуют два вида электрических зарядов: положительный «+» и отрицательный «-».
Заряды одного знака – отталкиваются, а заряды разных знаков – притягиваются. Электрический заряд любой системы тел состоит из элементарных частиц. Элементарные частицы: электрон – несущий отрицательный элементарный заряд, протон – положительный элементарный заряд, нейтрон – заряд, которого равно нулю.
qe = 1,6×10-19 Кл [q] = [Кл] = [А×с];
заряд электрона qe » заряду протона qпр, но масса протона mпр>2000 массы электрона me.
q = Sq+ + Sq- - закон сохранения электрического заряда
Из обобщения опытных данных установлено, что в изолированной системе алгебраическая сумма электрических зарядов остается постоянной – закон сохранения электрического заряда.
Система называется электрически изолированной, если между ней и внешними телами нет обмена электрическими зарядами.
Электрические заряды вокруг себя создают электрическое поле. Если же заряд неподвижен, то электрическое поле называется электростатическим.
Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих заряд.
Закон взаимодействия неподвижных точечных электрических зарядов был экспериментально установлен французским физиком Кулоном.
Сила, с которой взаимодействуют два точечных заряда, прямо пропорциональна произведению величин этих зарядов и обратно пропорциональна квадрату расстояния между этими зарядами
 :
:
В системе СИ k =1/4pe0 - коэффициент пропорциональности.
 Тогда - закон Кулона
Тогда - закон Кулона
e0 = 8,85×10-12 Ф/м - электрическая постоянная
Электрическое поле – особый вид материи, посредством которого взаимодействуют электрические заряды.

 Количественной характеристикой силового действия электрического поля является физическая величина – напряженность, определяемая формулой:
Количественной характеристикой силового действия электрического поля является физическая величина – напряженность, определяемая формулой:
- силовая характеристика
q0 пробныйточечныйзаряд электрического поля
 Пробный электрический заряд должен быть столь малым, чтобы его внесение в поле не вызывало изменения значений электрических зарядов.
Пробный электрический заряд должен быть столь малым, чтобы его внесение в поле не вызывало изменения значений электрических зарядов.
- напряженность электрического поля
 точечного заряда в вакууме.
точечного заряда в вакууме.
- напряженность электрического
 поля точечного заряда в среде.
поля точечного заряда в среде.
где e - диэлектрическая проницаемость среды.
Наглядно электрическое поле можно представить с помощью силовых линий.
Линией напряженности электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности.

| Линии напряженности не совпадают, не пересекаются, начинаются на положи-тельных зарядах и заканчиваются на отрицательных. | |

|  Электрическое поле однородно, если во всех его точках векторы Е одинаковы, т.е. имеют одинаковую густоту.
Электрическое поле однородно, если во всех его точках векторы Е одинаковы, т.е. имеют одинаковую густоту.
| |
Энергетической характеристикой электрического поля является потенциал- отношение WР точечного электрического заряда, помещенного в рассматриваемую точку поля, к этому заряду q:


Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной.
Определим работу, совершаемую силой F при перемещении точечного заряда из одной точки во вторую.
2 1 A = F×S
 q · · S = r1 –r2; F = qE
q · · S = r1 –r2; F = qE
r2 +q После преобразования
r1 А = qE (r1 –r2)
Известно, что A = -DWР
т.е. работа по перемещению заряда в электростатическом поле равна убыли потенциальной энергии заряда q в рассматриваемом поле.
Тогда

При перемещении электрического заряда в электростатическом поле работа сил поля равна произведению заряда на разность потенциалов начальной и конечной точек траектории движения заряда.
Мы знаем, что A = FDr = qEDr
С другой стороны A = -qDj Þ qEDr = -qDj

Изменение величины на единицу длины называется градиентом (grad) данной величины.
Е = - grad j - связь между силовой и энергетической
характеристиками электрического поля.
Поток вектора напряженности электрического поля – количество силовых линий, пронизывающих некоторую поверхность, расположенную перпендикулярно силовым линиям.
 S N = E×S
S N = E×S
n N = E×Scos a - однородное поле
a В случае неоднородного поля
dN = EdScos a

поток напряженности сквозь любую поверхность S равен алгебраической сумме потоков напряженности сквозь все малые участки этой поверхности.
Единица измерения потока вектора напряженности электростатического поля
[N] = [B×м]
Рассмотрим метод определения значения и направления вектора напряженности Е в каждой точке электростатического поля, создаваемого системой неподвижных зарядов q1, . . .qn.
Экспериментально было установлено, что результирующая сила F, действующая со стороны электрического поля на пробный заряд q, равна
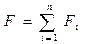 |
геометрической сумме сил Fi, приложенных к заряду q со стороны каждого из зарядов qi .
Нам известно, что Fi = qEi
где Еi – напряженность поля одного заряда qi
 Подставим значение силы F в предыдущую формулу и сократив на q, получим:
Подставим значение силы F в предыдущую формулу и сократив на q, получим:
- принцип суперпозиции (наложения)
электростатических полей.
Напряженность электрического поля системы точечных зарядов равна сумме напряженностей полей каждого из этих зарядов в отдельности – принцип суперпозиции полей.
Принцип суперпозиции позволяет рассчитать электрические поля любой системы неподвижных зарядов.
Согласно принципу суперпозиции электрических полей можно найти напряженность в любой точке поля двух точечных зарядов +q1 и -q2


 Сложение Е1 и Е2 производится
Сложение Е1 и Е2 производится
А по правилу параллелограмма.
 Направление результирующего
Направление результирующего
вектора Е находится построением,
а абсолютная величина определя
+q1 · ·-q2 ется по формуле:
Е = 
a - угол между Е1 и Е2
Вычисление Е поля системы электрических зарядов с помощью принципа суперпозиции можно упростить, используя теорему Гаусса, определяющую поток вектора напряженности электрического поля через произвольную замкнутую поверхность.
Определим поток вектора напряженности через замкнутую поверхность (случай сферической поверхности радиусом r, окружающий один точечный заряд).
 
|  Нам известно, что
Для сферической поверхности cosa = 1.
Нам известно, что
Для сферической поверхности cosa = 1.
 S = 4pr2 – площадь сферической поверхности S = 4pr2 – площадь сферической поверхности
|
 Таким образом, из каждого точечного заряда выходит поток вектора напряженности, равный q/ee0. Если n зарядов, то
Таким образом, из каждого точечного заряда выходит поток вектора напряженности, равный q/ee0. Если n зарядов, то
 |
- теорема Остроградского - Гаусса
Поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность равен сумме, заключенных внутри этой поверхности зарядов, деленный на электрическую постоянную e0 - теорема Остроградского – Гаусса.
Рассмотрим несколько случаев применения теоремы Остроградского – Гаусса для определения напряженности различных электростатических полей.
Вначале введем понятие о плотности зарядов.
Различают 3 вида: линейная, объемная и поверхностная плотности зарядов.

 Линейная плотность – физическая величина, характеризующая распреде-ление зарядов вдоль нити:
Линейная плотность – физическая величина, характеризующая распреде-ление зарядов вдоль нити:
 l – длина элемента нити.
l – длина элемента нити.
- при равномерном распределении заряда
 Объемная плотность - физическая величина, характеризующая распреде-ление зарядов по объему:
Объемная плотность - физическая величина, характеризующая распреде-ление зарядов по объему:
 |
- при равномерном распределении заряда
 Поверхностная плотность - физическая величина, характеризующая рас-пределение зарядов по площади:
Поверхностная плотность - физическая величина, характеризующая рас-пределение зарядов по площади:
 - при равномерном распределении заряда по площади
- при равномерном распределении заряда по площади
 1. Определим напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) в некоторой точке А на расстоянии r.
1. Определим напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) в некоторой точке А на расстоянии r.
Окружим часть нити длиной l1, воображаемым
l1 A цилиндром так, что боковая поверхность
содержит точку А.
r По теореме Остроградского - Гаусса
 |
С другой стороны N = E×S = E×2prl1, где S = 2prl1 - площадь боковой части цилиндра.
 Приравнивая правые части, получим
Приравнивая правые части, получим
 |
Отсюда - напряженность поля, создаваемого
бесконечно длинной равномерно
заряженной нитью.
2. Определим напряженность поля, создаваемого бесконечно равномерно заряженной плоскостью в некоторой точке А.
 Е Построим воображаемый цилиндр, ось
Е Построим воображаемый цилиндр, ось
А которого перпендикулярна плоскости,
а правое основание содержит точку А.
Плоскость делит цилиндр пополам.
По теореме Остроградского – Гаусса
 |
 Также N = E×2S, приравнивая правые части, находим:
Также N = E×2S, приравнивая правые части, находим:

отсюда
3. Напряженность поля, создаваемого двумя бесконечно параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.
 -s +s Напряженность поля между двумя
-s +s Напряженность поля между двумя
бесконечными
параллельными плоскостями равна сумме
 напряженности полей, создаваемых обоими
напряженности полей, создаваемых обоими
пластинами.
Вне пластин вектора Е от каждой из них направлены в противоположные стороны и взаимно уничтожаются.
Дата добавления: 2014-10-31; просмотров: 376; Мы поможем в написании вашей работы!; Нарушение авторских прав |