Тема 9. Статистические распределения

Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Этот закон теоретически выведен Максвеллом. Максвелл предположил, что газ состоит из очень большого числа N молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Закон Максвелла описывается функцией f (υ) – функция распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dυ, то на каждый интервал скорости приходит некоторое число молекул dN (υ), имеющих скорость, заключенную в этом интервале. Функция f (υ) определяет относительное число молекул dN (υ)/ N, скорости которых лежат в интервале от υ до υ+dυ, , т.е.

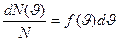
Отсюда

Применяя методы теории вероятностей, Максвелл получил функцию

- закон о распределении молекул идеального газа по скоростям

Вид функции зависит от рода газа (m₀.- массы молекулы) и от температуры. Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью

Исходя из распределения молекул по скоростям, можно найти распределение молекул по энергиям теплового движения

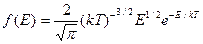
Проинтегрировав это выражение, получим среднюю кинетическую энергию молекул идеального газа

При выводе основного уравнения МКТ и максвелловского распределения, предполагалось, что на молекулы газа не действуют внешние силы, поэтому молекулы равномерно распределены по объему. Мы знаем, что молекулы любого газа находятся в поле тяготения Земли и давление газа с высотой убывает по закону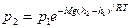

Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то можно записать

- барометрическая формула

р – давление на высоте h.

Используя формулу р = n kT , барометрическую формулу можно преобразовать

n – концентрация молекул на высоте h

n₀ - концентрация молекул на высоте h=0

Так как М = m₀N_A , а R = kN_A

то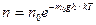

где Е_p = m₀gh - потенциальная энергия в поле тяготения

Тогда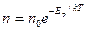

- распределение Больцмана для внешнего потенциального поля.