Тема 3. Принцип относительности в механике

Если системы отсчета движутся относительно друг друга прямолинейно и равномерно, и в одной из них справедливы законы Ньютона – инерциальные системы отсчета. Во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму - суть механического принципа относительности (принцип относительности Галилея).

Рассмотрим две системы отсчета: неподвижную инерциальную систему К (с координатами X, Y ,Z) и К1 (x1, y1, z1), движущуюся относительно К прямолинейно и равномерно со скоростью и (u = const). Отсчет t начнем с момента, когда начало координат совпадает со скоростью и направлена вдоль ОО1, тогда радиус – вектор, проведенный из О в О1 r0 = u × t

Определим связь между координатами точки А в обеих системах

r = r¹ + r₀ = r¹ + u × t

В проекциях на оси координат:

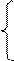X = x¹ + u_xt

Y = y¹ + u_yt - преобразования координат Галилея

Z = z¹ + u_zt

В классической механике ход времени не зависит от относительного движения систем отсчета, тогда можно записать t = t¹

Преобразования Галилея справедливы только при u << с, а при u @ с – заменяются преобразованиями Лоренца.

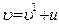Известно - правило сложения скоростей в классической механике.

Ускорение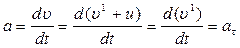

Таким образом, ускорение точки А в системе отсчета К и К¹, движущихся равномерно друг относительно друга прямолинейно и равномерно одинаково.

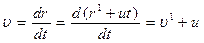Следовательно, при переходе от одной инерциальной системы отсчета к другой уравнения динамики не изменяются, т.е. являются инвариантными по отношению к преобразованиям координат.

При u @ с преобразования Галилея несправедливы. Нужно было создать новую механику, которая содержала бы ньютоновскую механику как предельный случай для малых скоростей (u<< с). Это удалось, сделать А. Эйнштейну – он заложил основы специальной теории относительности. Специальная теория относительности также называется релятивистской теорией.

В основе специальной теории относительности лежат постулаты Эйнштейна: принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы относительности к другой, т.е. любые физические явления протекают одинаково во всех инерциальных системах отсчета.

принцип инвариантности скорости света: скорость света в вакууме предельна и одинакова во всех инерциальных системах отсчета.

Эйнштейн показал, что в теории относительности классические преобразования Галилея заменяются преобразованиями Лоренца, которые имеют вид:

y¹ = y

z¹ = z

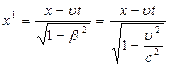При малых скоростях преобразования Лоренца переходят в преобразования Галилея – принцип соответствия.

Следствия из преобразования Лоренца:

1. Координаты х, х¹ и время t, t¹ не могут быть мнимыми, т.е. подкоренное выражение должно быть больше нуля.

Следовательно, u/с <<1, т.е. u относительного движения двух инерциальных систем отсчета не может превосходить с.

2. События, происходящие одновременно в разных местах системы К при наблюдении их из системы К¹, движущейся относительно К, могут казаться разновременными – нарушение одновременности удаленных событий

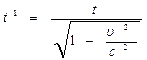3. Интервал времени становится функцией скорости системы

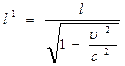4. Длина тел

Таким образом, длина, измеренная в системе, относительно которой он движется, оказывается меньше длины измеренной в системе, относительно которой стержень покоится.

5. Пусть скорость тела внутри ракеты – u¹, ракета имеет скорость u по отношению к Земле. Определим скорость u движения тела с точки зрения земного наблюдателя.

Тогда релятивистский закон сложения скоростей:

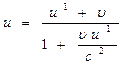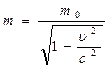6. Относительность масс

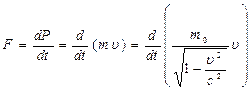Тогда основной закон динамики

Следовательно 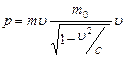- релятивистский импульс

Мы знаем, законы Ньютона выполняются в инерциальных системах отсчета. Системы отсчета, движущиеся относительно инерциальной системы с ускорением, называется неинерциальными. В неинерциальных системах отсчета законы Ньютона несправедливы. Но можно применить, если кроме сил обусловленных воздействием тел друг на друга, ввести в рассмотрение силы особого рода – силы инерции.

Если учесть силы инерции, то II закон Ньютона будет справедлив для любой системы отсчета. В данном случае

ma¹ =F +F_ин,

т.е. произведение массы тела на его ускорение равно сумме всех сил, действующих на тело, включая F_ин.