Тема 11. Реальные газы. Явления переноса

Реальный газ – газ, где учитываются объем (размеры) и силы взаимодействия молекул. Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И.Ван-дер-Ваальс введя поправки в уравнение Менделеева-Клайперона, вывел уравнение состояния реального газа.

Уравнение состояния для 1 моля идеального газа имеет вид pV = RT

Согласно этой формуле объем газа при сжатии может стать равным нулю. В случае реальных газов часть объема занята самими молекулами. Поэтому объем, занимаемый газом, должен быть уменьшен на величину b, где b- объем занимаемый самими молекулами, т.е. (V-b). Таким образом, b –постоянная величина, учитывающая объемы (размеры) молекул. В реальных газах имеются силы взаимного притяжения молекул, которые действуют дополнительно к силам внешнего давления и как бы сжимают газ. Вследствие этого возникает добавочное внутреннее давление p_i, т.е.

где (p + p_i), а – постоянная величина, учитывающая

силы межмолекулярного притяжения

Тогда, введя поправки на V и p, получим уравнение состояния реального газа

- уравнение Ван-дер-Ваальса для 1 моля газа

Величины a и b для различных газов различны и их значение приводятся в справочных таблицах.

Для любой массы газа

Уравнение Ван-дер-Ваальса не единственное уравнение, описывающее реальные газы. Существуют и другие уравнения, некоторые из них даже точнее описывают реальные газы, но не рассматриваются из-за их сложности.

Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса – кривые зависимости давления p от объема V при заданных температурах Т, определяемые уравнение Ван-дер-Ваальса для 1 моля газа.

Эти кривые рассматриваются для четырех различных температур и имеют своеобразный характер.

Задавая различные температуры T1 > T2 > T3 > T4 > T5 получим семейство изотерм Ван-дер-Ваальса. При высоких температурах изотерма реального газа отличается от изотермы идеального газа только некоторым искажением формы. Изобара AD пересекает изотерму в одной точке. Это означает, что каждому значению давления и температуры

соответствует единственное значение объема, т.е. при высоких температурах вещество находится в однофазном – газообразном состоянии. Невысоким температурам соответствуют изотермы 2-, 3-, 4, на которых имеются изгибы.

Изобара AD пересекает изотерму 4 в трех точках А, В, С. Это означает, что вещество одновременно находится в трех фазовых состояниях. Переход от изотермы 5 к изотермам 4,3,2,1, соответствующий повышению температуры, приводит к тому, что изгибы на изотермах сглаживаются. Расстояние между точками А и С уменьшаются и на изотерме 2 сливаются в одну точку К. Здесь р_К = const является касательной к изотерме. Эта изотерма называется критической, соответствующая температура Т_к – критической , точка К – критической. Соответствующие этой точке V_K и р_К – называются критическими.

Состояние с критическими параметрами (V_K,,р_К,,Т_К) называются критическим состоянием.

Температурам, выше критическим соответствует только газообразное состояние вещества. Следовательно, критическая температура Т_К – это наивысшая температура, при которой газ может еще может быть превращен в жидкость. При критическом состоянии вещества различия в свойствах пара и жидкости отсутствуют. Критические состояния характеризуется непрерывным переходом пара в жидкость и жидкости в пар.

Мы знаем, что U = U₁ + U₂ = E_к + E_р.

В случае реального газа, помимо кинетической энергии Е_к нужно учитывать потенциальную энергию Е_р взаимодействия молекул.

Внутренняя энергия для 1 моля идеального газа

Так как , то

Работа сил молекулярного сцепления равна: dA = p_i dV,

Мы знаем, что

Тогда dU которое произошло за счет совершения работы

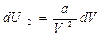или интегрируя, получим:

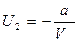- потенциальная энергия

Тогда - внутренняя энергия 1 моля реального газа.

Следовательно, внутренняя энергия реального газа зависит как от температуры, так и от его объема.

В термодинамически неравновесных системах возникают особые необратимые процессы – явления переноса – в результате которых происходит пространственный перенос энергии, массы, импульса.

К явлениям переноса относятся:

1. Теплопроводность обусловлена переносом энергии (горячий чай – холодная ложка). Если в одной области Е_к молекул больше, чем в другой, то в процессе столкновений молекул с течением времени происходит выравнивание кинетической энергии, т.е. температур.

Перенос энергии в форме теплоты подчиняется закону Фурье

j_E – плотность теплового потока – энергия, переносимая в форме теплоты через единицу площади в единицу времени, перпендикулярную оси х.

- коэффициент теплопроводности

– градиент температуры – изменение температуры на единицу длины. «-» - при теплопроводности энергия переносится в направлении убывания температуры.

2. Диффузия - самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и твердых тел.

Явление диффузии подчиняется закону Фика

j_m – плотность потока массы – масса вещества, диффундирующего в единицу времени через единицу площади, перпендикулярную оси х

D – коэффициент диффузии

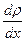- градиент плотности, «-» показывает, что перенос массы происходит в направлении убывания плотности.

Согласно кинетической теории газов

3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Сила трения между слоями подчиняется закону Ньютона

Тогда от одного слоя к другому передается импульс, по модулю равный действующей силе

j_p – плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х.

- градиент скорости, «-» - указывает, что импульс переносится в направлении убывания скорости.

Динамическая вязкость определяется по формуле

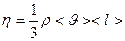
Коэффициенты переноса связаны между собой соотношениями

и