
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 10. Основы термодинамики
I закон термодинамики известен со школьного курса физики
Q = DU + A - I закон термодинамики или закон сохранения и превращения энергии в термодинамике.
Теплота, сообщаемая системе, расходуется на изменение внутренней энергии и на совершение работы против внешних сил.
В дифференциальной форме:
dQ = dU + dA
В более корректной форме:
¶Q = dU + ¶A
dU – бесконечно малое изменение внутренней энергии.
¶A – элементарная работа
¶Q – бесконечно малое количество теплоты
dU является полным дифференциалом, а ¶A и ¶Q – таковыми не являются.
Внутренняя энергия – важная характеристика термодинамической системы – энергия движения и взаимодействия частиц, из которых состоит тело
U = Eк + Ep
Для идеального газа Ер = 0, тогда U = Eк или

 Þ
Þ
Работа, совершаемая, газом при изменении объема определяется по формуле

| δA = pdV
 Полная работа, совершаемая газом при изменении объема от V1 до V2 определим интегрированием Полная работа, совершаемая газом при изменении объема от V1 до V2 определим интегрированием
|
Полная работа определяется площадью, ограниченной осью абсцисс.
В термодинамике для характеристики тепловых свойств тел используется понятие теплоемкости.
Известно, теплота Q, переданная или отданная телом определяется по формуле

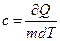 Q = mcDT где с – удельная теплоемкость
Q = mcDT где с – удельная теплоемкость
| - теплота, необходимая для нагревания вещества массой 1 кг на 1 К. |
Помимо удельной теплоемкости часто целесообразно использовать молярную теплоемкость

 - теплота, необходимая для нагревания
- теплота, необходимая для нагревания
1 моля вещества на 1 К.
Удельная теплоемкость связана с молярной теплоемкостью соотношением:
Сm = с×m
Различают теплоемкости при V = const и p = const
 | 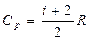 |
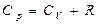 - уравнение Майера
- уравнение Майера
показывает, что Ср > CV на R.. Это объясняется тем, что при нагревании газа при p = const требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.
При рассмотрении термодинамических процессов важно знать характерное для каждого газа отношение Ср /СV

где i - число степеней свободы.
Адиабатный процесс – процесс, протекающий без теплообмена с окружающей средой - ¶Q = 0 – все быстропротекающие процессы.
Адиабатные процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах); процесс распространения звука в среде.
 р Адиабатный процесс описывается
р Адиабатный процесс описывается
уравнением Пуассона
-адиабата pVg = const
-изотерма где g - показатель адиабаты.
V
Рассмотренные изохорный, изобарный, изотермический и адиабатный процессы имеют общую особенность – происходят при постоянной теплоемкости.
Процесс, в котором теплоемкость остается постоянной называется политропным.
Уравнение политропы pV n = const
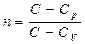 |
где - показатель политропы
Очевидно, что при С = 0, n = g - уравнение адиабаты
при С = ¥, n = 1 - уравнение изотермы
при С = Ср, n = 0 - уравнение изобары
при С = СV n = ± ¥, - уравнение изохоры
Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.
Рассмотрим применение I закона термодинамики к различным процессам:
1. Т= const – изотермический процесс dU = 0; ¶Q = ¶A
 Вся теплота, сообщаемая газу, расходуется на совершение им работы против внешних сил
Вся теплота, сообщаемая газу, расходуется на совершение им работы против внешних сил
2. p = const – изобарный процесс ¶Q = dU + ¶A
 | |||||
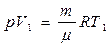 | |||||
 | |||||
 Þ
Þ
 |

Тогда - работа газа при изобарном процессе
Отсюда физический смысл газовой постоянной R: Т2 –Т1 = 1К, то для 1 моля газа R = A, т.е. R численно равно работе изобарного расширения 1 моля идеального газа при нагревании его на 1К.
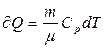 В изобарном процессе при сообщении газу массой m количества теплоты
В изобарном процессе при сообщении газу массой m количества теплоты
 его внутренняя энергия возрастает на величину
его внутренняя энергия возрастает на величину
 |
При этом газ совершает работу
3. V = const - изохорный процесс
 Газ не совершает работы над внешними силами
Газ не совершает работы над внешними силами
 |
4. ¶Q = 0 – адиабатный процесс

Тогда ¶A = - dU т.е. внешняя работа совершается за счет изменения внутренней энергии.
Круговой процесс – процесс, при котором система, пройдя через ряд состоя-ний, возвращается в исходное состояние.
 p
p
1 · 1 – a – 2 – расширение газа
b
а 2 – b – 1 – сжатие газа
·2
V
V 1 V2
Работа, совершаемая газом за цикл, определяется площадью охватываемой замкнутой кривой.
Если круговой процесс идет по часовой стрелке, то работа будет положительной - прямой цикл, если же против часовой стрелки, то работа отрицательна – обратный цикл.
Прямой цикл используется в тепловых двигателях – совершающих работу за счет полученной извне теплоты. Обратный цикл используется в холодильных машинах – в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой.
В результате кругового процесса система возвращается в исходное состояние и DU = 0. И тогда I закон термодинамики Q = A, т.е. работа, совершаемая за цикл, равна количеству тепла, полученной извне.
Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому Q = Q1 – Q2
где Q1 – тепло полученное системой Q2 - тепло отданное системой.
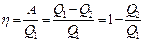 Поэтому
Поэтому
- к.п.д. для кругового процесса.
Процесс, который может самопроизвольно протекать как в прямом, так и в обратном направлениях называется обратимым. Примером обратимого процесса могло бы служить колебание маятника, если бы оно происходило без трения. Все механические процессы, происходящие, без трения были бы обратимые, однако трение не устранимо.
Необратимым называется процесс, который нельзя провести в обратном направлении через те же промежуточные состояния: сжатие и расширение газа, диффузия газов.
Энтропия наряду с энергией является важной характеристикой состояния термодинамической системы. Энтропия является величиной, с помощью которой учитывают потери и рассеяние теплоты, происходящие в реальных процессах, превращение теплоты в другие виды энергии при теплообмене.
Но чаще интересует изменение энтропии так как оно определяет обратимость или необратимость процессов в изолированной системе.
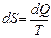 |  | ||
Для обратимых процессов изменение энтропии DS = 0
Для необратимых процессов DS > 0, т.е. энтропия системы возрастает.
Энтропия - определяет только состояние системы и не зависит от пути, каким система пришла в это состояние.
I закон термодинамики устанавливает количественное соотношение при превращении теплоты в механическую работу.
II закон термодинамики определяет направление развития процессов: естественные процессы протекают в сторону увеличения энтропии. Наиболее общее выражение II закона термодинамики: в изолированной системе при всех реальных процессах энтропия возрастает, или невозможен процесс, единственным результатом которого является превращение в работу теплоты, взятой от нагревателя, т.е.
A < Q1 - II закон термодинамики
Таким образом, тепловая машина должна работать по схеме:
| Нагреватель Т1 |
 Q1
Q1
| Рабочее тело |
A=Q1-Q2
Q2
| Холодильник Т2 |
II закон термодинамики доказывает невозможность создания вечного двигателя.
Основываясь на II закон термодинамики, и анализируя работу тепловых двигателей, французский инженер Карно пришел к выводу, что наивыгоднейшим круговым процессом является обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов, так как он характеризуется наибольшим к.п.д. Такой цикл и получил название цикла Карно. Процесс протекает в идеальной тепловой машине – машине, которая действует без трения, т.е. без необратимых потерь.

| 1 - 2; 3 – 4 – изотермы
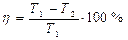 2 – 3; 4 – 1 – адиабаты
- к.п.д. идеальной тепловой машины, работающей по циклу Карно 2 – 3; 4 – 1 – адиабаты
- к.п.д. идеальной тепловой машины, работающей по циклу Карно
|
Таким образом, для цикла Карно к.п.д. определяется только температурами нагревателя и холодильника и не зависит от состава рабочего тела.
Дата добавления: 2014-10-31; просмотров: 355; Мы поможем в написании вашей работы!; Нарушение авторских прав |