
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Т е о р и я м е т о д а. Физическим маятником называется твердое тело, способное совершать колебания под действием силы тяжести вокруг неподвижной оси
Физическим маятником называется твердое тело, способное совершать колебания под действием силы тяжести вокруг неподвижной оси, не проходящей вокруг центра тяжести (рис.1).
Вращение твердого тела характеризуется моментом силы, моментом инерции и угловым ускорением, которые связаны между собой
М = J × e (1)
Момент инерции твердого тела есть мера его инертности при вращательном движении и измеряется суммой произведений масс точек тела на квадраты их расстояний до оси вращения
J =  (2)
(2)
Для тел правильной геометрической формы момент инерции вычисляется интегрированием. Для тел неправильной геометрической формы – экспериментально. Примером физического маятника является тракторный шатун.
Если физический маятник отклонить на угол j, то на него будут действовать сила тяжести Р в центре тяжести С и сила реакции опоры N в точке 0. Ввиду того, что векторы этих сил не направлены по одной прямой, действие их не скомпенсировано. Если спроектировать силу тяжести на оси х и у, то проекция Рх является возвращающей силой, момент которой равен
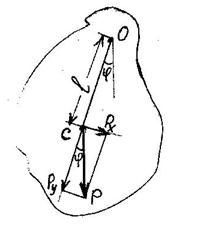
| М = - Р х l; где Р х = Р × sinφ М = - mgl sinj
где j - угол отклонения, не превышающий 3-50.
Так как угол отклонения мал, то значение sinj можно заменить значением угла, т.е. sinj » j. Теперь момент силы будет равен:
М = - mgl× j (3)
Момент силы сообщает маятнику угловое ускорение, которое определяется как вторая производная от угла поворота

|
Приравнивая значение моментов сил (уравнения (1) и (3)) получим дифференциальное уравнение второго порядка:
J  Þ
Þ 
Произведение  равно квадрату угловой скорости w2. Угловая скорость связана с периодом обращение Т =
равно квадрату угловой скорости w2. Угловая скорость связана с периодом обращение Т = 
Тогда Т=2p 
и момент инерции будет равен J = 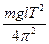
относительно оси, проходящей через точку 0.
По теореме Штейнера определяем момент инерции относительно центра
тяжести С: J =Jc + md2 где d = l,
Jc = J – md2
Дата добавления: 2014-10-31; просмотров: 370; Мы поможем в написании вашей работы!; Нарушение авторских прав |