Геометрические построения. Контуры изображаемых деталей образуют линии – прямые, коробовые и лекальные кривые

Контуры изображаемых деталей образуют линии – прямые, коробовые и лекальные кривые. При вычерчивании изображений применяют следующие построения:

- деление отрезков и углов;

- деление окружности на равные части;

- сопряжения линий;

- построение уклона и конусности.

2.1. Деление отрезка прямой

2.1.1. Деление отрезка пополам

Деление отрезка пополам выполняют следующим образом (рисунок 10а):

- из точек A и B радиусом R > 0,5AB проводят дуги до пересечения в точках C и D;

- через точки C и D проводят прямую линию, которая делит отрезок пополам (точка E).

а) б) в)

Рисунок 10 – Деление отрезка

2.1.2. Деление отрезка на равные части

Деление отрезка на равные части выполняют следующим образом (рисунок 10б):

- из точки A отрезка AB под произвольным углом проводят прямую линию и делят ее на заданное число равных отрезков (точки 1, 2, 3, C);

- точку C соединяют с точкой B;

- из точек 1, 2, и 3 проводят прямые параллельно отрезку BC, до пересечения с отрезком AB в точках 1', 2' и 3'.

2.1.3. Деление отрезка на пропорциональные части

Деление отрезка на пропорциональные части выполняют в следующей последовательности (рисунок 10в):

- из точки A отрезка AB под произвольным углом проводят прямую линию и делят ее на равные части, например, три;

- точку C соединяют с точкой B;

- из точки D проводят прямую параллельно отрезку BC.

2.2. Деление угла на две равные части

Деление угла на равные части выполняют в следующей последовательности (рисунок 11):

- из вершины угла B произвольным радиусом R проводят дугу до пересечения со сторонами угла в точках D и C;

- из точек D и C радиусом R₁ проводят дуги до пересечения в точке K;

- соединяют точки B и K (отрезок BK делит угол пополам).

Рисунок 11 – Деление угла Рисунок 12 – Деление окружности

2.3. Деление окружности на равные части

Пример деления окружности на равные части проведен на рисунке 12.

Справа от оси CD показано деление окружности на три, шесть и двенадцать частей, для чего:

- из точки A радиусом R окружности проводят дугу до пересечения с окружностью в точках F и E. Отрезок FE отсекает треть окружности, AF – шестую, а DF – двенадцатую часть окружности.

Слева над осью АВ показано деление окружности на пять и десять частей (выше оси AB), для чего:

- из точки A радиусом R окружности проводят дугу до пересечения с окружностью в точках F и E;

- из точки E строят перпендикуляр до пересечения с осью AB (точка) O₁;

- из точки O₁ радиусом R₁=O₁C проводят дугу до пересечения с

осью AB (точка М). Отрезок CM делит окружность на пять, а отрезок OM на десять равных частей.

Слева ниже оси AB показано деление окружности на четыре и восемь равных частей, для чего:

- соединяют точки B и D;

- делят отрезок BD пополам (см. пункт 2.1.1);

- из центра O проводят серединный перпендикуляр до пересечения с окружностью (точка K). Отрезок BD делит окружность на четыре, а отрезок KD – на восемь равных частей.

2.4. Построение треугольника

Пример построения треугольника по трем заданным сторонам приведен на рисунке 13.

Рисунок 13 – Построение треугольника

Из концов стороны АС треугольника радиусами R=n и R₁=m проводят дуги до пересечения в точке В. Полученную точку соединяют с точками А и С.

2.5. Построение уклона

Уклоном iпрямой АС относительно прямой АВ называется тангенс угла между этими прямыми, т.е. i = (h/l) = tga, где h – разность аппликат концов отрезка АС; l– разность абсцисс отрезка АВ (рисунок 14).

Уклон на чертеже в соответствии с ГОСТ 2.307 - 68 указывают с помощью линии-выноски, на полке которой наносят знак и значение уклона.

Уклон обозначается знаком « Ð », а величина его выражается дробью, в процентах и градусах, например, Ð 1:5, Ð 20 %, Ð 15⁰. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть параллельна катету (АВ), а другая - наклонена под углом 30⁰ к ней, при этом острие знака всегда направлено в сторону уклона.

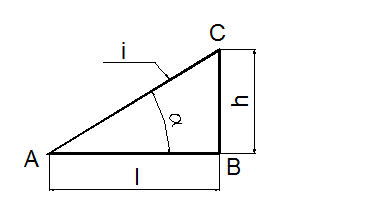
Рисунок 14 – Опре- Рисунок 15 – Обозначение уклона

деление величины уклона

2.6. Построение конусности

Конусностью C называется отношение диаметра окружности основания прямого конуса к его высоте C = D/2H = tga/2 (рисунок 16).

Конусность на чертеже в соответствии с ГОСТ 2.307 - 68 указывают с помощью линии-выноски, на полке которой наносят знак и значение конусности.

Рисунок 16 – Опреде- Рисунок 17 – Обозначение

ление конусности конусности

Построение усеченного конуса с заданным диаметром большего основания D, высотой H и конусностью равной 1:4 (рисунок 18) выполняется в следующей последовательности:

- откладываем высоту конуса H=ОО₁ на оси симметрии;

- через точку O проводим перпендикуляр, на котором симметрично от оси откладываем диаметр большого основания D=BC;

- из точки O по оси OO₁ откладываем четыре равных отрезка произвольной длины OA=4a;

- от точки O симметрично от оси откладываем отрезок a=FE;

- соединив точки F и E с точкой A, получим вспомогательный конус с конусностью 1:4;

- через точки B и C проводим прямые линии параллельно образующим вспомогательного конуса до пересечения с перпендикуляром, проведенным через точку O₁. Полученные точки K и L ограничивают величину малого основания усеченного конуса.

2.7. Сопряжения

Очертание многих деталей, узлов состоит из линий, плавно переходящих одна в другую, называемых сопряжением. Из многообразия возможных сопряжений можно выделить следующие:

- сопряжение двух прямых линий дугой окружности;

- сопряжение прямой линии с дугой окружности при помощи другой дуги окружности;

- сопряжение двух дуг окружности при помощи третьей дуги.

Рисунок 18 – Построение Рисунок 19 – Сопряжение конусности сторон угла

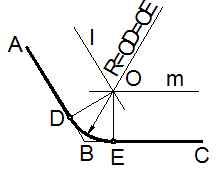
2.7.1. Сопряжение двух прямых линий

Сопряжение двух сторон угла дугой окружности (рисунок 19) выполняется следующим образом:

- параллельно сторонам угла AB и BC на расстоянии равном радиусу дуги R проводят прямые линии l и m до пересечения в точке О;

- из точки O опускают перпендикуляры на сопрягаемые стороны. Точки D и E являются точками сопряжения;

- из точки O радиусом R = OD = OE проводят дугу плавно переходящую в прямые линии.

2.7.2. Сопряжение прямой линии с дугой окружности

Рассмотрим два случая сопряжения: внешнее и внутреннее.

Внешнее сопряжение прямой линии с дугой окружности выполняется следующим образом:

- из центра О строится дуга радиусом R₂=R+R₁, где R₁ – радиус сопряжения;

- на расстоянии R₁ от заданной прямой n проводится параллельная прямая m;

- определяется центр О₁ сопряжения как результат пересечения дуги окружности радиусом R₂ с прямой m;

- из центра О₁ строится дуга AB сопряжения радиусом R₁.

Внутреннее сопряжение прямой с дугой окружности выполняется так:

- из заданного центра заданной дуги окружности строится дуга радиусом R₂=R-R₁, где R₁ – радиус сопряжения;

- на расстоянии R₁ от заданной прямой n проводится параллельная прямая m;

- из полученного центра О₁ строится дуга AB сопряжения радиусом R₁.

а) б)

Рисунок 20 – Сопряжение дуги окружности с прямой линией

2.7.3. Сопряжение двух дуг окружности

Различают внешнее, внутреннее и смешанное сопряжение двух дуг третьей дугой. Во всех трех случаях необходимо определить положение центра дуги сопряжения О₂ и точек сопряжения A и B.

Внешнее сопряжение (рисунок 21а) выполняется следующим образом:

- из центров дуг окружностей О и О₁ радиусами R₃=R+R₂ и R₄=R₁+R₂ соответственно, проводим дуги до их пересечения в точке О₂;

- соединяем центр сопряжения О₂ с центрами дуг окружностей прямыми линиями О₂О и О₂ О₁;

- из центра сопряжения О₂ радиусом R₂ проводим дугу между точками сопряжения A и B.

а) б) в)

Рисунок 21 –Сопряжение двух дуг окружностей

Пример выполнения внутреннего сопряжения приведен на рисуноке 21б):

- из центров дуг окружностей О и О₁ радиусами R₃= R₂-R и R₄=R₂- R₁ проводим дуги до их пересечения в точке О₂;

- соединяем центр сопряжения О₂ с центрами дуг окружностей прямыми линиями О₂О и О₂ О₁;

- из центра сопряжения О₂ радиусом R₂ проводим дугу между точками сопряжения A и B.

Смешанное сопряжение (рисунок 21в) выполняется следующим образом:

- из центров дуг окружностей О и О₁ радиусами R₃=R+R₂ и R₄=R-R₂ соответственно, проводим дуги до их пересечения в точке О₂;

- соединяем центр сопряжения О₂ с центрами дуг окружностей прямыми линиями О₂О и О₂ О₁;

- из центра сопряжения О₂ радиусом R₂ проводим дугу между точками сопряжения A и B.