
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Конспект лекций по дисциплине
План
3.1 Функція витрат
3.2 Функції попиту
3.3 Функції пропозиції
3.4 Функція корисності споживача
3.1 Аналіз витрат містить вивчення впливу витрат виробництва на обсяг виробництва й інші техніко-економічні показники. Найчастіше розглядається функція вигляду:
 ,
,
де Z - сумарні витрати;
x - кількість продукції;
 - параметри моделі;
- параметри моделі;
vi - інші змінні, що характеризують різну структуру ОВФ, різні умови виробництва, різну організацію праці в різних галузях.
Поділимо обидві частини виразу на х

 ,
,
де  питомі витрати.
питомі витрати.
Графік питомих витрат показано на рис. 3.1.
Відвернемося від впливу факторів, що, можливо при вивченні витрат у загальнодержавних масштабах. Тоді
Z=f(x),
 ,
,

Рис. 3.1
Лінійна функція витрат має вигляд:
Z=f(x)=b0+bix.
Функція питомих витрат буде спадаючою. Параметри можна інтерпретувати за допомогою граничних величин
 ,
,
тепер перейдемо від неперервної форми до дискретної
 ,
,
тобто фактор ∆Vi при незмінному рівні випуску продукції збільшує витрати на ∆Z ,
∆Z=b i ∆Vi.,
Якщо ∆Vi=1, то ∆Z=bi..
3.2 Функція попиту виражає залежність попиту від економічних (доходи, ціни) і зовнішньоекономічних (споживчі звички) факторів. Функції попиту можуть бути як макроекономічними, якщо охоплюють усю сферу споживання і мікроекономічними, що описують попит індивідуальних споживачів.
D(p) - функція попиту або просто попит (від англ. “demand” - попит) – це кількість товару, що купується на даному ринку за одиницю часу за ціною p за одиницютовару. Фундаментальну властивість функції попиту виражає наступна аксіома: функція попиту є спадаючою, при збільшенні ціни величина попиту на товар зменшується до 0, при зменшенні ціни товару величина попиту збільшується.
Розглянемо наступні функції попиту (рис 3.2):
а) лінійно-спадаюча
D (p) =а-bp,  , (a,b)>0,
, (a,b)>0,
б) обернена
D (p)=1/p, р>0,
в) логарифмічна
D (p)=ln (1+p)/p , p>0.



a) б) в)
Рис.3.2
Розглянемо математичні характеристики функції попиту та їхні економічні ілюстрації. Похідна функції попиту за ціною
 ,
,
показує наскільки одиниць зміниться величина попиту при зміні ціни товару на одну одиницю.
Еластичність попиту за ціною показує на скільки відсотків зміниться величина попиту при зміні ціни товару на один відсоток. Позначається еластичність
 .
.
3.3 S(p) - функція пропозиції або пропозиція (від англ.“supply” - пропозиція) – це кількість товару, що поставляється на даний ринок за одиницю часу при ціні р за одиницю товару). Функція пропозиції є зростаючою. Аксіома пропозиції: при збільшенні ціни величина пропозиції товару необмежено збільшується, при зменшенні ціни величина пропозиції зменшується, наближаючись до 0.
Розрізняють функції пропозиції (рис. 3.3):
а) лінійно-зростаюча
S (p) = -c + dp,  ,
,
б) степенева
 ,
,
в) логарифмічна
 .
.



а) б) в)
Рис. 3.3
Розглянемо математичні характеристики функції пропозиції та їхні економічні ілюстрації.
Похідна функції за ціною
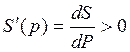 ,
,
показує на скільки відсотків зміниться величина пропозиції при зміні ціни товару на одну одиницю.
Еластичність пропозиції за ціною показує на скільки відсотків зміниться пропозиція при зміні ціни товару на один відсоток. Позначається еластичність
 .
.
Знайдемо еластичність пропозиції за ціною для кожної функції, що розглянута вище:
a)  ,
,
 ;
;
б)  ,
,
 ;
;
в)  ,
,
 .
.
3.4 Рішення споживача щодо купівлі певного набору товарів математично можна подати як вибір точки у просторі товарів. Нехай
n — скінченне число видів різноманітних товарів,

де Di – обсяг товару i-го виду, 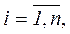

 - вектор-стовпець споживчих товарів (обсяги), що їх придбав споживач за певний термін (наприклад протягом року) за заданих цін, маючи певний обсяг доходу за цей самий період.
- вектор-стовпець споживчих товарів (обсяги), що їх придбав споживач за певний термін (наприклад протягом року) за заданих цін, маючи певний обсяг доходу за цей самий період.
Це означає, що для кожної пари товарів має місце одне з трьох відношень,  :
:

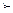
 — набір
— набір  є привабливішим, ніж
є привабливішим, ніж  ;
;


 — набір
— набір  є менш привабливим, ніж
є менш привабливим, ніж  ;
;
 ~
~  — для споживача обидва набори еквівалентні.
— для споживача обидва набори еквівалентні.
Переваги споживача можна подати у формі індикатора переваг, тобто такої функції корисності
 ,
,  ,
,
що з 
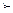
 випливає
випливає  ,
,
з 

 випливає
випливає  ,
,
з  ~
~  випливає
випливає  .
.
Уведення функції корисності дозволяє замінити відношення переваги звичними відношеннями між числами: більше, менше, дорівнює.
У теорії споживання припускаються гіпотези і вважається, що функція корисності неперерва та диференційована. Вона має такі властивості:
1)  — зі зростанням споживання товару корисність зростає;
— зі зростанням споживання товару корисність зростає;
2)  - зі зростанням споживання товару швидкість зростання корисності зменшується (спадає);
- зі зростанням споживання товару швидкість зростання корисності зменшується (спадає);
Розглянемо види функції корисності для товарів двох видів:
1) неокласична
 ,
,
2) із взаємозаміщенням
 ,
,
3) із взаємодоповненям
 ,
,
4) логарифмічна
 .
.
Розглянемо функцію корисності для товарів n видів
 .
.
Гранична корисність товару
 ,
,
показує, на скільки зростає корисність, якщо кількість товару зростає в малому обсязі.
Гранична норма заміщення товарів показує, скільки необхідно одиниць j-го товару, щоб замінити малий обсяг і-го товару, який вибув.
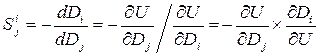 .
.
Припустимо, що функція корисності маї вигляд
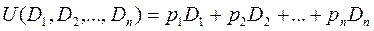 ,
,
де рi – ціна одиниці товару і-го виду, 
 .
.
Знайдемо граничні корисності
 ,
,  .
.
Розглянемо відношення граничних корисностей
 .
.
Це відношення має назву 2-го закону Госсена.
Тема 4
Моделювання поведінки споживачів
План
4.1 Модель поведінки споживача
4.2 Рівняння Є.Є. Слуцького
4.1 Змістовна постановка задачі споживача має вигляд.
Споживач має суму грошей і хоче її витратити з найбільшою користю для себе. Назвемо наявну суму грошей доходом споживача. Необхідно визначити, яку кількість товарів різних видів може придбати споживач на свій доход.
Математичну постановку задачі споживача можна сформулювати в такий спосіб.
Споживач хоче придбати набір товарів n видів

де Di – кількість товару i-го виду, 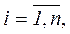

щоб максимізувати свою функцію корисності 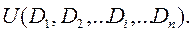 Відомі ціни товарів
Відомі ціни товарів

де рi – ціна одиниці товару і-го виду, 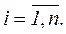
Вартість товарів, що купуються, не може перевищувати доход 
 .
.
Сформульовану постановку можна записати так


Припускаємо, що функція  безперервна та диференційована.
безперервна та диференційована.
Для рішення задачі споживача можна використати функції Лагранжа або другий закон Госсена. Розглянемоаємо функцію Лагранжа

де  - множник Лагранжа.
- множник Лагранжа.
Беремо перші похідні

Прирівнюємо похідні нулеві
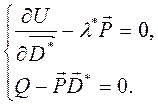
Перепишемо останній вираз у вигляді

Таким чином, одержуємо єдине рішення
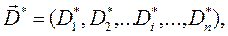
де  - функція попиту на товар і – го вигляду,
- функція попиту на товар і – го вигляду, 
4.2 Рівняння Слуцького виведене в 1915 році вченим Є.Є Слуцьким.
Рівняння Слуцького має вигляд і показує зміну попиту на споживчий товар при зміні його ціни, але з компенсацією доходу, що дозволяє залишитися на тім же рівні корисності:

 ,
, 
Тут 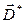 - вектор-функція попиту на товари,
- вектор-функція попиту на товари,
 - ціна і-го товару,
- ціна і-го товару, 
 - доход споживача,
- доход споживача,
 - попит на товар і-го виду,
- попит на товар і-го виду, 
Тема 5 
5 Моделі взаємодії споживачів та виробників
План
5.1 Рівновага на ринку одного товару
5.2 Павутиноподібна модель ринку
5.3 Модель Еванса
5.1 Стан ринку, при якому попит дорівнює пропозиції, називається рівнозваженим, а ціна при якій досягається рівність попиту та пропозиції, називається рівнозваженою ціною p*.
Знайдемо стан рівноваги для лінійних функцій попиту
D(p*  ) = a-bp*,
) = a-bp*,
і пропозиції
S(p*)= -c+dp*.
a - bp*=- c +dp*,
p* =  .
.
5.2 У реальності визначення рівнозваженої ціни відбувається досвідченим шляхом. Ця процедура називається павутиноподібною моделлю ринку.
Процес відшукання рівнозваженої ціни називається «намацуванням» і є ітераційним (рис.5.1). Припустимо що в початковий момент на ринку спостерігалася нестача товарів, ціна товару дорівнювала р0. У цих умовах виробник зацікавлений у збільшенні обсягу товару й у наступний момент викине на ринок товар в більшому обсязі, але за ціною р1,  . З огляду на знову сформовану ситуацію виробник товару в наступний момент викине на ринок товар у меншому обсязі. Ціна зміниться з p
. З огляду на знову сформовану ситуацію виробник товару в наступний момент викине на ринок товар у меншому обсязі. Ціна зміниться з p  до p
до p  , p
, p  < p1. Тобто одержуємо безперервне коливання навколо рівнозваженої ціни.
< p1. Тобто одержуємо безперервне коливання навколо рівнозваженої ціни.

Рис. 5.1
Якщо в деякому околу рівнозваженої ціни процес ітерацій сходиться до стану рівноваги при будь-якому початковому значенні ціни з цього околу, то стан рівноваги називається стійким. У противному випадку стан рівноваги називається нестійким.
На рис. 5.2 показана графічна модель, у якій стан рівноваги стійкий, а ціна змінюється від найменшої ціни (ціни покупя) до найбільшої ціни (ціни торговця). Для того, щоб стан рівноваги був стійким у цій моделі, необхідно виконання умови:
 ,
,
де  - похідна функції пропозиції,
- похідна функції пропозиції,
 - похідна функції попиту.
- похідна функції попиту.
Для аналітичного визначення рівнозваженої ціни зручно використати табл. 5.1.
Таблиця 5.1
| p | p0 | p1 | p2 | …………. | pn |
| D(p) | D0 | D1 | D2 | …………. | Dn |
| S(p) | S0 | 
| 
| …………. | 
|
В таблиці задається початкова ціна p0 ,  , а потім обчислюються D0 , S0
, а потім обчислюються D0 , S0
D0 = a-bp0,
S0= -c+dp0.
Із рис. 5.2 видно, що  . Звідси знаходимо нову ціну p1
. Звідси знаходимо нову ціну p1
S1= -c+dp1,
 .
.
Цю ціну наносимо в таблицю 5.1 і знаходимо D1 . Аналогічно обчислюємо інші значення цін, попиту та пропозиції. Ітераційний процес вкючає чотири-пять ітерацій.

На рис. 5.3 показана графічна модель, у якій стан рівноваги стійкий, а ціна змінюється від найбільшої ціни (ціни торговця) до найменшої ціни (ціни покупця) Для того, щоб стан рівноваги був стійким у цій моделі, необхідно виконання умови:
 .
.
Для аналітичного визначення рівнозваженої ціни зручно використати табл. 5.2.
Таблиця 5.2
| p | p0 | p1 | p2 | …………. | pn |
| D(p) | D0 | 
| 
| 
| |
| S(p) | S0 | S1 | S2 | …………. | Sn |
В таблиці задається початкова ціна p0 ,  , а потім обчислюються D0 , S0
, а потім обчислюються D0 , S0
D0 = a-bp0,
S0= -c+dp0.
Із рис. 5.3 видно, що  . Звідси знаходимо нову ціну p1
. Звідси знаходимо нову ціну p1
D1 = a-bp1,
 .
.
Цю ціну наносимо в таблицю 5.2 і знаходимо S1 . Аналогічно обчислюємо інші значення цін, попиту та пропозиції. Ітераційний процес вкючає чотири-пять ітерацій.
При побудові моделі, у якій стан рівноваги нестійкий, обчислення виконуються до одержання першого негативного значення ціни, попиту або пропозиції.
5.3 У моделі Еванса розглядається ринок одного товару, час вважається безперервним. Нехай d(t), s(t), p(t) - відповідно попит, пропозиція та ціна цього товару в момент t . Попит і пропозиція вважаються лінійними функціями ціни
d(p) = а - bp,(a, b) > 0,
тобто попит з ростом ціни падає,
s(p) =  +βp,
+βp,  < 0, β > 0,
< 0, β > 0,
тобто пропозиція з ростом ціни росте. Природно вважати, що a > 0, тобто при нульовій ціні попит є (по-іншому говорячи, товар бажаний).
Основне припущення складається у тім, що ціна змінюється в залежності від співвідношень між попитом та пропозицією:
∆p = y(d-s) ∆t, y > 0,
тобто збільшення ціни прямо пропорційно перевищенню попиту над пропозицією і тривалості цього перевищення.
Отже, одержуємо диференціальне рівняння
dp/dt = y(d - s).
Підставляючи в це рівняння лінійні залежності попиту та пропозиції від ціни, одержуємо лінійне неоднорідне диференціальне рівняння з початковою умовою:
dp/dt=-γ[(b+ β)p-(а-  )], p(0)=p0, (5.1)
)], p(0)=p0, (5.1)
Видно, що dp/dt > 0 при р* > р і dp/dt < 0 при р* < р. При цьому при
р* > р ціна прагне до р* зростаючи, а при р* > р — убуваючи. Сама ціна р* єрівнозваженою ціною — при ній рівні попит та пропозиція:
р  = (а-
= (а-  )/(b + β).
)/(b + β).
Рівнозважена ціна може бути знайдена також графічно як точка перетинання прямих попиту d(p) = a-bp і пропозиції s(p) =  + βр (рис. 5.4).
+ βр (рис. 5.4).
Звичайний метод рішення рівняння (5.1) - метод варіації постійної. Відповідно до цього методу загальне рішення є сума загального рішення відповідного однорідного рівняння dp/dt = -у(b + β)p і якого-небудь часткового рішення неоднорідного рівняння
р(t) = poe  +[( а-а)/(b+β)][l-e-
+[( а-а)/(b+β)][l-e-  ],
],
або
р(t) = poe  +p
+p  [1-e-
[1-e-  ].
].
Розглянемо дискретний аналог моделі Еванса. У дискретній моделі ринок функціонує в такий спосіб : ранком на ринку виявляються деякі пропозиція  і попит
і попит  . У залежності від їхніх значень ціна починає рівномірно рости або убувати: якщо ранком попит був більше пропозиції, то зростати, якщо пропозиція була більше попиту, то убувати.
. У залежності від їхніх значень ціна починає рівномірно рости або убувати: якщо ранком попит був більше пропозиції, то зростати, якщо пропозиція була більше попиту, то убувати.

Рис. 5.4
Припустимо, що початкова ціна була  , при цьому
, при цьому  . Отже, ціна почне зростати За день вона зросте до деякого значення
. Отже, ціна почне зростати За день вона зросте до деякого значення  , при цьому знову буде
, при цьому знову буде  і ціна буде зростати далі і далі, доки не досягне
і ціна буде зростати далі і далі, доки не досягне  .
.
Тема 6
Виробничі функції та ЇХ властивості
План
6.1 Види виробничих функці
6.2 Граничний аналіз факторів
6.3 Однорідність виробничих функцій
6.4 Еластичність виробничих функцій
6.5 Заміщення факторів у виробничих функціях
6.6 Виробнича функція Кобба-Дугласа
6.1 Виробничі функції можна розділити по кількості використовуваних перемінних, по вигляду функцій і по їхніх властивостях.
Під виробничою функцією розуміють економіко-математичне рівняння, що зв'язує випуск продукції і витрати ресурсів на цей випуск. Виробничі функції по кількості факторів розрізняють:
- однофакторні:  або
або 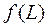 , де
, де  - обсяг ОВФ у натуральному або вартісному вигляді за конкретний період часу,
- обсяг ОВФ у натуральному або вартісному вигляді за конкретний період часу, 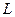 - кількість трудових ресурсів (середньосписочне число робітників, число людино-днів, тощо) за конкретний період часу,
- кількість трудових ресурсів (середньосписочне число робітників, число людино-днів, тощо) за конкретний період часу,
- двофакторні:  ;
;
- багатофакторні  , де t - фактор часу, r - індекс науково-технічного прогресу.
, де t - фактор часу, r - індекс науково-технічного прогресу.
По аналітичному вигляду розрізняють виробничі функції:
1) лінійні виробничі функції
 .
.
Тут  - обсяг випуску продукції у вартісному або натуральному вигляді за конкретний період часу.
- обсяг випуску продукції у вартісному або натуральному вигляді за конкретний період часу.
Параметри  і
і  виражають продуктивність факторів
виражають продуктивність факторів  і
і 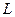 , тобто показують абсолютний приріст виробництва, коли один фактор залишається незмінним, а інший зростає на одиницю. Лінійні функції часто використовуються в короткостроковій і середньостроковій економічній моделях.
, тобто показують абсолютний приріст виробництва, коли один фактор залишається незмінним, а інший зростає на одиницю. Лінійні функції часто використовуються в короткостроковій і середньостроковій економічній моделях.
2) степеневі виробничі функції
 ,
,
 ,
,
Параметри  і
і  виражають еластичність рівня виробництва Х стосовно факторів
виражають еластичність рівня виробництва Х стосовно факторів  і
і 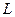 , тобто показують відносний приріст продукції, зв'язаний з відносним приростом
, тобто показують відносний приріст продукції, зв'язаний з відносним приростом  і
і 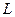 .
.
3) складні виробничі функції (CES)
 ,
,
де  - параметр, що виражає еластичність заміни ОВФ і трудових ресурсів.
- параметр, що виражає еластичність заміни ОВФ і трудових ресурсів.
6.2 Передбачається, що виробничі фактори задовольняють аксіомі.
Існує підмножина простору витрат, називана економічною областю М, у якій збільшення витрат будь-якого витрат не приводить до зменшення випуску продукції. Якщо  - дві точки цієї області, то
- дві точки цієї області, то  приводить до
приводить до  .
.
Ця аксіома затверджує, що виробничі фактори не якась зовсім абстрактна функція, придумана теоретиками - математиками. Вона відбиває твердження, нехай і не на усій своїй області визначення, а тільки на її частині: у мало-мальськи розумній економіці збільшення витрат не може привести до зменшення випуску продукції. У диференціальній формі це виражається в тім, що в цій області перші часткові похідні функції ненегативні.
Розглянемо виробничу функцію
 .
.
Нехай ця функція безперервна та диференційована
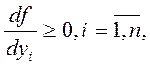
ці похідні називаються граничними продуктами.
Можна скласти виробничі функції даного виробництва навіть нічого не знаючи про виробництво. Треба тільки поставити на виробництві лічильник (людину або прилад), що буде фіксувати ресурси та кількість продукції, що на виробництві зроблено. Якщо нагромадити досить багато такої статистичної інформації, врахувати роботу виробництва в різних режимах, то можна прогнозувати випуск продукції, знаючи обсяг ресурсів, а це і є виробнича функція.
6.3 Поняття «однорідність виробничої функції» містить у собі наступна її властивість: рівномірне збільшення усіх виробничих факторів викликає пропорційне збільшення продукції. Виразимо цю властивість математично:
функція  однорідна в ступені h. якщо
однорідна в ступені h. якщо
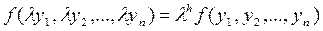 ,
,
де (  , h)>0.
, h)>0.
Таким чином, коли кожна незалежна змінна приймає значення  , значення функції
, значення функції 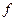 зростає в
зростає в  раз.
раз.
 Величина
Величина  показує ступінь використання виробничих факторів або їхню ефективність. У випадку, коли
показує ступінь використання виробничих факторів або їхню ефективність. У випадку, коли  , ефективність виробничих факторів дорівнює 1, при
, ефективність виробничих факторів дорівнює 1, при 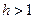 говорять, що виробничі фактори мають зростаючу ефективність і відповідно при
говорять, що виробничі фактори мають зростаючу ефективність і відповідно при 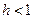 ефективність факторів знижується (рис. 6.1).
ефективність факторів знижується (рис. 6.1).
Рис. 6.1
6.4 Еластичністю економічного показника називається його здатність реагувати в більшому або меншому ступені на зміну іншого показника.
Визначимо еластичність обсягу виробництва  по деякому факторі. Розрахуємо частковий коефіцієнт еластичності Х за основними фондами
по деякому факторі. Розрахуємо частковий коефіцієнт еластичності Х за основними фондами  :
:
 .
.
Тут  безперервна та диференційована функція по
безперервна та диференційована функція по  та L.
та L.
Тому що на практиці ця умова виконується рідко, то часто коефіцієнт еластичності виражається через прирости. В дискретній формі частковий коефіцієнт еластичності  виражається формулою:
виражається формулою:
 .
.
Частковий коефіцієнт еластичності Х за трудовими ресурсами L дорівнює:
 .
.
В дискретній формі частковий коефіцієнт еластичності  виражається формулою:
виражається формулою:
 .
.
Частковий коефіцієнт еластичності показує на скільки відсотків зміниться обсяг випуску продукції, якщо відповідний виробничий фактор зміниться на один відсоток.
Для функції  параметри
параметри  і
і  є частковими коефіцієнтами еластичності
є частковими коефіцієнтами еластичності
 ,
,  .
.
Припустимо, що кожен виробничий фактор виріс на  %, тоді значення цих факторів дорівнюють:
%, тоді значення цих факторів дорівнюють:
 ;
;  .
.
Величина кінцевого продукту обчислюється за формулою:

При  кінцевий продукт зростає більше чим на r%, при
кінцевий продукт зростає більше чим на r%, при  - менше, ніж на
- менше, ніж на  %, а при
%, а при  - на
- на  %.
%.
6.5 Поняття заміщення ґрунтується на припущенні, що виробничі фактори можуть заміняти один одного, і показує, як при незмінній величині продукції можна змінювати співвідношення між факторами. Для 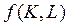 можна порушити питання, як має змінитися кількість трудових ресурсів при деякій зміні обсягу ОВФ, щоб величина зробленого продукту залишилася незмінною. Оцінка заміщення
можна порушити питання, як має змінитися кількість трудових ресурсів при деякій зміні обсягу ОВФ, щоб величина зробленого продукту залишилася незмінною. Оцінка заміщення  і
і 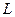 визначається як відношення двох граничних величин і називається граничною нормою заміщення
визначається як відношення двох граничних величин і називається граничною нормою заміщення

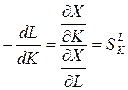 .
.
Розрізняють виробничі функції із взаємозамінними факторами (рис. 6.4, а) та із факторами, що доповнюють (рис. 6.4, б).

а) б)
Рис.6.4
На рисунку 6.4 зображені ізокванти виробничих функцій. Кожна точка показує значення продукту, одержаного за допомогою комбінації факторів  . Безліч цих точок лежить на поверхні, називаною поверхнею виробничих функцій. Перетинання цієї поверхні з площинами, рівнобіжними площинам
. Безліч цих точок лежить на поверхні, називаною поверхнею виробничих функцій. Перетинання цієї поверхні з площинами, рівнобіжними площинам  , утворять криві, називані ізоквантами. Кожна точка на цих кривих дає комбінацію виробничих факторів, що відповідають однаковому значенню виробничих функцій.
, утворять криві, називані ізоквантами. Кожна точка на цих кривих дає комбінацію виробничих факторів, що відповідають однаковому значенню виробничих функцій.
Якщо виробничі фактори можна заміняти лише у фіксованих пропорціях, то говорять, що виробничі функції володіють нульовою граничною нормою заміщення.
6.6 Виробнича функція Кобба-Дугласа (CDPF) належить до найбільш відомих, широко застосовуваних функцій
 ,
,
(a,α,(1-α))>0, α<1.
Вчені Кобб і Дуглас зробили спробу оцінити значення  степенової виробничої функції
степенової виробничої функції
 ,
,  ,
,
використовуючи дані по американській обробній промисловості за період з 1899 по 1922 роки – індекс виробництва Х, індекс основного капіталу  , індекс праці
, індекс праці 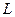 . Вони прийшли до висновку, що
. Вони прийшли до висновку, що
 ,
,
(у такий спосіб має місце незмінний ефект масштабу). З тих пір формула
 ,
,
 ,
,
для якої  називають функцією Кобба-Дугласа.
називають функцією Кобба-Дугласа.
З часом функція перетерпіла зміни
 ,
,
де  - темп науково-технічного прогресу,
- темп науково-технічного прогресу,
t – час.
При 
 .
.
Знайдемо тепер часткові коефіцієнти еластичності продукції за основними фондами
 ,
,
та за трудовими ресурсами

Прологарифмуємо CDPF
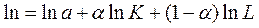 .
.
Тепер виробнича функція Кобба-Дугласа має лінійний вигляд.
При збільшенні кожного виробничого фактора на m відсотків обсяг випуск упродукції також збільшується на m відсотків
 ,
,
Знайдемо граничні норми заміщення основними фондами трудових ресурсів по формулі:
 .
.
а трудовими ресурсами основних фондів по формулі:
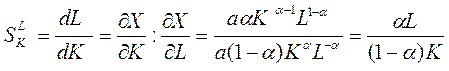 .
.
Тема 7
Моделювання поведінки виробників
План
7.1 Моделі поведінки виробника
7.2 Умови роботи двох фірм на ринку одного товару
7.1 Розглянемо математичну постановку задачі виробника.
Фірма випускає продукцію одного виду. Обсяг продукції, який випускається за конкретний період часу (наприклад, за рік, місяць тощо) позначимо Y. Обсяг продукції фірми визначається виробничою функцією. Передбачається, що ця функція безперервна та диференційована

де  - обсяг витрат ресурсів або виробничих факторів.
- обсяг витрат ресурсів або виробничих факторів.
До виробничих факторів можуть бути віднесені: основні виробничі фонди, трудові ресурси (середня чисельність зайнятих людей або відпрацьованих людино-днів за конкретний період часу), витрачені за цей проміжок часу матеріали, сировина, енергія тощо.
Нехай  – вектор – рядок цін ресурсів, а p – ціна продукції. Тоді прибуток фірми дорівнює
– вектор – рядок цін ресурсів, а p – ціна продукції. Тоді прибуток фірми дорівнює

Тут  - доход фірми при випуску розглянутої продукції,
- доход фірми при випуску розглянутої продукції,  - вартість витрат ресурсів за конкретний період часу.
- вартість витрат ресурсів за конкретний період часу.
Задача максимізації прибутку має вигляд

Для пошуку оптимальних значень вектору  необхідно розглянути перші похідні
необхідно розглянути перші похідні

Цей вираз можна переписати таким чином


Прирівнюємо перші похідні нулеві

Перепишемо цей вираз у вигляді

Звідси

Тепер розглянемо модель, якщо фірма хоче максимізувати обсяг випуску продукції. До розглянутих умов додається така умова: відома вартість С витрат ресурсів за конкретний період часу, але невідома ціна одиниці продукції, що випускається. Цільову функцію та обмеження представимо у вигляді

Побудуємо функцію Лагранжа
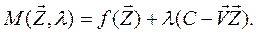
тут  – множник Лагранжа. Щоб максимізувати цю функцію необхідно розглянути перші похідні
– множник Лагранжа. Щоб максимізувати цю функцію необхідно розглянути перші похідні


Перепишемо останні рівняння у вигляді

Прирівнюємо ці похідні нулеві
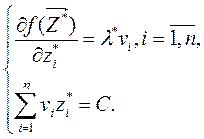
Вирішуючи цю систему, можна знайти оптимальні значення вектору 
7.2 Розглянемо ринок двох фірм, що випускають продукцію одного виду. Нехай собівартість випуску одиниці продукції дорівнює а. Зробленай обома фірмами продукція надходить на загальний ринок. Ціна на товар лінійно падає в залежності від загальної кількості товару, що надходить на ринок
x = x1+x2 ,
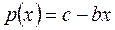 ,
, 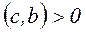 ,
,
де х1 – обсяг продукції першої фірми,
х2 - обсяг продукції другої фірми,
с - гранично висока (максимальна) ціна продукції,
b – коефіцієнт лінійної залежності.
Прибуток першої фірми можна визначити по формулі:
 ,
,
де  .
.
Прибуток другої фірми можна визначити по формулі:
 .
.
Поведінка кожної фірми визначається її прагненням максимізувати вій прибуток. Допустимо, що перша фірма довідалася про стратегію другої фірми, тобто про її обсяг випуску продукції. Тоді перша фірма вибирає свій випуск з умови максимізації свого прибутку:

 ,
,

Друга фірма також вибирає свій випуск з умови максимізації свого прибутку:
 ,
,
 ,
,  .
.
Тема 8
Моделювання співробітництва та конкуренції фірм
План
8.1 Стратегія Курно
8.2 Стратегія Стакельберга
8.3 Стратегія монополії
8.4 Стратегія картелю
8.1 Стратегія кожного підприємства визначається її прагненням максимізувати свій прибуток.
Відповідно стратегії Курно, припускаємо, що виробничі цикли підприємств збігаються. Тоді підприємства вибирають свої оптимальні випуски, знаючи обсяг виробництва свого конкурента за минулий або поточний періоди. Нехай  .
.
Обсяг випуску за попередній період дорівнює:
 . .
|
Обсяг випуску за нинішній період дорівнює:
 . .
|
На підставі (2.8) і (2.9) знайдемо х1 і х2.
 . .
|
Обсяг випуску продукції другого підприємства дорівнює:
 . .
|
Ціна продукції визначається по формулі:
р(х) = с – bх = с -  . .
|
Прибуток підприємств дорівнює:
 , ,
 . .
|
Загальний прибуток двох підприємств:
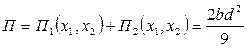 . .
|

Рисунок 8.1
8.2 Відповідно стратегії Стакельберга, припускаємо, що одне з підприємств свідомо розкриє свою стратегію. Нехай перше підприємство дасть можливість другому підприємству довідатися свій обсяг х1, тоді друге підприємство випустить продукцію в обсязі:  . Перше підприємство буде тепер діяти, виходячи саме з такої стратегії другого підприємства. Знайдемо прибуток першого підприємства:
. Перше підприємство буде тепер діяти, виходячи саме з такої стратегії другого підприємства. Знайдемо прибуток першого підприємства:
 . .
|
З огляду на, що  знаходимо.
знаходимо.  .
.
Ціна продукції дорівнює:
р(х) = с – bх = с -  . .
|
Прибуток двох підприємств відповідно:
 , ,
 . .
|
Сумарний прибуток:
 . .
|
8.3 В умовах співробітництва двох підприємств можливе утворення монополії, що поєднує обоє підприємства в одне, і картелю, по суті являющегося таємною змовою двох учасників ринку з метою максимізації прибутку. Для монополії загальний прибуток буде дорівнює bd2/4, а для картелю в загальному випадку прибуток кожного учасника буде рівної bd2/8 при рівних обсягах випуску продукції
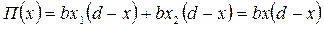 , ,
 , ,
 . .
|
8.4 Картель – таємна змова декількох фірм із метою підтримки заданої ціни. Припустимо, що антимонопольне законодавство забороняє злиття двох фірм – утворення монополії .
Тому ці фірми використовують попередні розрахунки .кожна фірма буде випускати  одиниць товару прибуток дорівнює
одиниць товару прибуток дорівнює  ;
;  ;
;
Результати розрахунків оформимо у виді табл.
| Стратегія | х1 | х2 | х | П1 | П2 | П | р |
| Курно | 
| 
| 
| 
| 
| 
| 
|
| Стакельберга | 
| 
| 
| 
| 
| 
| 
|
| монополії | 
| 
| 
| ||||
| картелю | 
| 
| 
| 
| 
| 
| 
|
Висновки:
1) Для споживача найбільш краща крапка Стакельберга, у якій ціна товару min а обсяг випуску max .
2) Для споживача менш усього сприятливо ситуація монополії або Картелю, де ціна max , а випуск товару min ,а сумарний прибуток – max .
Тема 9
Рейтингове оцінювання та управління в економіці
План
9.1 Концепція рейтингового управління
9.2 Модель обчислення рейтингу економічної системи
9.1 Виявлення ключових аспектів щодо оцінювання стану та динаміки функціонування економічних систем стає однією з актуальних проблем в економічній практиці та науці. Важливою складовою цієї проблеми є аналіз стану досліджуваної економічної системи.
У зв’язку зі складністю одночасного контролю великої кількості різноманітних показників у фінансово-економічному аналізі значного поширення набули процедури комплексної оцінки, на підставі яких може обчислюватися рейтинг як узагальнена оцінка діяльності економічної системи (ЕС). Під рейтингом розуміють комплексну характеристику ЕС згідно з певною шкалою, де значення рейтингу — це елемент лінійно напівупорядкованої множини.
Рейтинг являє собою оцінку тих чи інших аспектів діяльності досліджуваної ЕС за фіксованої шкали. Отже, рейтинг є комплексною інформацією щодо стану ЕС, яка подається в максимально згорнутому вигляді.
На жаль, до цього часу використання рейтингу не привело до суттєвої трансформації процедур прийняття рішень користувачами рейтингової інформації (що передусім пов’язано з відірваністю існуючих методик рейтингового оцінювання від реальної схеми прийняття рішень користувачами).
Означення рейтингового управління, наведене нижче, має на меті змінити ситуацію, що склалася.
Рейтингове управління – концепція прийняття рішень потенційними користувачами на підставі використання рейтингів у процесі реалізації функцій управління.
Із цього означення випливає, що рейтингове управління є процесом, у якому рейтинг використовується для аналізу, контролю, обліку, прогнозування та регулювання діяльності ЕС. Тому методику обчислення рейтингу можна інтерпретувати як цільову функцію рейтингового управління, значення якої є індикатором стану ЕС.
9.2 Для визначення рейтингу ЕС можна використати метод аналізу ієрархій (МАІ). Цей метод є систематичною процедурою для ієрархічного представлення елементів, що визначають суть проблеми.
Метод складається в декомпозиції проблеми на усе більш прості складові частини і подальшій обробці послідовності суджень особи, що приймає рішення, по парних порівняннях. У результаті може бути виражений відносний ступінь (інтенсивність) взаємодії елементів в ієрархії. Ці судження потім виражаються чисельно. МАІ містить у собі процедури синтезу множинних суджень, одержання пріоритетності критеріїв і визначення альтернативних рішень. Такий підхід до рішення проблеми вибору виходить із природної здатності людей думати логічно і творчо, визначати події і встановлювати стосунки між ними.
Таким чином, у МАІ основна мета дослідження і усі фактори, у тім або іншому ступені, що впливають на досягнення мети, розподіляються по рівнях у залежності від ступеня і характеру впливу. На першому рівні ієрархії завжди знаходиться одна вершина – ціль проведеного дослідження.
Другий рівень ієрархії складають фактори, що безпосередньо впливають на досягнення мети. При цьому кожен фактор представляється в споруджуваній ієрархії вершиною, з'єднаною з вершиною першого рівня.
Третій рівень складають фактори, від яких залежать вершини другого рівня. І так далі. Цей процес побудови ієрархії продовжується до тих, поки в ієрархію не включені всі основні фактори або хоча б для одного з факторів останнього рівня неможливо безпосередньо одержати необхідну інформацію.
По закінченні побудови ієрархії для кожної материнської вершини проводиться оцінка вагових коефіцієнтів, що визначають ступінь її залежності від вершин, що впливають на неї, більш
Дата добавления: 2014-12-03; просмотров: 833; Мы поможем в написании вашей работы!; Нарушение авторских прав |