
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Импульс. Закон сохранения импульса.
В механической системе, состоящей из нескольких тел, существуют как силы взаимодействия между телами системы, которые называются внутренними, так и силы взаимодействия этих тел с телами, не входящими в данную систему, которые называются внешними. Если внешние силы отсутствуют, то механическая система называется замкнутой.
Для замкнутой механической системы существует несколько физических величин, которые остаются постоянными с течением времени. Одной из таких величин является импульс тела, который является вектором и равен произведению массы тела m на вектор скорости тела v : p = mv . Для механической системы ее импульс равен векторной сумме импульсов, составляющих ее n тел:

Пользуясь выражением для импульса и учитывая постоянство массы тела, представим второй закон Ньютона в следующем виде:
 (3.2)
(3.2)
Рассмотрим изолированную систему, состоящую из двух движущихся тел. Сталкиваясь друг с другом, тела (упругие шары) будут изменять свой импульс. Рассматривая взаимодействие тел в течение небольшого промежутка времени Dt и применяя к каждому телу закон изменения импульса, можно записать:


 ,
,  – результирующие силы, действующие на каждое тело,
– результирующие силы, действующие на каждое тело,
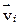 ,
, 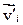 – скорости в начале и в конце рассматриваемого промежутка времени.
– скорости в начале и в конце рассматриваемого промежутка времени.
Складывая равенства почленно, получим:

 и
и  – силы внутренние, тогда по III закону Ньютона
– силы внутренние, тогда по III закону Ньютона  =-
=-  .
.
Тогда
 .
.
Это означает, что сумма импульсов обеих тел системы не изменяется со временем, т.е.  .
.
Введем величину 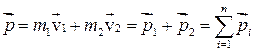 , представляющую вектор импульса всей системы (или полный импульс системы).
, представляющую вектор импульса всей системы (или полный импульс системы).
Тогда для системы из “n” тел
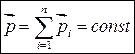 (3.3)
(3.3)
или из II закона Ньютона
 , (3.4)
, (3.4)
т.к. система замкнута.
Эти равенства выражают закон сохранения импульса.
ОПРЕДЕЛЕНИЕ: Полный вектор импульса замкнутой (или изолированной) системы тел с течением времени не изменяется.
Пусть теперь на тела A и B действуют теперь как внутренние, так и внешние силы: на тело A –  и
и  , а на тело B –
, а на тело B –  и
и  .
.
Тогда  ,
,
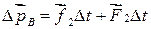
или, что равносильно для системы из “n” тел:  .
.
Складывая эти уравнения с учетом, что  , получаем
, получаем
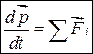 . (3.5)
. (3.5)
Следовательно, производная по времени от вектора импульса системы равна сумме всех внешних сил, приложенных к телам системы.
Для замкнутой системы  , вследствие чего полный импульс не зависит от времени. Это утверждение представляет собой содержание закона сохранения импульса. Повторим его:
, вследствие чего полный импульс не зависит от времени. Это утверждение представляет собой содержание закона сохранения импульса. Повторим его:
ОПРЕДЕЛЕНИЕ: Импульс замкнутой системы тел остается постоянным.
Отметим, что импульс системы тел остается постоянным и для системы, подверженной внешним воздействиям, при условии, что внешние силы, действующие на тела системы, в сумме дают нуль. Если даже сумма внешних сил не равна нулю, но проекция этой суммы на некоторое направление есть нуль, то составляющая импульса в этом направлении будет постоянной.
Дата добавления: 2014-12-03; просмотров: 317; Мы поможем в написании вашей работы!; Нарушение авторских прав |