Поступательное движение твердого тела.

ОПРЕДЕЛЕНИЕ: Абсолютно твердым телом будем называть такое тело, деформациями которого в условиях рассматриваемой задачи можно пренебречь.

или

Абсолютно твердым телом называется такое тело, у которого расстояние между его частями сохраняется неизменным за все время движения.

Всякое движение твердого тела можно разложить на два основных вида движения – поступательное и вращательное.

Рассмотрим первый из них.

ОПРЕДЕЛЕНИЕ: Поступательное движение – это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе (рис. 4.1).

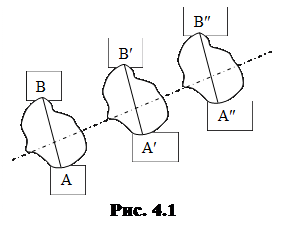При поступательном движении все точки тела получают за один и тот же промежуток времени равные по величине и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Наиболее простым видом поступательного движения является прямолинейное движение. В этом случае траектории всех точек тела – параллельные прямые.

Рассмотрим движение твердого тела, представив его как систему материальных точек с элементарной массой m_i. Каждая из этих элементарных масс может находиться под воздействием как внутренних сил , обусловленных ее взаимодействием с другими элементарными массами рассматриваемого тела, так и внешних сил .

Напишем для каждой элементарной массы II закон Ньютона:

,

где и – результирующие всех внутренних и внешних сил, приложенных к данной элементарной массе.

Складывая эти уравнения для всех элементарных масс, получим

.

Сумма всех внутренних сил , тогда имеем . Здесь – результирующая всех внешних сил, действующих на тело.

Рассмотрим теперь сумму, стоящую в левой части уравнения.

ОПРЕДЕЛЕНИЕ: Назовем центром инерции (центром масс) системы точку, положение которой в пространстве задается радиус-вектором , определяемым следующим образом: , где m_i – масса i-го тела, – радиус вектор, определяющий положение этого тела в пространстве, m – масса системы.

Продифференцируем дважды радиус-вектор центра инерции по времени и учитывая, что и , сумму в левой части можно записать в виде .

Следовательно,

– закон движения центра инерции твердого тела.

ОПРЕДЕЛЕНИЕ: Центр инерции твердого тела движется так, как двигалась бы материальная точка с массой равной массе тела, под действием всех приложенных к телу сил.

В случае поступательного движения это уравнение будет определять ускорение не только центра инерции, но любой другой точки тела.