
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение 4. Дополнительным или противоположным к событию А называется событие , означающее, что событие А не происходит.
Пусть 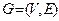 – неориентированный граф. Маршрутомв
– неориентированный граф. Маршрутомв  называется чередующаяся последовательность вершин и ребер
называется чередующаяся последовательность вершин и ребер 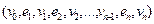 , такая, что ребра
, такая, что ребра 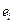 инцидентны вершинам
инцидентны вершинам  . Вершина
. Вершина 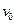 называется началом маршрута, а
называется началом маршрута, а  — концом. Одни и те же ребро и вершина могут встречаться в маршруте несколько раз. Будем называть маршрут цепью, если все его ребра различны. Цепь называется простой цепью, если все ее вершины, кроме, может быть,
— концом. Одни и те же ребро и вершина могут встречаться в маршруте несколько раз. Будем называть маршрут цепью, если все его ребра различны. Цепь называется простой цепью, если все ее вершины, кроме, может быть, 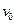 и
и  , различны. (В ряде руководств по теории графов принята другая терминология: то, что мы называем маршрутом, называется цепью, то, что мы называем цепью, — простой цепью и то, что мы называем простой цепью, - элементарной цепью). Число n называется длиной цепи. Цепь (простая цепь) называется циклом (соответственно простым циклом), если
, различны. (В ряде руководств по теории графов принята другая терминология: то, что мы называем маршрутом, называется цепью, то, что мы называем цепью, — простой цепью и то, что мы называем простой цепью, - элементарной цепью). Число n называется длиной цепи. Цепь (простая цепь) называется циклом (соответственно простым циклом), если 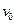 =
=  . Ниже, указывая маршрут в графе, будем обозначать его вершины и ребра так, как они в этом графе обозначены, не придерживаясь обозначений
. Ниже, указывая маршрут в графе, будем обозначать его вершины и ребра так, как они в этом графе обозначены, не придерживаясь обозначений 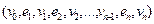 .
.
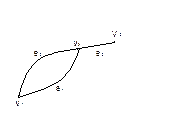 |
Примеры. 1. В следующем графе
последовательность 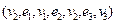 определяет маршрут с начало
определяет маршрут с начало  и концом
и концом 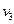 , являющийся цепью, но не простой цепью. Маршрут
, являющийся цепью, но не простой цепью. Маршрут 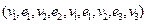 цепью не является.
цепью не является.
2. Как правило, маршрут в графе однозначно определяется последовательностью ребер, например, если любые два соседних ребра маршрута имеют только одну общую инцидентную вершину; вершина первого ребра, не инцидентная второму, является началом маршрута, а вершина последнего ребра, не инцидентная предпоследнему, - концом. Пользуясь этим замечанием, рассмотрим маршруты в следующем графе:
 |
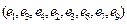 – маршрут, не являющийся цепью, с началом
– маршрут, не являющийся цепью, с началом 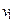 и концом
и концом 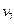 ;
;
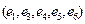 - цепь, не являющаяся простой цепью;
- цепь, не являющаяся простой цепью;
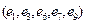 – простая цепь;
– простая цепь;
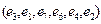 – цикл, не являющийся простым циклом;
– цикл, не являющийся простым циклом;
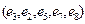 – простой цикл.
– простой цикл.
Вершины  и
и 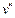 называются связанными, если существует маршрут в графе с началом в
называются связанными, если существует маршрут в графе с началом в  и концом в
и концом в 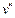 . Легко видеть, что в этом случае существует и простая цепь с началом в
. Легко видеть, что в этом случае существует и простая цепь с началом в  и концом
и концом 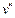 : в самом деле, если какая-нибудь вершина
: в самом деле, если какая-нибудь вершина 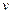 встречается несколько раз в последовательности, задающей маршрут, то, выбросив из последовательности все вершины и ребра между первым и последним появлением
встречается несколько раз в последовательности, задающей маршрут, то, выбросив из последовательности все вершины и ребра между первым и последним появлением 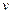 , мы получим маршрут, в котором
, мы получим маршрут, в котором 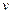 встречается только один раз; повторив нужное число раз эту процедуру, получим искомую простую цепь.
встречается только один раз; повторив нужное число раз эту процедуру, получим искомую простую цепь.
Рассмотрим бинарное отношение R на множестве вершин графа: 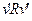 , если
, если  и
и 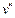 — связанные вершины. Читателю предоставляется проверить, что это отношение является отношением эквивалентности. Следовательно, возникает разбиение множества вершин графа на классы эквивалентности: две вершины относятся к одному классу эквивалентности, если они являются связанными. Далее, рассмотрим один из классов эквивалентности вместе с множеством всех ребер, инцидентных вершинам из этого класса. Мы получим подграф данного графа, называемый компонентой связности. Граф, состоящий из одной компоненты связности, называется связным. (Можно сказать проще: граф связен, если любые две его вершины являются связанными).
— связанные вершины. Читателю предоставляется проверить, что это отношение является отношением эквивалентности. Следовательно, возникает разбиение множества вершин графа на классы эквивалентности: две вершины относятся к одному классу эквивалентности, если они являются связанными. Далее, рассмотрим один из классов эквивалентности вместе с множеством всех ребер, инцидентных вершинам из этого класса. Мы получим подграф данного графа, называемый компонентой связности. Граф, состоящий из одной компоненты связности, называется связным. (Можно сказать проще: граф связен, если любые две его вершины являются связанными).
 |
Пример графа с двумя компонентами связности:
В графе можно удалять ребра и вершины. Если удаляется ребро, то все вершины сохраняются, если же удаляется вершина, то удаляются все инцидентные ей ребра. Вершина, при удалении которой число компонент связности увеличивается, называется точкой сочленения. Ребро с таким свойством называется мостом.
Рассмотрим связный граф. Для любых двух его вершин существует связывающий их маршрут, который можно считать простой цепью. Эта простая цепь не единственна. Минимальная длина простой цепи, связывающей две вершины  и
и 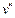 связного графа, называется расстоянием между вершинами и обозначается
связного графа, называется расстоянием между вершинами и обозначается  .
.
Легко проверить, что  обладает всеми свойствами расстояния (или метрики), определяемой на произвольном множестве, а именно:
обладает всеми свойствами расстояния (или метрики), определяемой на произвольном множестве, а именно:
1) 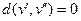 тогда и только тогда, когда
тогда и только тогда, когда 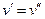 ;
;
2) 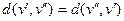 ;
;
3) 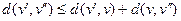 (неравенство треугольника).
(неравенство треугольника).
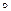 Для проверки последнего свойства положим
Для проверки последнего свойства положим  ,
, 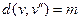 и рассмотрим простые цепи
и рассмотрим простые цепи 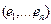 и
и 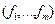 , на которых достигаются
, на которых достигаются  и
и 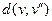 соответственно. Маршрут
соответственно. Маршрут 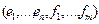 , очевидно, связывает
, очевидно, связывает  с
с 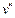 . Ясно, что
. Ясно, что  не больше, чем число ребер в этом маршруте, то есть чем
не больше, чем число ребер в этом маршруте, то есть чем 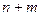 .
. 
С расстоянием между вершинами связаны понятия радиуса, диаметра и центра графа. Дадим нужные определения.
Максимальное расстояние между двумя вершинами графа G называется диаметром графа и обозначается  . Кратчайшие простые цепи, связывающие вершины с максимальным расстоянием между ними, называются диаметральными цепями.
. Кратчайшие простые цепи, связывающие вершины с максимальным расстоянием между ними, называются диаметральными цепями.
Максимальным удалением от вершины 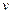 называется величина
называется величина 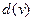 , равная максимальному расстоянию от
, равная максимальному расстоянию от 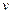 до других вершин графа.
до других вершин графа.
Вершина, максимальное удаление от которой минимально, называется центромграфа, а значение максимального удаления от центра называется радиусом графа и обозначается  . Отметим, что центр не единственен. Так, в полном графе
. Отметим, что центр не единственен. Так, в полном графе 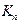 ( в котором любые две вершины соединены единственным ребром) центром является любая вершина, а радиус и диаметр равны единице.
( в котором любые две вершины соединены единственным ребром) центром является любая вершина, а радиус и диаметр равны единице.
Пример.
Проверьте, что в следующем графе:
1)  ;
;
2) 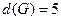 ;
;
3) 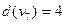 ;
;
4) 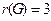 , центры:
, центры: 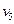 ,
, 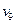 .
.
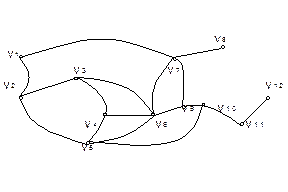 |
Определение максимального удаления и центра графа имеет важное практическое значение при размещении станций скорой помощи, отделений милиции, пожарных частей и других аварийных служб и пунктов обслуживания. С такого рода задачами часто связаны задачи о кратчайших маршрутах.
Определение 4. Дополнительным или противоположным к событию А называется событие , означающее, что событие А не происходит.

Свойства вероятности.
Теорема (сложения вероятностей несовместных событий). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Следствие 1: Если события  образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

Теорема (сложения вероятностей совместных событий). Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Следствие 2: Сумма вероятностей противоположных событий равна единице.

Определение 1. Событие А называется независимым от события В, вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Определение 2. Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В.

Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

Также можно записать: 
Если события независимые, то  , и теорема умножения вероятностей принимает вид:
, и теорема умножения вероятностей принимает вид:

Вероятность появления хотя бы одного события.
Если в результате испытания может появиться п событий, независимых в совокупности, то вероятность появления хотя бы одного из них равна

Здесь событие А обозначает наступление хотя бы одного из событий Ai, а qi – вероятность противоположных событий  .
.
Пример. Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,9; третий – 0,8. Найти вероятность того, что студентом будут сданы :
1) только 2-ой экзамен - событие А;
2) только один экзамен – событие В;
3) три экзамена – событие С;
4) хотя бы один экзамен – событие D.
5) не здаст ни один экзамен – событие Е;
Решение.
Обозначим р1=0,9 , тогда q1=0,1 т.к 
p2=0,9 q2=0,1
p3=0,8 q3=0,2
1) 
2) 
3) 
4) 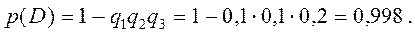
5) 
Основные формулы вычисления вероятностей
Формула полной вероятности.
Пусть некоторое событие А может произойти вместе с одним из несовместных событий  , составляющих полную группу событий. Пусть известны вероятности этих событий
, составляющих полную группу событий. Пусть известны вероятности этих событий  и условные вероятности наступления события А при наступлении события Hi
и условные вероятности наступления события А при наступлении события Hi 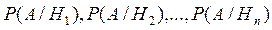 .
.
Теорема. Вероятность события А, которое может произойти вместе с одним из событий  , равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.
, равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.

Формула Бейеса. (формула гипотез)
Пусть имеется полная группа несовместных гипотез 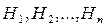 с известными вероятностями их наступления
с известными вероятностями их наступления  . Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности
. Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности 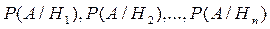 .
.
Требуется определить какие вероятности имеют гипотезы  относительно события А, т.е. условные вероятности
относительно события А, т.е. условные вероятности  .
.
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.

Эта формула называется формулой Бейеса.
Повторение испытаний.
Формула Бернулли.
Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.
Допустим, что событие А наступает в каждом испытании с вероятностью Р(А)=р. Вероятность Рт,п того, что в результате п испытаний событие А наступило ровно т раз равно
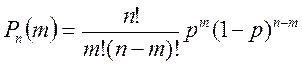 формула Бернулли.
формула Бернулли.





Случайные величины
Определение 1. Случайной величинойназывается величина, которая в результате опыта может прининять любое значение, причем заранее неизвестное.
Случайные величины можно разделить на две категории.
Определение 2. Дискретной случайной величиной (ДСВ) называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы).
Это множество может быть как конечным, так и бесконечным.
Определение 3. Непрерывной случайной величиной (НСВ) называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.
Закон распределения дискретной случайной величины.
Определение 1. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретнойслучайной Закон распределения ДСВ можно задать в виде:
1) таблицы ( ряд распределения)

Проверка: 
2) аналитически ( в виде интегральной функции F(x))

Функцию распределения можно представить графически в виде ступенчатой функции

3) графически ( в виде многоугольника или полигона распределения)
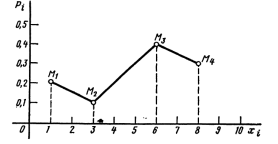
Числовые характеристики дискретных случайных величин.
Закон распределения полностью характеризует случайную величину. Однако, когда невозможно найти закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины. Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.
Определение 1. Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности. 
С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания.
1) 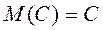
2) 
3) 
4)  , где Х и Y - две независимые сл. величины
, где Х и Y - две независимые сл. величины
Определение 2 . Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Свойства дисперсии.
1) 
2) 
3)  ,где Х и Y - две независимые сл. величины
,где Х и Y - две независимые сл. величины
4) 
Определение 3. Средним квадратическим отклонениемслучайной величины Х называется квадратный корень из дисперсии.

Пример 1. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно р1=0,3; p2=0,4; p3=0,5; p4=0,6. Найти математическое ожидание и дисперсию числа отказавших приборов.
Решение:
Принимая за случайную величину число отказавших приборов, видим что эта случайная величина может принимать значения 0, 1, 2, 3 или 4.
Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем  .
.
Т.к р1=0,3 , то q1=0,7
p2=0,4 q2=0,6
p3=0,5 q3=0,5
p4=0,6 q4=0,4
1) Не отказал ни один прибор.

2) Отказал один из приборов.
 0,302.
0,302.
3) Отказали два прибора.
 4) Отказали три прибора.
4) Отказали три прибора.

5) Отказали все приборы.

Получаем закон распределения:
| x | |||||
| p | 0,084 | 0,302 | 0,38 | 0,198 | 0,036 |
Проверка: 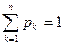
Математическое ожидание:


Дисперсия:

Пример 2. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятности числа попаданий и построить многоугольник распределения.
Вероятности по формуле Бернулли и равны соответственно:





 ,
,
| x | ||||||
| p | 0,0778 | 0,2592 | 0,3456 | 0,2304 | 0,0768 | 0,0102 |
Представим графически зависимость числа попаданий от их вероятностей.

Функция распределения.
Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. Х < x, обозначим через F(x).
Определение1. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.
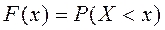
Функцию распределения также называют интегральной функцией.
Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.
Функция распределения дискретной случайной величины Х разрывна и возрастает скачками при переходе через каждое значение хi.
Свойства функции распределения..
1) 
2) F(x) – неубывающая функция.
3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна приращению функции распределения на этом интервале.

4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.
5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.
Плотность распределения.
Определение1. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).

Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
Свойства плотности распределения.
1) 
2) 
3)  .
.
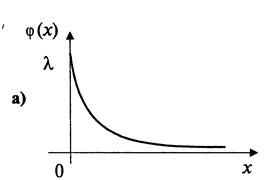
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b.
4) 
Числовые характеристики непрерывных случайных величин.
Пусть непрерывная случайная величина Х задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [a,b].
Определение1. Математическим ожиданиемнепрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл
 или
или 
Определение2 .Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.

По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

Определение 3. Средним квадратичным отклонениемназывается квадратный корень из дисперсии.
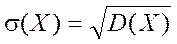































Дата добавления: 2014-12-03; просмотров: 298; Мы поможем в написании вашей работы!; Нарушение авторских прав |