
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Використання рівняння Шредінгера до атома водню. Хвильова функція. Квантові числа
Теорія Бора будови й властивостей енергетичних рівнів електронів у водневоподібних системах знайшла своє підтвердження у квантовій механіці. Квантова механіка також стверджує, що:
a) електрони в атомах водню знаходяться лише в дискретних енергетичних станах. При переході електронів з одних станів в інші випромінюється або поглинається фотон;
б) не існує певних колових орбіт електронів. В силу хвильової природи електрони «розмиті» в просторі подібно до хмарки негативного заряду. Розміри й форму такої хмарки в заданому стані можна розрахувати.
Розглянемо рух електрона в кулонівському полі ядра із зарядом Ze, потенціальна енергія якого виражається формулою
 , (1.4.1)
, (1.4.1)
де r – відстань між електроном і ядром.
Стан електрона в атомі водню або водневоподібному атомі описується деякою хвильовою функцією Y, яка задовольняє стаціонарне рівняння Шредінгера:
 , (1.4.2)
, (1.4.2)
де  ― оператор Лапласа; Е ― значення повної енергії електрона в атомі; m ― маса частинки;
― оператор Лапласа; Е ― значення повної енергії електрона в атомі; m ― маса частинки; 
 (x,y,z) ― хвильова функція у декартовій системі координат.
(x,y,z) ― хвильова функція у декартовій системі координат.
Для розв’язування рівняння Шредінгера (1.4.2), тобто знаходження виду хвильової функції для електрона в атомі водню слід перейти від декартових координат до сферичних. У цьому випадку зв’язок між параметрами цих систем координат визначається з рис. 1.12.
Співвідношення, які пов’язують координати x,y,z декартової прямокутної системи координат із сферичними координатами r, q, j такі:
 (1.4.3)
(1.4.3)

Рис. 1.12
Таким чином можна вважати, що хвильова функція y електрона в атомі водню залежить від сферичних координат, тобто y=y(r, q, j).
Опустивши досить громіздкі перетворення переходу від декартової системи координат до сферичної, одержимо:
 . (1.4.4)
. (1.4.4)
Якщо розглядати основний (не збуджений) стан атома водню, то другою й третьою складовими в лівій частині рівняння (1.4.4) можна знехтувати. Електрон в такому стані рухається лише по коловій траєкторії і хвильова функція не залежить від q і j. Тому
 . (1.4.5)
. (1.4.5)
Хвильова функція y електрона в основному стані (1.4.5) є функцією лише r, тобто y=y( r). Такий стан називається s-станом; він має сферично-симетричний характер. Імовірність виявити електрон у заданій точці атома залежатиме лише від r. Умовам стаціонарного стану відповідає центральносиметрична функція, що легко диференціюється і має вигляд:
 , (1.4.6)
, (1.4.6)
де a ─ деяка стала величина, яка має розмірність довжини.
Необхідні похідні від (1.4.6) підставимо в (1.4.5). Після скорочення на 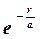 одержимо:
одержимо:
 . (1.4.7)
. (1.4.7)
Рівність (1.4.7) має місце для будь-яких значень r при виконанні таких умов:

 (1.4.8)
(1.4.8)
Розв’язавши систему рівнянь (1.4.8) відносно а і Е одержуємо:
 (1.4.9)
(1.4.9)
 (1.4.10)
(1.4.10)
Покажемо, що вираз (1.4.9) є найбільш імовірною відстанню електрона в атомі водню до ядра. Імовірність знайти електрон на відставні r від ядра, точніше в інтервалі відстаней від r до r+dr, тобто в кульковому шарі з об¢ємом dV=4pr2 dr, дорівнює:
 . (1.4.11)
. (1.4.11)
З урахуванням (1.4.6), хвильової функції основного стану маємо:
 , (1.4.12)
, (1.4.12)
де  ― густина імовірності.
― густина імовірності.
Дослідимо вираз густини імовірності на максимум, тобто похідну від w(r) прирівняємо до нуля
 ,
,
звідки
r=a. (1.4.13)
Цей результат є окремим випадком загального висновку: борівські орбіти електрона в атомі водню є геометричними місцями точок, у яких із найбільшою імовірністю можна виявити електрон.
Залежність густини імовірності w(r) виявлення електрона на різних відстанях від ядра показана на рис. 1.13.
За теорією Бора імовірність виявлення електрона у стані з n=1 відмінна від нуля лише для r=a, а згідно з висновками квантової механіки ця відстань є лише найбільш імовірною.

Рис. 1.13
Теорія Бора дає можливість визначити значення енергії електрона в будь-якому енергетичному стані, а також радіус відповідних борівських орбіт:
 , (1.4.14)
, (1.4.14)
 , (1.4.15)
, (1.4.15)
де m ― маса електрона; e ― заряд електрона; e0 ― діелектрична проникність вакууму;  ― стала Планка, поділена на 2p; n=1,2,3,...─ головні квантові числа.
― стала Планка, поділена на 2p; n=1,2,3,...─ головні квантові числа.
Зіставлення (1.4.9) і (1.4.15), а також (1.4.10) і (1.4.14) показують, що висновки квантової механіки й теорії Бора повністю збігаються. Цей збіг підкреслює значну історичну роль теорії Бора, яка ще не є квантовою, однак і не класичною теорією.
Хвильові функції для наступних основних двох енергетичних рівнів електронів у атомі водню мають вигляд
 , (1.4.16)
, (1.4.16)
 . (1.4.17)
. (1.4.17)
Ці хвильові функції також є розв¢язками рівняння (1.4.5) при умові, що  і
і  . Можна показати, що формула (1.4.14) є значенням енергії електрона на будь-якому енергетичному рівні. Однак для повного пояснення стану електрона в атомі водню необхідні ще два квантові числа, які входять у відповідні рівняння хвильових функцій і які характеризують момент імпульсу електрона в атомі.
. Можна показати, що формула (1.4.14) є значенням енергії електрона на будь-якому енергетичному рівні. Однак для повного пояснення стану електрона в атомі водню необхідні ще два квантові числа, які входять у відповідні рівняння хвильових функцій і які характеризують момент імпульсу електрона в атомі.
Для збуджених атомів хвильові функції не є центрально симетричними і залежать не лише від r, а й від q і j. Ці хвильові функції містять три цілочислові параметри, які називають квантовими числами. Серед них:
n ― головне квантове число, квантує енергію електрона – збігається з аналогічним квантовим числом теорії Бора і набуває значень від 1 до ¥;
l ― орбітальне квантове число, квантує момент імпульсу
 . (1.4.18)
. (1.4.18)
Орбітальне квантове число набуває значень l=0,1,2,... .
ml ― магнетне квантове число, квантує проекцію орбітального моменту імпульсу на вісь Z напрямку зовнішнього магнетного поля
 . (1.4.19)
. (1.4.19)
Магнетне квантове число набуває значень ml= 0,±1,±2,±3,... .
Дата добавления: 2014-12-03; просмотров: 902; Мы поможем в написании вашей работы!; Нарушение авторских прав |