Лінза. Оптична сила лінзи. Побудова зображень у лінзах

Лінзоюназивають прозоре тіло, обмежене з обох боків сферичними поверхнями (одна з поверхонь може бути плоскою).

Розрізняють такі лінзи як показано на (рис. 6.15): а - двовипукла, б - плоско-опукла, в - двоввігнута, г - плоско-ввігнута, д - опукло-ввігнута,

а) двовипу-кла	б) плоско-опукла	в) двовиг-нута	г) плоско- ввігнута	д) опукло-вігнута	е)
Рис.6.15.

Якщо товщина лінзи значна і менша від радіуса її кривизни, то таку лінзу називають тонкою. Якщо паралельний пучок променів, що падають на поверхню лінзи, лінза збирає в одній точці (фокусі), то її називають збиральною (рис. 6.16).

Якщо ж паралельний пучок променів, який падає на лінзу, лінза розсіює, то її називають розсіювальною (рис. 6.17).

Після проходження такої лінзи паралельні промені рівномірно розходяться так, що їх продовження перетинаються в уявній точці - фокусі. У збиральній лінзі фокус буде дійсним, а в розсіювальній - уявним.

Центр лінзи називають оптичним центром. Пряма лінія, яка проходить через обидва фокуси лінзи і її центр. перпендикулярно до площини лінзи, називають головною оптичною віссю, а будь-яка інша пряма, яка проходить через центр лінзи - побічною віссю. Дві площини, паралельні головній площині з обох боків лінзи, які проходять через фокуси, називають фокальними площинами. Точки перетину побічних осей з ними називають побічними фокусами. У цих точках збігаються паралельні промені (для розсіювальних лінз - їх продовження після проходження лінзи), що утворюють паралельний до даної побічної осі пучок променів.

Відстань від фокуса до оптичного центра називають фокусною відстанню лінзи (F). Фокусна відстань збиральної лінзи є додатною, а розсіювальної - від'ємною. Величину, обернену до фокусної відстані, називають оптичною силою лінзи D.

. (1)

У системі СІ оптичну силу лінзи вимірюють в діоптріях;

[D] = 1/м = 1 дптр.

Оптична сила лінзи дорівнює одній діоптрії, якщо її фокусна відстань дорівнює одному метру. Головна цінність лінзи полягає в тому, що а її допомогою можна отримати зображення предметів, які можуть світитись самі чи світяться відбитим світлом.

Якщо d - відстань від предмета до лінзи, то f - відстань від лінзи до зображення на екрані, F - фокусна відстань, то розміщення предмета і його зображення можна визначити за формулою тонкої лінзи:

. (2)

Користуючись формулою слід враховувати правило знаків:

1) якщо лінза розсіювальна, то величину F беруть зі знаком "-".

2) якщо лінза дає уявне зображення, то і f також беруть з "-".

3) якщо предмет уявний, то і d беруть зі знаком "-".

Якщо h - висота предмета, а H - висота зображення, то можна знайти збільшення лінзи:

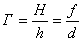. (3)

Якщо оптична система складається із декількох (D₁, D₂, …, D_n) лінз, розміщених близько одна до одної, то справедливою є така формула:

D_{системи} = D₁ + D₂ + D₃ + … + D_n (4)

Якщо ж лінзи розміщені в різних точках простору, то спочатку будують зображення першої лінзи. Це зображення служить предметом для другої лінзи і так далі. Повторюючи цей процес необхідну кількість разів, знаходять потрібне зображення для всієї оптичної системи.

У побудові зображень бере участь величезна кількість променів, хід багатьох з яких передбачити дуже важко, але в цьому і немає потреби. Для того, щоб визначити, де буде зображення, буде воно прямим чи перевернутим, збільшеним чи зменшеним, дійсним чи уявним достатньо знати хід чотирьох променів. Усі інші промені пройдуть своїм шляхом, але побудують зображення там, де отримують зображення за допомогою зручних нам променів.

Хід зручних променів:

1. Промінь, який упав на лінзу паралельно головній оптичній осі, заломившись пройде через фокус (рис.6.18, 6.19).

2. Промінь, який упав на лінзу через фокус, заломившись пройде паралельно головній оптичній осі (рис.6.20, 6.21).

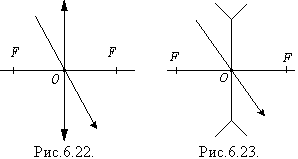
3. Промінь, який пройшов через оптичний центр, не заломлюється (рис. 6.22, 6.23).

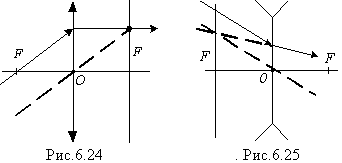
4. Промінь, який падає на лінзу паралельно побічній осі, після заломлення перетнеться з нею в фокальній площині (рис. 6.24, 6.25).

Побудова зображення у збиральній лінзі. Якщо предмет розміщений на відстані d = 2F, то його зображення буде дорівнювати за висотою предмету, буде перевернутим і дійсним, знаходитиметься в точці 2F по інший бік від лінзи (рис. 6.26).

Якщо предмет знаходиться на відстані d > 2F, зображення буде зменшеним, перевернутим, дійсним, знаходитиметься в точці між 2F i F на іншому боці від лінзи (рис. 6.27).

Якщо предмет знаходиться між 2F i F, зображення буде перевернутим, збільшеним, дійсним, знаходитиметься за 2F по інший бік від лінзи (рис. 6.28).

Якщо предмет знаходиться на відстані d = F, промені виходитимуть з лінзи паралельно до променя, що проходить через оптичний центр, і зображення не буде (рис. 6.29).

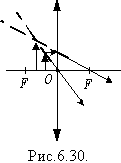
Якщо предмет знаходиться між фокусом F i оптичним центром лінзи , зображення буде прямим, уявним, збільшеним і знаходиметься по той же бік від лінзи, що і предмет (рис. 6.30).

Побудова зображення в розсіювальній лінзі. Принцип побудови завжди однаковий: така лінза робить зображення зменшеним, прямим і уявним, зображення буде знаходитися по той самий бік, що і предмет (рис. 6.31).

Побудова зображення точки, що знаходиться на головній оптичній осі в збиральній (рис.6.32) і розсіювальній (рис.6.33) лінзах.

S - точка, яка світиться, S' - її зображення.

Таке зображення можна побудувати, якщо показник заломлення лінзи є більшим від показника заломлення середовища, в якому поширюються світлові хвилі. Інакше, якщо середовище є оптично густіше від матеріалу лінзи, то збиральна лінза стане розсіювальною, і, навпаки, двовгнута - збиральною. Якщо, наприклад, у склі є опукла повітряна порожнина, то вона відіграє роль розсіювальної лінзи. Якщо повітряна порожнина двовгнута, то вона діє як збиральна лінза.

Пояснюється це тим, що, наприклад, двоопуклу лінзу можна схематично уявити як сукупність призм (рис. 6.34). Якщо середовище, що оточує лінзу, є оптично густішим від матеріалу лінзи, то лінза буде розсіювальною, оскільки світлові промені відхиляються від основ призм (рис. 6.35).

Лінза є головною частиною багатьох оптичних приладів (фотоапаратів, проекційних апаратів, телескопів, біноклів, підзорних труб, лупи, мікроскопа), ока людини або тварин. Побудова фотоапаратів подібна до зображеної на рис. 6.27, у проекційних апаратів - на рис. 6.28, а у мікроскопі та лупі - на рис. 6.30.

Запитання для самоперевірки

1. Що називають лінзою ? Яку лінзу називають випуклою, а яку ввігнутою ? Які види лінз існують ?

2. Яку лінзу називають тонкою ? Що таке оптичний центр тонкої лінзи ? Що називають головною оптичною віссю лінзи ? Побічною оптичною віссю лінзи ?

3. Що називають фокусом лінзи ? У якому випадку фокус лінзи дійсний, а в якому уявний ? Що називають фокусною відстанню ?

4. Поясніть усі випадки побудови зображень у збиральній лінзі.

5. Поясніть усі випадки побудови зображень для розсіювальної лінзи.

6. Наведіть формулу тонкої збиральної лінзи. Який вигляд має ця формула для розсіювальної лінзи?

7. Що називають уявним збільшенням лінзи ? За якою формулою визначаютьлінійне збільшення лінзи ?

8. Що називають оптичною силою лінзи ? У якому разі оптична сила лінзи є додатною, а в якому від'ємною ? У яких одиницях виміряють оптичну силу лінзи?

9. Що називають акомодацією ока ? Що таке найближча точка акомодації ? Далека точка акомодації ? Де знаходяться ці точки ?

10. Що називають кутом зору? Яким має бути кут зору між розглянутими деталями предмета, щоб око бачило ці деталі роздільно?

11. Що називають відстанню найкращого зору? Чому дорівнює ця відстань для нормального ока ?

12. Який дефект зору називають далекозорістю? Короткозорістю? Яким шляхом виправляють ці дефекти? Відповіді поясніть за допомогою рисунків.

13. Що називають лупою? Для чого її призначено? Зобразіть хід променів у лупі. За якою формулою визначають лінійне збільшення лупи ?