
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Порівняння відрізків, дії над відрізками. Натуральне число як результат вимірювання величини. Натуральне число як міра величини. Натуральне число як міра відрізка.
2. Ми розглянули кількісну (теоретико-множинну) і аксіоматичну (порядкову) теорії цілих невід’ємних чисел. У практичній діяльності людини ці числа використовуються для лічби. Кількісна теорія дає можливість з’ясувати, скільки є елементів в деякій скінченій множині, а порядкова теорія дозволяє встановити в множині певний порядок і з’ясувати, яким по порядку розміщується той чи інший елемент. Виявляється, що у практичній діяльності людини доводиться, чи не частіше, виконувати операцію вимірювання величин (довжина, маса, площа, об’єм тощо). Для цього теж доводиться користуватися цілими невід’ємними числами. З цією метою в математиці відповідно до практичних потреб людини довелося побудувати ще одну теорію цілих невід’ємних чисел. У цій теорії ціле невід’ємне число розглядається як результат вимірювання величини. Розкриємо сутність цієї теорії на прикладі натурального числа як результату вимірювання довжини відрізків.
Якщо є два відрізка a і b, то порівняти їх можна двома способами: 1) безпосередньо, накладанням; 2) опосередковано, за допомогою третього відрізка. У другому випадку досить часто використовують так званий одиничний відрізок (позначають е). Сутність процесу вимірювання за допомогою одиничного відрізка полягає в тому, що ми послідовно відкладаємо його на заданому відрізку. При цьому можливі два випадки:
1) після деякого відкладання кінець одиничного відрізка співпав з кінцем заданого відрізка. В цьому випадку процес вимірювання закінчується і довжина відрізка виражається натуральним числом, яке показує, скільки разів одиничний відрізок вміщається в даному відрізку. Це число і називають мірою заданого відрізка при заданому одиничному відрізку е.Символічно це позначають так: me(a). Цей запис читають так: міра відрізка а при одиничному відрізку е або m від a при одиничному відрізку е. Так символічний запис me(a)=k означає, що одиничний відрізок е вмістився у даному відрізку k разів;
2) після деякого відкладання одиничного відрізка на заданому відрізку залишиться відрізок, менший, ніж одиничний. У цьому випадку результат вимірювання в загальному випадку не буде виражатися натуральним числом і процес вимірювання не буде закінчуватися. Результатом порівняння довжин двох відрізків може бути один із трьох випадків: 1) а=b; 2) а>b; 3) а<b. Вказані випадки можна проілюструвати на наступних малюнках №№ 3.2-3.4.
а
 А
А

О в В
Малюнок № 3.2. Відрізки ОА=а і ОВ=b рівні.
 а А
а А

О в В
Малюнок № 3.3. Відрізок ОА=а більший за відрізок ОВ=b (а>b).
 а А
а А

О в В
Малюнок № 3.4. Відрізок ОА=а менший за відрізок ОВ=b (а<b).
Таким чином, на множині відрізків ми задали відношення рівності відрізків, яке має властивості рефлексивності, симетричності та транзитивності, тобто є відношенням типу еквівалентності, та відношення “менше” (“більше”), яке є відношенням строгого порядку. Як відомо із шкільного курсу математики, над відрізками можна виконувати операції: а) додавання та віднімання відрізків; б) множення та ділення відрізка на натуральне число. Визначимо ці операції над відрізками.
Означення: відрізок а є сумою відрізків а1, а2, а3, ..., аn, якщо вони лежать на одному й тому ж самому промені, не мають жодної спільної внутрішньої точки та кінець кожного попереднього відрізка є початком наступного.
Операція додавання відрізків підкоряється комутативному (переставному) та асоціативному (сполучному) законам. Щоб побудувати відрізок, який є сумою відрізків а1, а2, а3, ..., аn потрібно на довільній прямій від довільної точки послідовно відкласти один за одним задані відрізки, а тоді відрізок, який знаходиться між обраною точкою та кінцем останнього із відкладених відрізків, і буде сумою відрізків а1, а2, а3, ..., аn. Проілюструємо це за допомогою наступного малюнка № 3.5.
Операцію віднімання відрізків визначимо з допомогою наступного означення.
Означення: різницею двох заданих відрізків а та b називають такий третій відрізок с=а-b, який в сумі з відрізком b дає нам відрізок а, тобто (а-b)+b=а.
Щоб побудувати різницю двох відрізків, потрібно на довільній прямій від довільної точки відкласти відрізок а і від одного із його кінців відкласти відрізок b. Тоді різницею а-b двох відрізків а і b буде відрізок, що залишиться. Проілюструємо це з допомогою наступного малюнка № 3.6.
а1 а2 а3 …. аn

а1+а2+а3+...+аn
Малюнок № 3.5. Сума відрізків а1, а2, а3, ..., аn.

а

b а-b
Малюнок № 3.6. Різниця а-b відрізків.
Операції множення та ділення відрізка на натуральне число визначимо з допомогою наступних означень.
Означення: добутком даного відрізка а на натуральне число n називається сума n-відрізків, кожен із яких дорівнює а.
Означення: діленням даного відрізка а на натуральне число n називається відшукання 1/n частини відрізка а.
Щоб побудувати відрізок, який дорівнює добутку даного відрізка на натуральне число n потрібно на довільній прямій від вибраної точки послідовно відкласти заданий відрізок n разів. Щоб поділити заданий відрізок на n рівних частин, тобто знайти 1/n цього відрізка, слід через один із кінців відрізка а провести промінь під довільним кутом. На промені відкласти довільним розхилом циркуля n однакових відрізків і сполучити кінець n-го відрізка з іншим кінцем даного відрізка і через точки поділу провести паралельні прямі. Графічну сутність цих операцій проілюструємо на наступних малюнках №№ 3.7-3.8.
 а а а а
а а а а

а×n
Малюнок № 3.7. Добуток відрізка а на натуральне число n.
 а:n
а:n
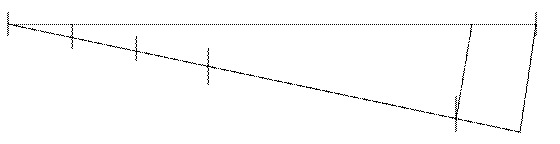
Малюнок № 3.8. Ділення даного відрізка а на натуральне число n (  відрізка а).
відрізка а).
Задача вимірювання довжини даного відрізка а зводиться до вибору деякого одиничного відрізка е з наступним порівнянням даного відрізка а з одиничним відрізком е. Вимірюючи довжину даного відрізка за допомогою даного одиничного відрізка е, ми відкладаємо одиничний відрізок е на заданому відрізку а, підраховуємо, скільки разів відрізок е вмістився в заданому відрізку а. Якщо одиниця вимірювання е вкладається ціле число разів у заданому відрізку а, то процес вимірювання закінчено і результат вимірювання записують так: а=е+е+е+...+е=n·е або me(a)=n. В цьому випадку говорять, що натуральне число n є числовим значенням відрізка а при одиниці довжини е. Отже, можна прийняти таке означення.
Означення: якщо відрізок а можна розбити на n відрізків, кожен з яких дорівнює одиничному відрізку е, то число n називають мірою відрізка а чи значенням довжини відрізка а і пишуть n=mе(а).
Виберемо одиничний відрізок е та розглянемо множину всіх таких відрізків, у яких одиничний відрізок вміщується ціле число разів. Розіб’ємо цю множину відрізків на класи, спільною властивістю яких буде: мати однакову міру. Тоді кожне натуральне число буде мірою якогось класу відрізків. Враховуючи сказане, приймемо наступне означення.
Означення: Натуральним числом як результатом вимірювання величини називається числове значення міри величини а при вибраній одиничній мірі е.
Означення: натуральне число n як міра відрізка а показує, із скількох одиничних відрізків е складається відрізок а.
Можна строго математично довести, що для кожного натурального числа існує відрізок, для якого це число є його мірою. Обернене твердження буде хибним. Можна довести, що при вибраній одиниці вимірювання е для будь-якого відрізка а його міра, тобто натуральне число n=mе(а), яке є його мірою, існує і єдине. Зазначимо, якщо за одиничний вибрати інший відрізок, то числове значення довжини відрізка зміниться, наприклад: якщо для даного відрізка довжиною 10 см одиничним вибрати 1 мм, то його мірою буде натуральне число 100; якщо 1 см, то – число 10; якщо 1 дм, то - число 1.
Розглянемо, який же зміст мають відношення “дорівнює”, “менше”, “більше” для натуральних чисел, які є результатом вимірювання довжини відрізка. Нехай нам задано два відрізка а і b. Виберемо одиничний відрізок е і нехай а=n×е (або me(a)=n) і b=k×e (me(b)=k). Для натуральних чисел, які розглядаються як міра довжини, можна задати відношення рівності та “менше” (“більше”). Якщо відрізки а і b рівні, то рівні і їх числові значення довжини, тобто [а=b]Þ[mе(а)=mе(b)Ûn=k]. Якщо відрізок а більший за відрізок b, то і його числове значення довжини mе(а) більше за числове значення mе(b), тобто [а>b]Þ[me(a)>me(b)Ûn>k]. Аналогічно, якщо [а<b]Þ[ me(a)<me(b)Ûn<k]. Легко переконатися, що відношення “дорівнює” на множині відрізків має властивості рефлективності, симетричності і транзитивності, тобто є відношенням типу еквівалентності, а відношення “менше” є відношенням строгого порядку. Такий взаємозв’язок між відрізками і числовими значеннями їхніх довжин дозволяє зводити порівняння відрізків до порівняння їхніх відповідних числових значень довжини, тобто до порівняння натуральних чисел, і навпаки. Натуральне число можна розглядати теж як результат вимірювання маси, площі, об’єму, вартості, часу тощо.
Дата добавления: 2014-12-03; просмотров: 444; Мы поможем в написании вашей работы!; Нарушение авторских прав |