
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кратковременные нагрузки.
· Гололедные нагрузки. Если возможно обледенение трубопровода, то нормативное значение гололедного давления на поверхность определяется по формуле 14 СНиП 2.01.07-85 «Нагрузки и воздействия»
 (8.20) где
(8.20) где  – толщина стенки гололеда, превышаемая раз в пять лет;
– толщина стенки гололеда, превышаемая раз в пять лет;
 – коэффициент, учитывающий изменение толщины стенки гололеда по высоте, для трубопроводов принимается равным единице
– коэффициент, учитывающий изменение толщины стенки гололеда по высоте, для трубопроводов принимается равным единице  = 1,0;
= 1,0;
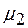 – коэффициент, учитывающий отношение площади элемента, подверженного обледенению, к полной площади элемента, для трубопровода
– коэффициент, учитывающий отношение площади элемента, подверженного обледенению, к полной площади элемента, для трубопровода 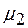 = 0,6;
= 0,6;
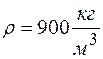 - плотность льда;
- плотность льда;
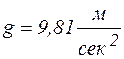 .
.
Нормативные нагрузки от обледенения на один метр трубы вычисляются по формуле
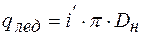 , (8.21)
, (8.21)
которая после подстановок может быть представлена так, как в СНиП 2.05.06-85
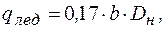 (8.22)
(8.22)
где  – толщина льда в
– толщина льда в 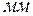 ;
;
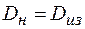 – диаметр наружный трубы или изоляции в
– диаметр наружный трубы или изоляции в 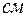 .
.
Коэффициент надежности по нагрузке для гололеда 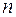 =1,3.
=1,3.
· Нормативная снеговая нагрузка на горизонтальную проекцию надземного трубопровода
 (8.23)
(8.23)
где  – коэффициент перехода от веса снегового покрытия горизонтальной поверхности земли к снеговой нагрузке на трубопровод (
– коэффициент перехода от веса снегового покрытия горизонтальной поверхности земли к снеговой нагрузке на трубопровод (  =0,4);
=0,4);
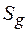 – нормативное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли, которое выбирается по таблице 4 для соответствующего снегового района Российской Федерации;
– нормативное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли, которое выбирается по таблице 4 для соответствующего снегового района Российской Федерации;
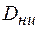 – диаметр изоляции или наружный диаметр трубы.
– диаметр изоляции или наружный диаметр трубы.
Таблица 4. Нормативные значение веса снегового покрова (таблица 4 СНиП 2.01.07-85)
| Снеговые районы Российской Федерации | I | II | III | IV | V | VI | VII | VIII |
| Sg, кПа | 0,8 | 1,2 | 1,8 | 2,4 | 3,2 | 4,0 | 4,8 | 5,6 |
· Ветровая нагрузка действует перпендикулярно осевой вертикальной плоскости одиночно проложенного трубопровода
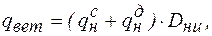 (8.24)
(8.24)
где 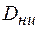 – наружный диаметр с учетом изоляции;
– наружный диаметр с учетом изоляции;
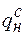 ,
,  – нормативное значение статической и динамической составляющих ветровой нагрузки, Н/м2 (СНиП 2.01.07-85 “ Нагрузки и воздействия”).
– нормативное значение статической и динамической составляющих ветровой нагрузки, Н/м2 (СНиП 2.01.07-85 “ Нагрузки и воздействия”).
Статическую составляющую ветровой нагрузки определяют по величине скоростного напора
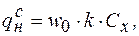 (8.25)
(8.25)
где 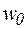 – нормативное значение ветрового давления;
– нормативное значение ветрового давления;
 - коэффициент, учитывающий изменение ветрового давления по высоте;
- коэффициент, учитывающий изменение ветрового давления по высоте;
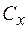 – аэродинамический коэффициент лобового сопротивления надземного трубопровода.
– аэродинамический коэффициент лобового сопротивления надземного трубопровода.
Величина скоростного напора определяется в зависимости от района расположения трубопровода (таблица 5).
Таблица 5. Нормативные значения ветровой нагрузки (таблица 5 СНиП 2.01.07-85)
| Ветровые районы СССР | Ia | I | II | III | IV | V | VI | VII |
| w0, кПа | 0,17 | 0,23 | 0,30 | 0,38 | 0,48 | 0,60 | 0,73 | 0,85 |
В некоторых случаях нормативное значение ветрового давления 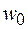 допускается устанавливать на основе данных метеостанций Госкомгидромета, а также результатов обследования районов строительства с учетом опыта эксплуатации сооружений. При этом нормативное значение ветрового давления
допускается устанавливать на основе данных метеостанций Госкомгидромета, а также результатов обследования районов строительства с учетом опыта эксплуатации сооружений. При этом нормативное значение ветрового давления 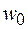 , Па, следует определять по формуле
, Па, следует определять по формуле
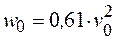 (8.26)
(8.26)
где  - численно равно скорости ветра, м/с, на уровне 10 м над поверхностью земли наибольший за пять лет.
- численно равно скорости ветра, м/с, на уровне 10 м над поверхностью земли наибольший за пять лет.
Аэродинамический коэффициент 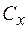 определяется в зависимости от числа Рейнольдса (критерий подобия в гидроаэродинамике) по диаграмме на рисунке 23.
определяется в зависимости от числа Рейнольдса (критерий подобия в гидроаэродинамике) по диаграмме на рисунке 23.
Число Рейнольдса определяется по законам гидроаэродинамики
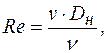 (8.27)
(8.27)
где 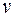 – скорость ветра, м/с;
– скорость ветра, м/с;
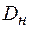 – характерный линейный размер, м;
– характерный линейный размер, м;
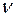 – кинематическая вязкость воздуха (при t=15oC и Pатм=1000 гПа принимают
– кинематическая вязкость воздуха (при t=15oC и Pатм=1000 гПа принимают 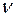 =0,146.10-4 м2/с).
=0,146.10-4 м2/с).
Если число Рейнольдса Re>35.105, принимают аэродинамический коэффициент 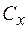 =0,7.
=0,7.
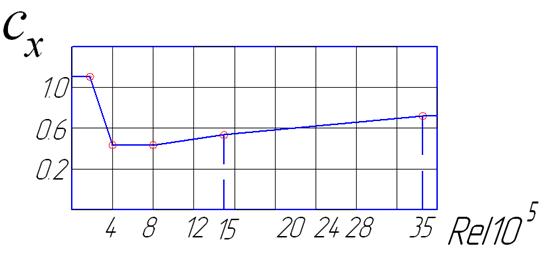
Рисунок 23. Диаграмма для определения аэродинамического коэффициента.
Динамическую составляющую ветровой нагрузки определяют по формуле
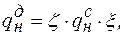 (8.28)
(8.28)
где  – коэффициент пульсации скоростного напора (СНиП 2.01.07-85);
– коэффициент пульсации скоростного напора (СНиП 2.01.07-85);
ξ – коэффициент динамичности, зависящий от периода колебаний участка трубопровода 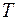 , соответствующего второй форме свободных горизонтальных колебаний и от логарифмического декремента колебаний надземного трубопровода ∂ (рисунок 24).
, соответствующего второй форме свободных горизонтальных колебаний и от логарифмического декремента колебаний надземного трубопровода ∂ (рисунок 24).

Рисунок 24. Диаграмма для определения коэффициента динамичности.
Если период колебаний 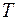 <0,25с, то динамическая составляющая не учитывается, т.е.
<0,25с, то динамическая составляющая не учитывается, т.е.  =0.
=0.
Логарифмический декремент колебаний  трубопровода зависит от конструктивной схемы надземного перехода и может определяться по записям виброграмм свободных затухающих колебаний (рисунок 25).
трубопровода зависит от конструктивной схемы надземного перехода и может определяться по записям виброграмм свободных затухающих колебаний (рисунок 25).
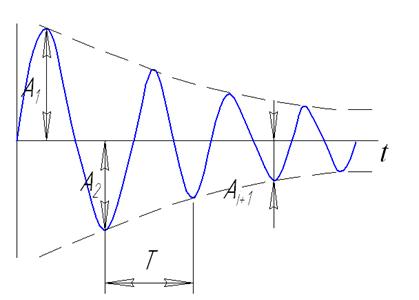
Рисунок 25. Диаграмма свободных затухающих колебаний.
Амплитуды последовательных периодов затухающих колебаний образуют геометрическую прогрессию
 (8.29)
(8.29)
где 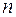 – неизвестная постоянная определяемая опытным путем так же, как период колебаний
– неизвестная постоянная определяемая опытным путем так же, как период колебаний 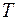 .
.
Тогда логарифмический декремент колебаний будет определяться
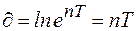 . (8.30)
. (8.30)
Для предварительных расчетов (пока не известны все необходимые размеры) логарифмический декремент колебаний  принимается для горизонтальных колебаний
принимается для горизонтальных колебаний  =0,05, а для вертикальных колебаний
=0,05, а для вертикальных колебаний  =0,03-0,05.
=0,03-0,05.
Для определения периода собственных колебаний 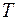 находят частоту собственных изгибных колебаний
находят частоту собственных изгибных колебаний 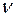 . Тогда
. Тогда 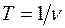 .
.
Коэффициент надежности для ветровой нагрузки 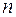 =1,2.
=1,2.
· Нагрузка, вызываемая морозным растрескиванием грунта. Коэффициент надежности по нагрузке 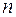 = 1,2.
= 1,2.
· Нагрузки и воздействия, возникающие при пропуске очистных устройств. Коэффициент надежности по нагрузке 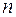 = 1,2.
= 1,2.
· Нагрузки и воздействия, возникающие при испытании трубопроводов. Коэффициент надежности по нагрузке 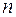 = 1,0.
= 1,0.
· Воздействие селевых потоков и оползней. Коэффициент надежности по нагрузке 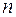 = 1,0.
= 1,0.
Дата добавления: 2014-12-23; просмотров: 310; Мы поможем в написании вашей работы!; Нарушение авторских прав |