Виды средних величин.

Выбор вида средней величины зависит от характера, содержания изучаемого явления и имеющихся исходных данных.

Виды средних величин:

1. Степенные средние: средняя арифметическая; средняя гармоническая; средняя геометрическая; средняя квадратическая и др.

Степенные средние величины могут выступать в двух формах: простой и взвешенной. Простая средняя применяется при вычислении средней по первичным (несгруппированным) данным, взвешенная средняя – по сгруппированным данным.

Формула степенной средней для несгруппированных данных в общем виде записывается следующим образом:

Вид степенной средней зависит от показателя степени k. Виды степенных средних величин и их формулы представлены в таблице:

Вид средней величины	Значение степени k	Формула средней
простая	взвешенная
1. Средняя гармоническая	–1
2. Средняя геометрическая
3. Средняя арифметическая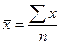
4. Средняя квадратическая

Условные обозначения:

– средняя величина;

– варианта осредняемого признака;

– число признаков;

– вес варианты (частота повторения признака).

При использовании одних и тех же исходных данных, чем больше значение степени k в формуле степенной средней, тем больше значение средней величины:

,

т. е. средние величины ранжируются по показателю степени k.

Соотношение степенных средних, выраженное в виде данного неравенства, называется в статистике свойством мажорантности средних.

2. Средняя хронологическая – вид средних величин, используемый при осреднении уровней моментных рядов динамики:

3. Структурные средние: мода, медиана (см. тему 7).

Самым распространенным видом средних величин является средняя арифметическая.

Другие виды средних используются реже, для специальных целей. Так, средняя геометрическая применяется для расчета среднего темпа роста в рядах динамики (см. тему 8). Средняя гармоническая – это величина, обратная средней арифметической из величин, обратных данным. Средняя квадратическая используется для определения показателей вариации (см. тему 7). Средняя хронологическая необходима для исчисления среднего уровня в моментных рядах динамики
(см. тему 8). Структурные средние (мода и медиана) применяются для характеристики вариационных рядов распределения (см. тему 7).