Основные свойства средней арифметической величины.

Средняя арифметическая является наиболее часто используемым видом средних величин. Основные свойства средней арифметической:

1. Сумма отклонений вариант от средней арифметической величины равна нулю.

2. Сумма квадратов отклонений вариант от средней арифметической меньше суммы квадратов отклонений вариант от произвольно выбранного числа А.

3. Средняя арифметическая из постоянных величин равна этой постоянной величине.

4. Если каждую варианту х увеличить или уменьшить на величину А, то средняя увеличится или уменьшится на ту же величину А.

5. Если каждую варианту х увеличить или уменьшить в К раз, то и средняя увеличится или уменьшится в К раз.

6. Если при расчете средней арифметической взвешенной увеличить или уменьшить все веса в С раз, то средняя не изменится.

На использовании свойств средней арифметической основан
метод моментов – способ, применяемый для упрощения расчета средней арифметической величины. Для этого необходимо:

1) уменьшить все варианты х на одно и то же число А, взяв за отсчет некоторый произвольный условный нуль;

2) полученные величины уменьшить в некоторое число раз (К);

3) из преобразованных величин вычислить условную среднюю арифметическую ;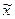

4) умножить эту условную среднюю 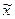на К и, прибавив результат к А, получить действительное значение искомой средней .

В целом, при вычислении средней арифметической с использованием метода моментов расчетная формула будет иметь следующий вид: