Формула степенной средней взвещенной в общем виде

где:

§ — частота повторения -й варианты.

В зависимости от того, какое значение принимает показатель степени средней величины , получаем различные виды средних:

При расчете различных степенных средних по одним и тем же данным значения средних будут неодинаковыми. Чем выше показатель степени ( ), тем больше величина средней, т.е. действует правило мажорантности средних:

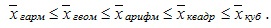
12. 1) Самый распространенный вид средней величины - это средняя арифметическая.

В общем случае ее расчет сводится к суммированию всех значений варьирующего признака и делению полученной суммы на количество единиц совокупности.

Средняя арифметическая может быть:

а) средняя арифметическая простая

x_i - варианты осередняемого признака

n- число единиц совокупности

Средняя арифметическая простая применяется в тех случаях, когда значение каждого варианта встречается по одному разу

б) В тех случаях, когда значение вариантов встречаются несколько раз, для расчет применяют среднюю арифметическую взвешанную.

f_i - частота этих вариантов.

В случае определения средней величины в интервальном ряду распределения сначала переходят от интервального к дискретному ряду, т.е. находят середину интервалов в каждой группе, как полусумму нижней и верхней границ в каждой группе.

2) Средняя гармоническаяприменяется в тех случаях, когда известны варианты осередняемого признака (x_i) и показатели, представляющие произведение вариантов на частоты или веса средней арифметич.

Это произведение x*f=F и служит в качестве весов или частот средней гармонической.

Средняя гармоническая может быть простой и взвешанной.

а) средняя гармоническая простая

x_i - варианты осередняемого признака

n- число вариантов осередняемого признака

Средняя гармоническая простая применятся в тех случаях, когда веса всех вариантов равны. В тех случаях, когда веса не равны, применяется средняя гармоническая взвешанная.

б) средняя гармоническая взвешанная

Средняя гармоническая - это средняя из обратных величин, поэтому ее применяют для расчета средней трудоемксти, которая является обратной величиной производительности труда (выработки).

На практике чаще всего применяются средняя арифметическая и средняя гармоническая. Чтобы правильно выбрать формулу средней, необходимо руководствоваться следующими правилами:

1. Средняя гармоническая применяется для расчета в тех случаях, когда показатеь, величина которого не известна находится в знаменателе исходного отношения (это экономическое содержание расчитываемое показателем)

ЗП=ФондЗП/ЧР

2. Если в искомом отношении не известен числитель, то для расчета применяют среднюю арифметическую взвешенную.

3) Средняя геометрическаяприменяется в тех случаях, когда определяемый показатель является не суммой значения признака, а их произведением, т.е. во всех случаях, где варианты связаны между собой не знаком «+», а знаком «*» расчитывают не среднюю арифметическую, а среднюю геометрическую. Средняя гармоническая бывает простая и взвешанная.

а) средняя геометрическая простая

x_i - варианты осередняемого признака; n- число вариантов осередняемого признака

Применяется, когда варианты встречаются по одному разу.

В тех случаях, когда разное число вариантов, применяется

б) средняя геометрическая взвешенная

Ср. геом. простая применяется в экономических исследованиях для расчета среднего коэффициента роста. Ср. геом. взвешенная применяется для расчета средних величин, когда значения признака заключены в групповые интервалы. В этих случаях в качестве значения признака необходимо брать не значение их середины интервала, а log их полусуммы.

4) Средняя квадратичная применяется при осереднении величин, выраженных в виде квадратичной функции.

Простая.

Применяется, когда варианты встречаются по одному разу. Применяется на практике редко. Ее используют в основном для расчета средних диаметров труб, средних сторон квадрата.

Между перечисленными средними величинами, рассчитанными по одной и той же совокупности единиц и по одному и тому же признаку существует следующая взаимосвязь:

5) Средняя хронологическая применяется для расчета средних величин в моментных рядах, когда значения признака представлены в хронологическом порядке через равные промежутки времени.

1.01.09.

1.02.09.

1.03.09.