Импульс как фундаментальная характеристика объекта

Как следует из опыта, масса является инвариантной величиной, одинаковой во всех инерциальных системах отсчета. Она в равной мере характеризует и покоящийся, и движущийся материальные объекты, моделируемые частицей. По этой причине она не содержит информации о движении объекта в так называемой лабораторной системе отсчета, которую мы условно принимаем за неподвижную. Скорость объекта, как говорилось выше, хотя она и связана с движением, также нельзя считать полноценной фундаментальной характеристикой движущегося объекта.

Ньютон первым предложил в качестве фундаментальной характеристики движения использовать их комбинацию. При малых скоростях она называется нерелятивистским импульсом р и для частицы имеет вид произведения массы на скорость р=mu. Это векторная величина, как оказалось, имеет универсальный смысл, а именно: импульс можно сопоставить объекту не только в модели частицы, но и в других, основанных на ней моделях. Она ориентирована в направлении скорости движения и обладает необходимым свойством сохранения для свободных объектов.

Другую комбинацию из тех же исходных характеристик (массы и скорости) предложил Лейбниц. Ее историческое название «живая сила» со временем было вытеснено современным термином – кинетическая энергия. Это скалярная величина, обозначаемая символом е_кин, вычисляется для нерелятивистских движений по известной формуле 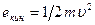. Естественно, что данная величина для свободных объектов также остается постоянной в силу постоянства скорости.

В течение почти ста пятидесяти лет шел спор о том, какая из этих двух величин является предпочтительной, тем более что они взаимосвязаны следующим отношением: 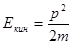. Сначала победа оставалась за импульсом, но за тем выяснилось, что и кинетическая энергия имеет свои преимущества. В настоящее время как физические величины обе они приобрели равноправие. Но при этом выяснились два обстоятельства. Первое заключается в том, что приведенная выше формула для кинетической энергии является приближенной, справедливой лишь для медленных движений, а потому требующей уточнения. Второе обстоятельство состоит в том, что кинетическая энергия – это лишь часть другой, более общей фундаментальной характеристики – полной энергии.

Приведенное выше выражение для импульса также справедливо только при малых скоростях. В общем случае вводится релятивистский импульс 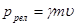, где 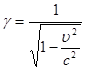(6.1).

Нетрудно видеть, что при релятивистских движениях, когда, несмотря на воздействие окружения, скорость частицы становится практически постоянной, импульс р_рел продолжает расти. Иными словами, в этом пределе импульс практически уже не зависит от ее скорости (именно это свойство характерно для импульса света). Сказанное позволяет предположить, что, несмотря на то, что определение импульса основано на скорости, тем не менее, он является самостоятельной физической величиной.

Универсальность импульса как физической характеристики можно продемонстрировать на модели системы частиц. Чтобы проделать это, рассмотрим целый ряд внешне совершенно различных процессов, таких как упругое столкновение биллиардных шаров, распад или слияние ядер или молекул, вылет ракеты за пределы солнечной системы или падение на некую планету кометы из галактического пространства. Все эти процессы сближает то обстоятельство, что к ним можно применить модель изолированной системы материальных объектов. Особенность такой системы состоит в том, что всё ее движение как целого, если смотреть на нее издалека, вовсе можно моделировать одной свободной частицей.

За счет внутренних свойств, которые сейчас мы рассматривать не будем, система может трансформироваться различным образом, наконец, исходные свободные частицы могут сталкиваться между собой и затем либо просто разлетаться в разные стороны, качественно не меняясь, либо рождать вместо себя другие свободные частицы, которые затем также разлетаются. Совокупность таких процессов принято обобщенно называть столкновениями.

Как показала практика, таким системам в любой ИСО также можно сопоставить векторную величину, называемую импульсом системы 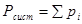, где р_i – импульс каждой отдельной частицы в данной ИСО. Эта величина, по определению, является аддитивной как для релятивистских, так и нерелятивистских движений. При этом она обладает свойством сохранения во всех процессах, описанных выше. Импульс с полным основанием можно считать фундаментальной физической характеристикой движения.

Пользуясь импульсом, можно определить и скорость системы частиц V, если ее как целое можно моделировать одной частицей

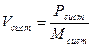(6.2).

Для изолированных систем она также сохраняется, что является обобщением закона инерции на такие системы.На примере импульса можно показать, насколько неслучайным оказывается выбор истинно фундаментальных характеристик движения. Ведь они раскрывают нюансы пространственно-временного поведения объекта и потому должны нести в себе «отпечатки» свойств пространства-времени. В настоящее время установлена взаимосвязь между ними. Так, оказалось, что свойство импульса сохраняться для изолированных объектов напрямую связано с однородностью пространства, которая проявляется в равноправии всех ИСО, отличающихся друг от друга сдвигом начала системы отсчета вдоль каждой из декартовых осей координат. Если бы пространство не обладало однородностью, импульс не обладал бы качествами фундаментальной характеристикой.