Полная энергия и полный момент как фундаментальные характеристики объекта

Энергию в самом общем случае можно сопоставить со способностью системы производить работу. Обратимся вновь к кинетической энергии. Она определяет возможность тела совершить работу за счет своего движения (скорости). Так, например, пуля только налету может пробить стену. Поэтому, на первый взгляд, свободное покоящееся тело никакой энергией не обладает (мы пока не имеем в виду случай, когда тело находится в покое, будучи при этом подверженным действию внешнего поля – электрического, гравитационного). Иными словами, мы неявно предполагаем, что у свободного тела может быть только кинетическая энергия е_кин.

Однако, как установил А. Эйнштейн, в общем случае это уже не так и энергия свободной частицы е имеет более глубокий смысл – полной энергии частицы. Он показал, что она по-прежнему зависит от квадрата скорости, но не непосредственно, а через функциюg (u²), уже встречавшуюся нами ранее, так что:

(6.3).

Это выражение знаменательно тем, что оно справедливо и при релятивистских скоростях движения частицы.

Используя некоторые математические преобразования, полную энергию можно тождественно представить в виде , где слагаемое е₀ не обращается в нуль даже в состоянии покоя ( ) и потому носит название энергии покоя. Таким образом, даже покоящееся в некоторой ИСО тело при определенных условиях способно производить работу. Второе слагаемое е_кин, будучи отличным от нуля только для движущейся частицы, как и прежде, называется кинетической энергией, однако теперь она вычисляется по иной формуле:

(6.4).

Справедливость этого выражения подтверждается тем, что при малых скоростях оно переходит в привычную формулу . Однако проведенное обобщение показывает, что физически значимой величиной и в этих условиях оказывается полная энергия е, вычисляемая как .

Полная энергия для совокупности свободных частиц аддитивна:

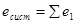(6.5).

Более глубокое обобщение связано с рассмотрением релятивистского импульса и полной энергии свободной частицы с позиций концепции единого пространства-времени. Она подразумевает инвариантность этих величин при произвольных скоростях по отношению к любой ИСО. Каждая из этих двух величин – импульс и полная энергия – при смене системы отсчета, конечно, изменяется. Но обе эти величины, как показал Эйнштейн, в едином пространстве – времени не существуют раздельно. Они рассматриваются совместно как компоненты единой обобщенной физической величины, называемой в мире событий четырехмерным вектором «энергии – импульса». Различные компоненты этой величины – полная энергия и импульс – при смене ИСО преобразуются друг через друга. Но при этом квадрат длины этого четырехмерного вектора в мире событий остается неизменным во всех ИСО – он определяется двумя инвариантами – массой частицы и скоростью света в пустоте.

В общем случае можно получить еще две полезные формулы:

и (6.6).

Казалось бы, можно ограничиться только рассмотрением полной энергии. Однако даже в рамках классического подхода эти величины дают разную информацию о движении: импульс – это вектор, связанный с направлением скорости, а полная энергия – скаляр, включающий и энергию покоя. Уже поэтому только их совокупность позволяет представить движение частицы полностью.

Кроме того, как видно из выражения для полной энергии, возможны ситуации, когда-либо импульс вместе с кинетической энергией, либо энергия покоя по отдельности равны нулю. Первый случай соответствует состоянию покоя обычной частицы. Второй – связан с особыми «частицами». К этой категории принадлежат частицы света и нейтрино (легчайшие из элементарных частиц). Учитывая, что они имеют скорость c, в пустоте строго равную с, для величин их импульса получим выражение , так что их энергия покоя и масса оказывается равными нулю. Теперь видно, что полная энергия для света и нейтрино всегда (а для других частиц – при околосветовых скоростях) имеет смысл кинетической энергии.

Кроме того, она обладает необходимым свойством сохранения как для модели одной свободной частицы, так и для модели системы частиц, не испытывающих внешних воздействий. Однако заметим, что энергия покоя и кинетическая энергия по отдельности этими качествами не обладают. Это открывает широкие возможности для взаимных превращений различных форм энергии.

Однородность как важнейшее свойство пространства и времени нашла отражение в двух фундаментальных характеристиках материи – импульсе и полной энергии. Возникает вопрос, существует ли особая фундаментальная характеристика, связанная с еще одним важным свойством пространства – изотропностью, которое заключается в равноправии всех направлений в пространстве. Положительный ответ на него сопровождается некоторыми оговорками. Дело в том, что искомая величина не может быть введена для классической модели частицы, чтобы ощутить изотропность, необходимо совершить вращение, которое частица выполнить принципиально не может, поскольку она имеет размер геометрической точки.

С классической точки зрения, всякое вращение подразумевает наличие протяженной материальной системы. Ею может быть либо электромагнитное излучение в модели континуума, либо вещество в модели системы частиц. Такие объекты, как правило, вращаются как целое вокруг некой оси, причем каждая из частиц (или каждый малый элемент континуума) движется по окружности в одной из плоскостей, перпендикулярных оси вращения. Поэтому искомая характеристика в рамках классической стратегии познания может быть введена для моделей распределенных материальных систем, в которых возможно вращение.

Геометрической характеристикой темпа вращения служит угловая скорость w. Пытаясь раскрутить коробок спичек, нетрудно убедиться в том, что эффективность вращения будет зависеть от того, как он ориентирован относительно оси вращения. Отсюда можно заключить, что угловая скорость вращения регулируется распределением массы внутри системы, поэтому ее инертные свойства в данном случае не могут характеризоваться одной только системы. Для этого требуется особая характеристика, в которой учитывалась бы «объемность» объекта и его симметричность по отношению к оси вращения (конфигурация массы). Именно поэтому она должна выражаться через некоторую комбинацию из массы и ее расстояний до оси вращения. Подобная характеристика была найдена – это так называемый момент инерции I. В простейших случаях он является числовой величиной, как и масса (т.е. это не вектор).

В частности, у шарика массой m на невесомой нити – момент инерции , где r – длина нити. Для двух разных шариков; соединенных невесомой спицей, рассматриваемых как модель двухатомной молекулы типа NaCl, момент инерции , т.е. зависит от масс шариков и их расстояний до оси вращения.

Фундаментальной характеристикой, аддитивной и сохраняющейся для изолированной системы при вращении, является вектор J, называемый полным моментом. В частном случае вращения системы вокруг определенной оси и направлен вдоль оси вращения. Соответственно, кинетическая энергия вращения в этом случае равна .

Для изолированной системы из постоянства импульса системы следует постоянство ее скорости, ибо масса постоянна сама по себе. В то же время никаких требований типа постоянства момента инерции изолированной системы в природе не существует. Поэтому при постоянном полном моменте угловая скорость системы может меняться как по величине, так и по направлению, что находит отражение в наблюдаемых неожиданных свойствах вращательного движения (вспомним, как увеличивается скорость вращения фигуриста, когда он резко прижимает руки к телу). Далее, при поступательном движении изолированной системы все частицы движутся по прямым, параллельным вектору импульса. В то же время при вращении вокруг оси все частицы такой системы движутся в параллельных плоскостях, перпендикулярных вектору полного момента.

Полный момент скорее напоминает полную энергию, чем импульс. Если система как целое покоится (т.е. ее импульс равен нулю), но она совершает вращение, полный момент системы отличен от нуля. В этом случае он называется собственным моментом S (аналог энергии покоя). Если одновременно с вращением система движется как целое, то полный момент можно представить в виде

J = S + L (6.7),

где L – называется орбитальным моментом (аналог кинетической энергии).