
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 3.2. Шифры замены.
Шифрами замены называются такие шифры, преобразования из которых приводят к замене каждого символа открытого текста на другие символы – шифрообозначения, причем порядок следования шифрообозначений совпадает с порядком следования соответствующих им символов открытого сообщения.
В своей простейшей форме шифр замены может быть задан таблицей подстановки, устанавливающей соответствие между буквами двух алфавитов An и Bn:
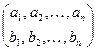 ,
,
где 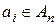 – i-тая буква алфавита открытого текста,
– i-тая буква алфавита открытого текста, 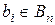 – шифрообозначение ai (соответствующая ai буква алфавита шифртекста).
– шифрообозначение ai (соответствующая ai буква алфавита шифртекста).
В качестве примера преобразования, которое может содержаться в шифре замены, приведем такое правило. Каждая буква исходного сообщения заменяется на ее порядковый номер в алфавите. В этом случае исходный буквенный текст преобразуется в числовой.
Алфавиты An и Bn не обязательно должны быть различными. В практической криптографии очень часто применяются шифры, в которых алфавиты An и Bn совпадают.
В шифре простой замены каждый символ исходного текста заменяется символами того же алфавита одинаково на всем протяжении текста.
В шифрах сложной замены для шифрования каждого символа открытого текста применяют свой шифр простой замены. Для реализации шифров сложной замены последовательно и циклически меняют используемые таблицы подстановки.
Полибианский квадрат.Одним из первых шифров простой замены считается так называемый полибианский квадрат. За два века до нашей эры греческий писатель и историк Полибий изобрел для целей шифрования квадратную таблицу размером 5x5, заполненную буквами греческого алфавита в случайном порядке (рис. 1.7).

Рис. 1.7. Полибианский квадрат
При шифровании в этом полибианском квадрате находили очередную букву открытого текста и записывали в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста оказывалась в нижней строке таблицы, то для шифртекста брали самую верхнюю букву из того же столбца. Например, для слова "tauros" получается шифртекст "Cjdmtx".
Концепция полибианского квадрата оказалась плодотворной и нашла применение в криптосистемах последующего времени.
Система шифрования Цезаря.Шифр Цезаря является частным случаем шифра простой замены. Свое название этот шифр получил по имени римского императора Гая Юлия Цезаря, который использовал этот шифр при переписке с Цицероном (около 50 г. до н.э.).
При шифровании исходного текста каждая буква заменялась на другую букву того же алфавита по следующему правилу. Заменяющая буква определялась путем смещения по алфавиту от исходной буквы на К букв. При достижении конца алфавита выполнялся циклический переход к его началу. Цезарь использовал шифр замены при смещении К = 3. Такой шифр замены можно задать таблицей подстановки, содержащей соответствующие пары букв открытого текста и шифртекста. Совокупность возможных подстановок для К=3 показана в табл. 1.1.
Таблица 1.1.
Таблица подстановкИ шифра Цезаря
A®D J®M S®V
B®E K®N T®W
C®F L®O U®X
D®G M®P V®Y
E®H N®Q W®Z
F®I O®R X®A
G®J P®S Y®B
H®K Q®T Z®C
I®L R®U
Например, послание Цезаря "VENI VIDI VICI" ("Пришел, Увидел, Победил") выглядело бы в зашифрованном виде так: "YHQL YLGL YLFL".
Система шифрования Цезаря с ключевым словом. Особенностью этой системы является использование ключевого слова для смещения и изменения порядка символов в алфавите подстановки.
Выберем некоторое число k, 0 < k < 25 , и слово или короткую фразу в качестве ключевого слова. Желательно, чтобы все буквы ключевого слова были различными. Пусть выбраны слово DIPLOMAT в качестве ключевого слова и число k= 5.
Ключевое слово записывается под буквами алфавита, начиная с буквы, числовой код которой совпадает с выбранным числом k:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| D | I | P | L | O | M | A | T |
Оставшиеся буквы алфавита подстановки записываются после ключевого слова в алфавитном порядке:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| V | W | X | Y | Z | D | I | P | L | O | M | A | T | B | C | E | F | G | H | J | K | N | Q | R | S | U |
Шифрующие таблицы Трисемуса. В 1508 г. аббат из Германии Иоганн Трисемус написал печатную работу по криптологии под названием "Полиграфия". В этой книге он впервые систематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра замены обычно использовались таблица для записи букв алфавита и ключевое слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку. Поскольку ключевое слово или фразу легко хранить в памяти, то такой подход упрощал процессы шифрования и расшифрования.
Поясним этот метод шифрования на примере. Для русского алфавита шифрующая таблица может иметь размер 4x8. Выберем в качестве ключа слово БАНДЕРОЛЬ. Шифрующая таблица с таким ключом показана на рис. 1.8.
| Б | А | Н | Д | Е | Р | О | Л |
| Ь | В | Г | Ж | З | И | Й | К |
| М | П | С | Т | У | Ф | Х | Ц |
| Ч | Ш | Щ | Ы | Ъ | Э | Ю | Я |
Рис. 1.8. Шифрующая таблица Трисемуса с ключевым словом "БАНДЕРОЛЬ"
Как и в случае полибианского квадрата, при шифровании находят в этой таблице очередную букву открытого текста и записывают в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста оказывается в нижней строке таблицы, тогда для шифртекста берут самую верхнюю букву из того же столбца.
Например, при шифровании с помощью этой таблицы сообщения "ВЫЛЕТАЕМПЯТОГО" получаем шифртекст "ПДКЗЫВЗЧШЛЫЙСЙ".
Система шифрования Вижинера впервые была опубликована в 1586 г. и является одной из старейших и наиболее известных шифров сложной замены. Свое название она получила по имени французского дипломата XVI века Блеза Вижинера, который развивал и совершенствовал криптографические системы.
Система Вижинера подобна такой системе шифрования Цезаря, у которой ключ подстановки меняется от буквы к букве. Этот шифр можно описать таблицей шифрования, называемой таблицей (квадратом) Вижинера. Пример квадрата Вижинера для русского языка приведен в табл. 1.2.
Таблица Вижинера используется для шифрования и расшифрования. Таблица имеет два входа: верхнюю строку подчеркнутых символов, используемую для считывания очередной буквы исходного открытого текста; крайний левый столбец ключа. Последовательность ключей обычно получают из числовых значений букв ключевого слова.
При шифровании исходного сообщения его выписывают в строку, а под ним записывают ключевое слово (или фразу). Если ключ оказался короче сообщения, то его циклически повторяют. В процессе шифрования находят в верхней строке таблицы очередную букву исходного текста и в левом столбце очередное значение ключа. Очередная буква шифртекста находится на пересечении столбца, определяемого шифруемой буквой, и строки, определяемой числовым значением ключа.
Рассмотрим пример получения шифртекста с помощью таблицы Вижинера. Пусть выбрано ключевое слово "АМБРОЗИЯ". Необходимо зашифровать сообщение "ПРИЛЕТАЮ СЕДЬМОГО".
Выпишем исходное сообщение в строку и запишем под ним ключевое слово с повторением. В третью строку будем выписывать буквы шифртекста, определяемые из таблицы Вижинера.
Сообщение ПРИЛЕТАЮ СЕДЬМОГО
Ключ АМБРОЗИЯ АМБРОЗИЯ
Шифртекст ПЪЙЫУЩИЭ ССЕКЬХЛН
Таблица 1.2.
Дата добавления: 2014-12-23; просмотров: 371; Мы поможем в написании вашей работы!; Нарушение авторских прав |