Аналитического преобразования.

Суть этого метода состоит в том, что символы шифруемого текста последовательно складываются с символами некоторой специальной последовательности, которая называется гаммой. Иногда такой метод представляют как наложение гаммы на исходный текст, поэтому он получил название «гаммирование».

Процедуру наложения гаммы на исходный текст можно осуществить двумя способами. При первом способе символы исходного текста и гаммы заменяются цифровыми эквивалентами, которые затем складываются по модулю k, где k — число символов в алфавите, т. е.

Ri = (Si + G) mod (k — 1), где Ri, Si, G — символы соответственно зашифрованного, исходного

текста и гаммы.

При втором методе символы исходного текста и гаммы представляются в виде двоичного кода, затем соответствующие разряды складываются по модулю 2. Вместо сложения по модулю 2 при гам-мировании можно использовать и другие логические операции, например преобразование по правилу логической эквивалентности или логической неэквивалентности.

Такая замена равносильна введению еще одного ключа, которым является выбор правила формирования символов зашифрованного сообщения из символов исходного текста и гаммы. Стойкость шифрования методом гаммирования определяется главным образом свойствами гаммы — длительностью периода и 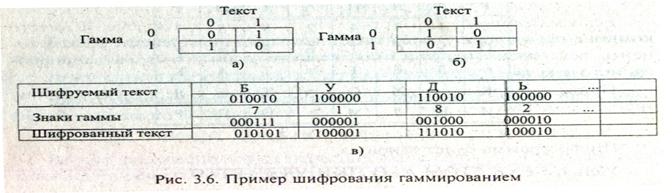равномерностью статистических характеристик. Последнее свойство обеспечивает отсутствие закономерностей в появлении различных символов в пределах периода.

Обычно разделяют две разновидности гаммирования — с конечной и бесконечной гаммами. При хороших статистических свойствах гаммы стойкость шифрования определяется только длиной периода гаммы. При этом, если длина периода гаммы превышает длину шифруемого текста, то такой' шифр теоретически является абсолютно стойким, т. е. его нельзя вскрыть при помощи статистической обработки зашифрованного текста. Это, однако, не означает, что дешифрование такого текста вообще невозможно: при наличии некоторой дополнительной информации исходный текст может быть частично или полностью восстановлен даже при использовании бесконечной гаммы.

В качестве гаммы может быть использована любая последовательность случайных символов, например последовательность цифр числа а, числа е (основание натурального логарифма) и т. п. При шифровании с помощью ЭВМ последовательность гаммы может формироваться с помощью датчика псевдослучайных чисел (ПСЧ). В настоящее время разработано несколько алгоритмов работы таких датчиков, которые обеспечивают удовлетворительные характеристики гаммы.