
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные аксиомы и законы алгебры логики
| Тождество | Название | Примечание | ||
| а б | А+0=А А*1=А | Закон сложения с нулем Закон умножения на единицу | выражения 1-5 это АКСИОМЫ | |
| а б | А+1=1 А*0=0 | Закон сложения с единицей Закон умножения на ноль | ||
| а б | А+А=А А*А=А | Законы тождественности | ||
| а б | (Х)=х=х | Закон отрицания Закон двойного отрицания | ||
| а б | А+А=1 А*А=0 | Закон исключенного третьего Закон противоречия | ||
| а б | А+В=В+А А*В=В*А | Закон коммутативности | Переместительный закон | |
| а б | А+В+С=А+(В+С) =(А+В)+С А*В*С=А*(В*С)= =(А*В)*С | Закон ассоциативности | Сочетательный закон | |
| а б | А+В*С=(А+В)(А+С) А(В+С)=А * В+А *С | Закон дистрибутивности сложения по отношению к умножению Закон дистрибутивности умножения по отношению к сложению | Распределительный закон. В обычной алгебре нег аналога. V | |
| а б | А+А*В=А+В А(А+В)=А*В | Следствие законов дистрибутивности | Теоремы 9-11 доказываются помощью предыдущих законов | |
| а б | А+А*В=А А(А+В)=А | Закон поглощения | ||
| а б | А*В+А*В=В (A+B)(А+B)=B | Закон склеивания | ||
| а б | А+В=А*В А*В=А+В | Закон дуальности (теорема де Моргана) | Справедливы для любого числа переменных, доказываются с помощью таблиц истинности |
Алгебраические выражения аксиом и законов заданы парами. При этом второе выражение получается из первого путем замены операции И , ИЛИ и символов 0,1.
Эквивалентные схемы резисторного каскада усиления
на различных частотах
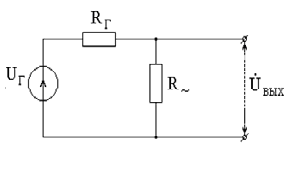
Рис. 4. Преобразованная и обобщенная эквивалентная схема резисторного каскада на средних частотах

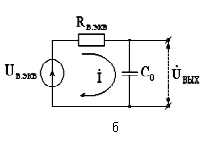
Рис. 5. Преобразованные и обобщенные эквивалентные схемы резисторного каскада усиления: а - на нижних частотах; б - на верхних частотах
Физическое объяснение вида частотной и фазовой характеристик резисторного каскада усиления


Дата добавления: 2014-12-23; просмотров: 332; Мы поможем в написании вашей работы!; Нарушение авторских прав |