
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 3. Магнитное поле. Закон Био-Савара-Лапласа
Электрический ток создает поле, действующее на магнитную стрелку. Стрелка ориентируется по касательной к окружности, лежащей в плоскости, перпендикуляной к проводнику с током (рис. 9).
Основной характеристикой магнитного поля является вектор индукция 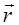 . Принято, что вектор индукция
. Принято, что вектор индукция 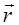 магнитного поля направлен в сторону север-ного полюса магнитной стрелки, помещенной в данную точку поля (рис. 9).
магнитного поля направлен в сторону север-ного полюса магнитной стрелки, помещенной в данную точку поля (рис. 9).
По аналогии с электрическим полем, магнитное поле также может быть изображено графически с помощью силовых линий (линий индукции магнитного поля).
Силовая линия – это такая линия, касательная к которой в каждой точке совпадает по направлению с вектором индукции 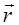 магнитного поля. Силовые линии магнитного поля, в отличие от силовых линий электростатического поля, являются замкнутыми и охватывают проводники с током. Направление силовых линий задается правилом правого винта (правилом буравчика): головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции (рис. 9).
магнитного поля. Силовые линии магнитного поля, в отличие от силовых линий электростатического поля, являются замкнутыми и охватывают проводники с током. Направление силовых линий задается правилом правого винта (правилом буравчика): головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции (рис. 9).

Рис. 9
Для нескольких источников магнитного поля согласно принципу суперпозиции магнитных полей индукция результирующего магнитного поля равна векторной сумме индукций всех отдельных магнитных полей:
 .
.
Вектор индукции 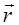 магнитного поля, создаваемого проводником с током
магнитного поля, создаваемого проводником с током  , можно определить с помощью закона Био-Савара-Лапласа.При этомнеобходимо учесть то, что закон Био-Савара-Лапласапозволяет найти модуль и направление лишьвектора индукции
, можно определить с помощью закона Био-Савара-Лапласа.При этомнеобходимо учесть то, что закон Био-Савара-Лапласапозволяет найти модуль и направление лишьвектора индукции  магнитного поля, создаваемого элементом проводника
магнитного поля, создаваемого элементом проводника 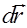 с током
с током  . Поэтому, для определения вектора индукции
. Поэтому, для определения вектора индукции 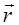 магнитного поля, создаваемого проводником с током
магнитного поля, создаваемого проводником с током  , необходимо первоначально разбить этот проводник на элементы проводника
, необходимо первоначально разбить этот проводник на элементы проводника 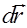 , для каждого элемента с помощью закона Био-Савара-Лапласа найти вектор индукции
, для каждого элемента с помощью закона Био-Савара-Лапласа найти вектор индукции  , а затем, используя принцип суперпозиции магнитных полей, сложить векторно все найденные вектора индукции
, а затем, используя принцип суперпозиции магнитных полей, сложить векторно все найденные вектора индукции  .
.
Закон Био-Савара-Лапласав векторной форме:

 ,
,
где  – индукция магнитного поля в точке M, заданной радиусом-вектором
– индукция магнитного поля в точке M, заданной радиусом-вектором  , проведенным от начала вектора
, проведенным от начала вектора  до этой точки;
до этой точки;
 – векторное произведение векторов
– векторное произведение векторов 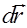 и
и  ;
;
 – магнитная постоянная,
– магнитная постоянная,
 – магнитная проницаемость среды.
– магнитная проницаемость среды.
Направление вектора  определяется по правилу правого винта: направление вращения головки винта дает направление вектора
определяется по правилу правого винта: направление вращения головки винта дает направление вектора  , если поступательное движение винта совпадает с направлением тока в элементе проводника (рис. 10).
, если поступательное движение винта совпадает с направлением тока в элементе проводника (рис. 10).
В скалярном виде закон Био-Савара-Лапласа:
 , где
, где  – угол между векторами
– угол между векторами  и
и 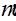 .
.
Магнитное поле линейного тока.Для нахождения индукции 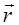 магнитного поля, созданного прямым проводником с током (рис. 11), необходимо разбить весь проводник на элементы
магнитного поля, созданного прямым проводником с током (рис. 11), необходимо разбить весь проводник на элементы  , для каждого элемента проводника
, для каждого элемента проводника  с током I найти вектор индукции
с током I найти вектор индукции  , а затем векторно сложить все найденные
, а затем векторно сложить все найденные  .
.
В произвольной точке М, удаленной от оси проводника на расстояние b (рис. 11), векторы  от всех элементов проводника
от всех элементов проводника  с током I имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов
с током I имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов  можно заменить сложением их модулей.
можно заменить сложением их модулей.

По закону Био-Савара-Лапласа модуль вектора магнитной индукции  в точке М поля, созданного элементом проводника
в точке М поля, созданного элементом проводника  с током I :
с током I :
 .
.
В качестве переменной интегрирования выберем угол  , выразив через этот угол все остальные величины.
, выразив через этот угол все остальные величины.
Из рисунка 11 следует, что 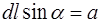 , а с другой стороны,
, а с другой стороны,  .
.
Тогда  , а модуль вектора магнитной индукции
, а модуль вектора магнитной индукции  в точке М :
в точке М :
 .
.
Из прямоугольного треугольника DOM :
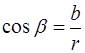 , откуда
, откуда  .
.
Следовательно, индукция dB, создаваемая элементом проводника dl с током I :
 .
.
Теперь можно перейти к интегрированию:
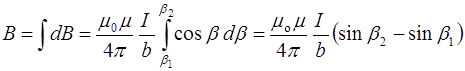 .
.
Так как угол  для прямого тока изменяется в пределах от
для прямого тока изменяется в пределах от  до
до  , то магнитная индукция поля прямого тока:
, то магнитная индукция поля прямого тока:
 .
.
Следовательно,
 .
.
Магнитное поле в центре кругового проводника с током. Для нахождения индукции магнитного поля в центре кругового проводника с током необходимо разбить этот проводник на элементы  , причем все элементы проводника с током создают в центре кругового тока магнитные поля одинакового направления – вдоль нормали к плоскости витка (рис. 12).
, причем все элементы проводника с током создают в центре кругового тока магнитные поля одинакового направления – вдоль нормали к плоскости витка (рис. 12).  Поэтому сложение векторов
Поэтому сложение векторов  можно заменить сложением их модулей dB.
можно заменить сложением их модулей dB.
По закону Био-Савара-Лапласа модуль вектора  :
:
 .
.
Так как все элементы  проводника перпендикулярны соответствующим радиусам-векторам
проводника перпендикулярны соответствующим радиусам-векторам  (рис. 12), то sina = 1 для всех элементов
(рис. 12), то sina = 1 для всех элементов  . Расстояния r для всех элементов проводника
. Расстояния r для всех элементов проводника  также одинаковые (r = R).
также одинаковые (r = R).
Тогда выражение для модуля вектора  примет вид:
примет вид:
 .
.
Теперь для нахождения модуля вектора  можно перейти к интегрированию:
можно перейти к интегрированию:
 .
.
Следовательно, индукция магнитного поля B в центре кругового проводника радиусом R с током I :
 .
.
Тема 4. Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца)
Закон Ампера. На элемент проводника  с током I , помещённый в магнитное поле с индукцией
с током I , помещённый в магнитное поле с индукцией 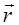 действует сила
действует сила  (
(  – сила Ампера):
– сила Ампера):  .
.
 Модуль вектора
Модуль вектора  :
:  ,
,
где  – угол между векторами
– угол между векторами  и
и 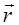 .
.
Направление вектора  можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление силы Ампера(рис. 13, сила
можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление силы Ампера(рис. 13, сила  перпендикулярна плоскости рисунка).
перпендикулярна плоскости рисунка).
 Сила Лоренца. На заряд q , движущийся со скоростью
Сила Лоренца. На заряд q , движущийся со скоростью 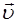 в магнитном поле с индукцией
в магнитном поле с индукцией 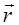 , действует сила
, действует сила  (
(  – сила Лоренца ):
– сила Лоренца ):  .
.
Модуль вектора  :
:  ,
,
где α – угол между векторами 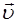 и
и 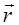 .
.
 Направление вектора
Направление вектора  может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов: если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис.14, сила
может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов: если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис.14, сила  перпендикулярна плоскости рисунка).
перпендикулярна плоскости рисунка).
Дата добавления: 2014-12-23; просмотров: 458; Мы поможем в написании вашей работы!; Нарушение авторских прав |