Гидравлическая сеть
Один и тот же насос может работать с различными гидравлическими сетями, как показано на Рис.10.
Иллюстрация включения насоса в различные гидравлические сети
Рис.10
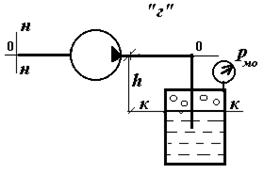
На схеме “а” насос поднимает жидкость на высоту h; на схеме “б” перемещает жидкость по горизонтальному трубопроводу; на схеме “в” поднимает жидкость в цилиндр, на поршень которого действует сила R; на схеме “г” перемещает жидкость в закрытый резервуар, расположенный ниже оси насоса с избыточным давлением на свободной поверхности.
Очевидно, что в разных схемах для перемещения жидкости требуется различная энергия (напор), в то же время зависимость напора насоса от подачи определяется его напорной характеристикой. Как же “совместить” интересы насоса и гидравлической сети? Для этого нужно определить рабочую точку насоса.
Рабочая точка насоса -это точка пересечения характеристики насоса с характеристикой гидравлической сети.
Характеристика гидравлической сети -зависимость удельной энергии (напора), необходимой для перемещения жидкости в данной системе, от расхода жидкости в ней.
Уравнение гидравлической сети выражает закон сохранения энергии для начального и конечного сечений гидравлической системы. Энергия, которую необходимо передать жидкости, записывается при этом в левую часть уравнения в виде потребного напора Hпотр.
Характеристику гидравлической сети часто называют кривой потребного напора.
Для любой насосной трубопроводной системы закон сохранения энергии имеет вид:
|
| eн + Hпотр = eк + hн-к ,
| (16)
| где eн - удельная (на единицу веса) энергия жидкости в начальном сечении н-н , eк - удельная (на единицу веса) энергия жидкости в конечном сечении к-к , Hпотр- потребный напор насоса, а hн-к - потери удельной энергии на преодоление гидравлических сопротивлений.
Чтобы получить уравнение гидравлической сети, необходимо:
1. Выбрать сечения для составления уравнения сети (16) и горизонтальную плоскость О - О отсчета величин z, которую удобно совместить с начальным сечением.
2.Записать закон сохранения энергии (16), раскрывая содержание энергий eн и eк по уравнению Бернулли:
|
| 
|
(17)
| 3. Из уравнения (17) определить потребный напор насоса:
|
| 
|
(18)
| 4. Раскрыть содержание слагаемых уравнения (18) для данной гидравлической системы. Здесь:
zн, pн, Jн- соответственно вертикальная отметка относительно плоскости 0-0, абсолютное давление и средняя скорость в начальном сечении потока, а zк, pк, Jк -то же в конечном сечении. Если сечение расположено ниже плоскости 0-0, отметка z берется со знаком минус.
Потери энергии hн-к представляют собой сумму потерь энергии на трение по длине и местных гидравлических сопротивлений:
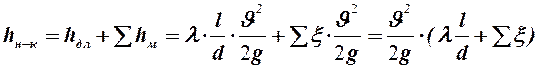
|
(19)
| где J- скорость движения жидкости в трубопроводе, коэффициенты местных сопротивлений xi определяются по справочным данным, а коэффициент гидравлического трения l по следующим формулам:
| l=64/Re
| - ламинарный режим
| (20)
| | l=0,11(68/Re+Dэ/d)0,25
| - турбулентный режим
| (21)
| Формулы (20) и (21) приведены для ньютоновской жидкости. Более подробно об определении потерь энергии будет сказано в разделе 1.3.
5. Выразить в уравнениях (18), (19), (20) и (21) скорости движения и число Re через расход жидкости:
|
| Jн=Q/wн , Jк=Q/wк , J=Q/wтр, Re=4Q/pdn,
| (22)
| где wн , wк, wтр - площади соответствующих сечений потока, d- диаметр трубопровода, а n- кинематический коэффициент вязкости жидкости.
Результат выполнения пунктов 4 и 5, например, для схемы Рис.10”а” имеет вид:
 . .
|
(23)
| 6. Анализируем уравнение (23). Поскольку площади начального и конечного сечений много больше площади сечения трубопровода, первыми двумя слагаемыми в скобках уравнения (23) можно пренебречь. Тогда:

|
(24)
| 7. Изображаем уравнение сети (24) на том же графике, что и напорная характеристика насоса и находим точку их пересечения.
Для построения характеристики сети задаемся значениями расхода Q в диапазоне подач насоса, начиная от нуля, подставляем эти значения в уравнение (24) и определяем H. При решении задачи в общем виде (без численных значений), характеристику сети проводим качественно, по виду функции (24).
   
Рис.11
В нашем случае при Q=0, H=h (допустим 40м, Рис.11). Далее, при увеличении расхода Q до Qкр имеет место ламинарный режим движения в трубе, коэффициент трения l обратно пропорционален расходу ( определяется по формуле (20)). При этом в уравнении (24) первое слагаемое справа (h)- постоянно, второе слагаемое (потери по длине) пропорционально Q в первой степени, в третье слагаемое (местные потери) пропорционально Q2. В итоге характеристика сети имеет вид параболы.
 
На пересечении характеристик насоса и сети определяется точка, в которой напор насоса равен потребному. Это и есть рабочая точка насоса в данной гидравлической сети. Её координаты - Hн и Qн.
При подаче Qн на кривой к.п.д. определяется коэффициент полезного действия насоса, и далее, из формулы (8) мощность на валу насоса, по которой подбирается приводной двигатель.
На Рис.12 показаны характеристики гидравлических сетей, изображенных на Рис.10. Уравнения сетей имеют вид:
| Сеть
| Уравнение
| Величина сi
| | а
|  . .
|
h
| |
б
|  . .
|
| | в
|

|

| | г
| 
|

|                 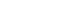   
Рис.12.
Анализ показывает, что при ламинарном режиме движения жидкости в трубопроводе и при отсутствии местных гидравлических сопротивлений (сеть”б”, Рис.10), характеристика сети представляет собой прямую линию (линия “б”, Рис.12).
Точка пересечения характеристики сети с осью абсцисс (точка С, линия г) определяет расход при движении жидкости самотеком, то есть за счет разности геометрических высот h (сеть “г”, Рис.10).
|






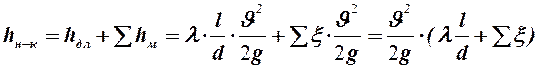
 .
.







 .
.
 .
.