Пример 1. Имеются данные о производительности труда и фондовооруженности нескольких предприятий (таблица 2)

Имеются данные о производительности труда и фондовооруженности нескольких предприятий (таблица 2). Провести корреляционно-регрессионный анализ влияния фондовооруженности на производительность труда.

В качестве факторного признака x выступит фондовооруженность труда, результативного y – производительность труда.

Данные в таблице 3 (графы 2,3) представлены после предварительной их обработки методом сопоставления двух параллельных рядов. Остальные графы таблицы используются как промежуточные расчеты.

Таблица 3

Расчетные данные

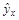
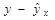
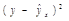
№п/п	x	y	x2	yx				y2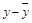
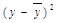
	2,74	3,78	7,5076	10,3572	6,7412	-2,9612	8,7687	14,2884	-4,35	18,8912
	3,10	6,48	9,6100	20,0880	6,8780	-0,3980	0,1584	41,9904	-1,65	2,7106
	3,49	5,61	12,1801	19,5789	7,0262	-1,4162	2,0056	31,4721	-2,52	6,3323
	4,02	10,02	16,1604	40,2804	7,2276	2,7924	7,7975	100,4004	1,89	3,5857
	4,12	7,24	16,9744	29,8288	7,2656	-0,0256	0,0007	52,4176	-0,89	0,7857
	4,19	5,59	17,5561	23,4221	7,2922	-1,7022	2,8975	31,2481	-2,54	6,4333
	4,30	18,00	18,4900	77,4000	7,3340	10,6660	113,7636	324,0000	9,87	97,4880
	4,66	5,22	21,7156	24,3252	7,4708	-2,2508	5,0661	27,2484	-2,91	8,4472
	4,80	6,69	23,0400	32,1120	7,5240	-0,8340	0,6956	44,7561	-1,44	2,0632
	5,01	9,42	25,1001	47,1942	7,6038	1,8162	3,2986	88,7364	1,29	1,6734
	5,01	6,57	25,1001	32,9157	7,6038	-1,0338	1,0687	43,1649	-1,56	2,4224
	5,10	5,39	26,0100	27,4890	7,6380	-2,2480	5,0535	29,0521	-2,74	7,4879
	5,23	8,16	27,3529	42,6768	7,6874	0,4726	0,2234	66,5856	0,03	0,0011
	5,65	7,65	31,9225	43,2225	7,8470	-0,1970	0,0388	58,5225	-0,48	0,2270
	5,82	6,70	33,8724	38,9940	7,9116	-1,2116	1,4680	44,8900	-1,43	2,0346
	5,91	7,00	34,9281	41,3700	7,9458	-0,9458	0,8945	49,0000	-1,13	1,2688
	6,52	11,03	42,5104	71,9156	8,1776	2,8524	8,1362	121,6609	2,90	8,4309
	6,67	8,77	44,4889	58,4959	8,2346	0,5354	0,2867	76,9129	0,64	0,4142
	7,67	4,23	58,8289	32,4441	8,6146	-4,3846	19,2247	17,8929	-3,90	15,1819
	8,30	9,02	68,8900	74,8660	8,8540	0,1660	0,0276	81,3604	0,89	0,7985
	8,94	9,27	79,9236	82,8738	9,0972	0,1728	0,0299	85,9329	1,14	1,3078
	10,44	10,44	108,9936	108,9936	9,6672	0,7728	0,5972	108,9936	2,31	5,3527
	11,44	6,54	130,8736	74,8176	10,0472	-3,5072	12,3005	42,7716	-1,59	2,5167
	11,63	13,28	135,2569	154,4464	10,1194	3,1606	9,9894	176,3584	5,15	26,5596
	11,99	11,06	143,7601	132,6094	10,2562	0,8038	0,6461	122,3236	2,93	8,6060
Итого	156,75	203,16	1161,0463	1342,7172	202,0650		204,4372	1881,9802		231,0208
В среднем	6,27	8,13	46,4419	53,7087	8,0826		8,1775	75,2792		9,2408

Проведем визуальный анализ данных путем построения корреляционного поля зависимости производительности труда от фондовооруженности.

Рисунок 1 – Корреляционное поле зависимости производительности труда от фондовооруженности

Проанализировав данные и их графическое изображение, можно сделать предположение, что связь между признаками линейная и она описывается уравнением прямой (1): .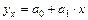

Определим параметры уравнения прямой на основе метода наименьших квадратов, решив систему нормальных уравнений (9).

По формулам (10), (11) вычислим а₀, а₁, используя расчетные данные таблицы 3:

,

.

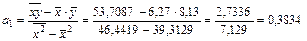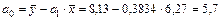Вычислив параметры, получим следующее уравнение:

.

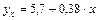Следовательно, с увеличением фондовооруженности на 1 тыс. рублей, производительность труда увеличится на 0,3834 тыс. рублей.

Значимость коэффициентов регрессии проверим по t – критерию Стьюдента. Вычислим расчетные значения t – критерия по формулам (12)-(16):

,

;

;

.

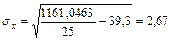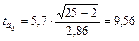Вычисленные значения сравниваем с критическим t по таблице Стьюдента (приложение А) с учетом уровня значимости a = 0,05 и числом степеней свободы n = n-k-1 = 25-1-1 = 23.

Т.к. больше t_табл=2,069, параметр а₀ признается значимым, т.е. в этом случае практически невероятно, что найденное значение параметра обусловлено только случайными совпадениями; 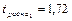меньше t_табл=2,069, следовательно, параметр а₁ признается незначимым.

Выявим тесноту корреляционной связи между x и y с помощью линейного коэффициента корреляции, используя формулу (20):

.

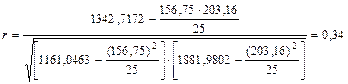Т.к. r =0,34, то связь прямая, слабая.

Значимость линейного коэффициента корреляции определяется по формуле (21) с помощью t – критерия Стьюдента (число степеней свободы ν=23, уровень значимости α=0,05):

.

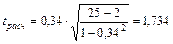Т.к t_расч=1,734 меньше t_табл=2,069, следовательно, коэффициент корреляции признается незначимым.

Определим линейный коэффициент детерминации r²:

.

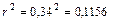Он показывает, что 11,56% вариации производительности труда обусловлено вариацией фондовооруженности.

Теоретическое корреляционное отношение h определим по формуле (19):

.

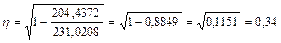Т.к. 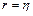, то будем считать, что линейная форма связи между y и x₁ выбрана верно.

Экономическую интерпретацию модели дополнит коэффициент эластичности:

.

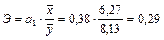Это значит, что при увеличении фондовооруженности труда на 1% производительность труда возрастет на 0,3%.