Реал газы. Уравнение Ван-дер-Ваальса. Изотермы реальных газов.

Реальный газ – газ, где учитываются объем (размеры) и силы взаимодействия молекул. Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И.Ван-дер-Ваальс введя поправки в уравнение Менделеева-Клайперона, вывел уравнение состояния реального газа:

1. Учет собственного объема молекул. Наличие сил отталкивания, которые проти­водействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не V_m, а V_m — b, где b — объем,занимаемый самими молекулами.

Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в рас­чете на одну молекулу.

2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислени­ям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату моляр­ного объема, т. е. , где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного при­тяжения, V_m — молярный объем.

Вводя эти поправки, получимуравнение Ван-дер-Ваальса для моля газа(уравнение состояния реальных газов):

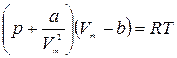
Для произвольного количества вещества v газа (v=m/M) с учетом того, что V=vV_m, уравнение Ван-дер-Ваальса примет вид

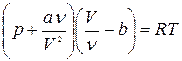
Изотермы Ван-дер-Ваальса - кривые зависимости р от V_m при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые имеют довольно своеобразный характер. При высоких температурах (T > T_к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре T_к на изотерме имеется лишь одна точка перегиба К.

Эта изотерма называется критической, соответствующая ей температура T_к — крити­ческой температурой; точка перегиба Кназывается критической точкой (точка в которой исчезают различия между жидкостью и газом); в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V_к, и давление р_к называются также критическими. Состояние с критическими парамет­рами (p_к, V_к, T_к) называется критическим состоянием. При низких температурах (Т < T_к ) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.

Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса к виду

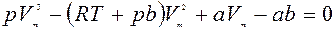
Уравнение при заданных р и Т является уравнением третьей степени относительно V_m; следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа V₁, V₂ иV₃ отвечают (символ «m» для простоты опускаем) одному значению давления р₁), второму случаю — изотермы при высоких температурах.

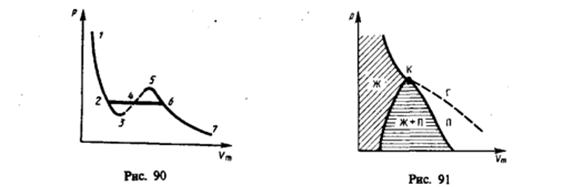
Рассматривая различные участки изотермы при T<Т_к (рис. 90), видим, что на участках 1—3 и 5—7 при уменьшении объема V_m давление р возрастает, что естественно. На участке 3 - 5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7—6—2—1. Часть 6–7 отвечает газообразному состоянию, а часть 2–1 - жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.

Для нахождения критических параметров подставим их значения в уравнение

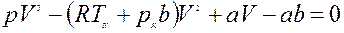
(символ «m» для простоты опускаем). Поскольку в критической точке все три корня совпадают и равны V_к уравнение приводится к виду

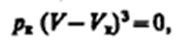или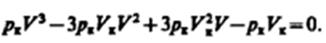

Tax как уравнения тождественны, то в них должны быть равны и коэффициенты при неизвестных соответствующих степеней. Поэтому можно записать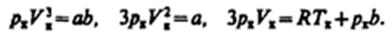

Решая полученные уравнения, найдем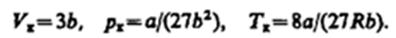

Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис. 91), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму р,V_m под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа — область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.